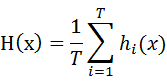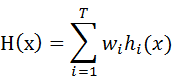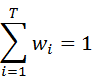随机森林算法梳理

一、集成学习概念：

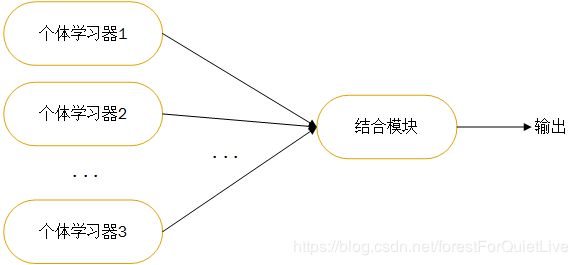
集成学习（ensemble learning）通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统（multi-classifier system）。集成学习将个体学习器采用某种策略结合。个体学习器通常由现有的学习算法从训练数据产生。如决策树、BP神经网络等。

集成中只包含同一种个体学习器叫做同质集成（homogeneous ensemble）；集成中的个体学习器由不同学习算法生成，叫做异质集成。

1.分类器之间应该有差异性；

2.每个分类器的精度必须大于0.5；

如果使用的分类器没有差异，那么集成起来的分类结果是没有变化的。分类器的精度p<0.5，随着集成规模的增加，分类精度不断下降；如果精度大于p>0.5，那么最终分类精度可以趋向于1。

二、个体学习器的概念：使用简单的学习算法对数据训练产生的，如决策树算法、神经网络算法等。

三、boosting算法指将弱学习算法组合成强学习算法，它的思想起源于Valiant提出的PAC(Probably Approximately Correct)学习模型。

基本思想：

1.首先赋予每个训练样本相同的初始化权重，在此训练样本分布下训练出一个弱分类器；

2.利用该弱分类器更新每个样本的权重，分类错误的样本认为是分类困难样本，权重增加，反之权重降低，得到一个新的样本分布；

3.在新的样本分布下，在训练一个新的弱分类器，并且更新样本权重，重复以上过程T次，得到T个弱分类器。

通过改变样本分布，使得分类器聚集在那些很难分的样本上，对那些容易错分的数据加强学习，增加错分数据的权重。这样错分的数据再下一轮的迭代就有更大的作用（对错分数据进行惩罚）。

bagging:给定包含m个样本的数据集，我们做有放回抽样（即自助采样法 bootstrap sampling），经过m次随机采样得到m个样本的采样集。这样我们可以采样出T个含m个训练样本的采样集。基于每个采样集训练出一个基学习器，对这些基学习器进行组合。

可以做一个简单的估计，样本在m次采样中始终不被采到的概率是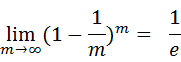： ，近似等于36.8%。这些样本可以作为验证集来对泛化性能进行“包外估计”。为此需要记录每个基分类器所使用的训练样本。

四、集合策略

1.平均法

• 简单平均法           

  

• 加权平均法

  

  其中，是个体学习器 的权重，通常要求 ，

2.投票法

• 绝对多数投票法（majority voting）若某标记得数过半，则预测为该标记；否则，拒绝预测。
• 相对多数投票法（plurality voting）若同时有多个标记获得最高票，则从中随机选取一个。
• 加权投票法（weighted voting）与加权平均法类似。每个弱学习器乘上一个权重参数。

3.学习法

  在stacking方法中，我们把个体学习器叫做初级学习器，用于结合的学习器叫做次级学习器或元学习器（meta-learner），次级学习器用于训练的数据叫做次级训练集。次级训练集是在训练集上用初级学习器得到的。

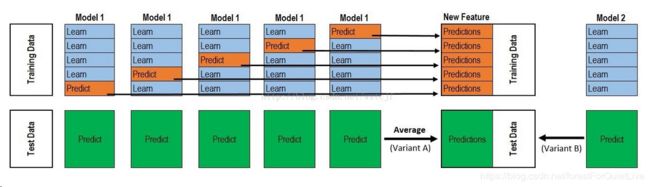
下面对这幅图进行解释：

假设训练数据有1万条，测试数据2500条。

1、对训练集进行5折交叉验证，每次8000训练（上图蓝色块），2000验证（上图橙色块）

2、每次验证相当于使用8000数据进行训练初级学习器，使用模型对验证集预测得到结果【2000 row,1 column】，得到测试结果

【2500 row,1 column】 。进行5折交叉验证后，验证集预测结果【2000*5 row,1 column】（标记为A1）,测试集结果5个【2500 row,1 column】，对5次结果进行平均得到【2500,1】（标记为B1）。

3、上面一个基学习器在数据集上预测结果为A1，B1；这样当我们对3个基模型进行集成的话，相于得到了A1、A2、A3、B1、B2、B3六个矩阵。

之后我们会将A1、A2、A3并列在一起成10000行3列的矩阵作为training data,B1、B2、B3合并在一起成2500行3列的矩阵作为testing  data，让次级学习器基于这样的数据进行再训练。

再训练是基于每个基础模型的预测结果作为特征（三个特征），次级学习器会学习训练在多个基学习的预测结果上赋予权重w，使得最后的预测最为准确。

Blending与Stacking大致相同，只是Blending的主要区别在于训练集不是通过K-Fold的CV策略来获得预测值，生成第二阶段模型的特征，而是建立一个Holdout集，例如10%的训练数据，第二阶段的次级学习器基于第一阶段模型对这10%训练数据的预测值进行拟合。

Stacking和Blending的优缺点对比

	优点	缺点
Stacking	1.方式简单 2..避开了一个信息泄露问题：generlizers和stacker使用了不一样的数据集 3.在团队建模过程中，不需要给队友分享自己的随机种子	使用了很少的数据,可能会过拟合
Blending	使用多次的CV会比较稳健	容易导致信息泄露

mlxtend库对stacking进行实现，可以方便的进行stacking。

五、随机森林思想

随机森林（Random Forest）在以CART决策树为弱学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。

特征随机性是指：在生成每棵树的时候，每个树选取的特征都仅仅是随机选出的少数特征，一般默认取特征总数m的开方。而一般的CART树则是会选取全部的特征进行建模。因此，保证了特征随机性。

六、随机森林的推广

"ExtraTreesClassifier"
"ExtraTreesRegressor"
"RandomTreesEmbedding"

七、优缺点

• 在测试集上表现良好，两个随机性的引入，使得随机森林不容易陷入过拟合（样本随机，特征随机）
• 由于树的组合，使得随机森林可以处理非线性数据，本身属于非线性分类（拟合）模型
• 它能够处理很高维度（feature很多）的数据，并且不用做特征选择，对数据集的适应能力强：既能处理离散型数据，也能处理连续型数据，数据集无需规范化
• 训练速度快，可以运用在大规模数据集上
• 可以处理缺省值（单独作为一类），不用额外处理
• 由于有袋外数据（OOB），可以在模型生成过程中取得真实误差的无偏估计，且不损失训练数据量
• 在训练过程中，能够检测到feature间的互相影响，特征筛选且可以得出feature的重要性，具有一定参考意义
• 由于每棵树可以独立、同时生成，容易做成并行化方法
• 由于实现简单、精度高、抗过拟合能力强，当面对非线性数据时，适于作为基准模型

缺点：

• 随机森林在解决回归问题时，并没有像它在分类中表现的那么好，这是因为它并不能给出一个连续的输出。当进行回归时，随机森林不能够做出超越训练集数据范围的预测，这可能导致在某些特定噪声的数据进行建模时出现过度拟合。（PS:随机森林已经被证明在某些噪音较大的分类或者回归问题上回过拟合）
• 对于小数据或者低维数据（特征较少的数据），可能不能产生很好的分类。

八、sklearn参数

RF重要的Bagging框架的参数，由于RandomForestClassifier和RandomForestRegressor参数绝大部分相同。

parameter	含义
n_estimators	最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，计算量会太大，并且n_estimators到一定的数量后，再增大n_estimators获得的模型提升会很小，所以一般选择一个适中的数值。version0.20默认10，version0.02默认是100。
oob_score	是否采用袋外估计。default：False
criterion	树划分对特征的评价标注。default:gini,也可选entropy； 回归的话采用MSE或者MAE(平均绝对误差)

RF决策树参数：

参数	含义
max_depth	决策树最大深度。default:None(即对树深度不做限制)。 数据和特征较少时可以不考虑这个值。样本数量和特征数量较多时，推荐增加这个值。常用取值10~100.
max_features	划分时考虑的最大特征数。该属性取值较多。default：auto(即sqrt(n_features))，常用取值还有log2(n_features)。
min_samples_split	内部节点再划分所需最小样本数。default：2. 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。
min_samples_leaf	叶子节点最少样本数。默认是1.如果某叶子节点样本数目小于设定值，则会和兄弟节点一起被剪枝。样本数量级大时，推荐增大这个值。
min_weight_fraction_leaf	叶子节点最小的样本权重。default：0.就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
max_leaf_nodes	最大叶子节点数。通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。
min_impurity_split	节点划分最小不纯度。这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数，均方差)小于这个阈值，则该节点不再生成子节点。即为叶子节点 。一般不推荐改动默认值1e-7。

比较常用的参数为n_estimators、criterion、max_depth、max_features、min_samples_split、min_samples_leaf，其中min_samples_split和min_samples_leaf需要一起调参。

九、应用场景

数据维度相对低（几十维），同时对准确性有较高要求时。

参考链接：

随机森林优点参考：https://www.jianshu.com/p/a779f0686acc

随机森林缺点参考：https://blog.csdn.net/zhongjunlang/article/details/79488955

随机森林参数参考：https://scikit-learn.org和https://www.cnblogs.com/pinard/p/6160412.html

Stacking和Blending参考：https://blog.csdn.net/maqunfi/article/details/82220115

本文有些概念参考：周志华《机器学习》

https://mp.weixin.qq.com/s?__biz=MzAxMTU5Njg4NQ==&mid=100001388&idx=1&sn=21bae727bf3510fad98b3ec4a89d124e&chksm=1bbfe3562cc86a40769ea726f96e3a45185697f9582a2e3fbbbeec3af90dd722ebe09b635ddc