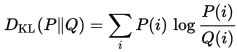吴军《数学之美》部分概念笔记（1-11章）

相关参考资料见正文

Good-turing模型：

由于我们是估算对于一个位置上出现单词wi的概率。这种情况下，在样本库中没有出现的单词，其概率并非为0. 但由于已有的Nr`r的累计和已经达到了1，所以必须采用一个“腾挪“的办法，将一部分的概率分布腾挪给未出现的单词。

解决办法就是在计算累计出现次数较少的单词时，将其概率替换为一个较小的值（此处的办法是将r替换为r‘）

　r^* = (r+1)*{n_{r+1}/n_r}

也就是说：这个变化默认认为：n_{r+1}/n_r这一下降速率显著的大于r+1/r的增长速率 

（因为在r-Nr符合Zipf定律）

http://www.52nlp.cn/mit-nlp-third-lesson-probabilistic-language-modeling-fifth-part

https://en.wikipedia.org/wiki/Zipf%27s_law

条件熵/互信息/相对熵/交叉熵：

都是基于引入特定字符可以获得多少信息量这样一个概念进行的定义

条件熵：H(X|Y) 

从信息论的角度消除不确定性： 与H(X)相比，引入Y后可以消除一定的不确定性。具体的不确定性即为条件熵（特定条件下的熵）

互信息：I(X,Y)=H(X)=H(X|Y) 关心不确定性的减少程度

所以，引入确定性(新 的制约条件Y)，则可以降低（或至少持平）整个系统的熵

相对熵/交叉熵：两个分布的差异性

------条件熵是两个变量的差异性而 相对熵是两个分布的差异性。

相对熵公式：

与前面的两个概念相比，相对熵/交叉熵关注的是一个数据的一组分布（一个足够大的数据量下的分布形态）下的熵

即某个数据的两种分布下，其熵的差值。

用信息论的方法表述：对指定的一组数据，用P(i)和Q(i)来拟合相应的数据的信息量。以P作为基准，衡量Q相对于P，表达这一组数据所需的信息量的差值。

如果P是理想最佳分布（例如严格按单词出现次数求和统计的p`log(p)）,Q是我们自己设计的一组分布情况。则评价Q的均衡性的办法，就是用Q(i)的信息长度去乘以P(i)，最后累加得到对理想P分布而言，Q分布的熵的差值（也就是和P相比有多大的差异性）

交叉熵公式是相对熵+E(p)：可认为是基于Q编码的总信息含量

https://www.zhihu.com/question/41252833

稀疏矩阵的快速计算方法

http://blog.csdn.net/lizhengjiang/article/details/40807061

http://www-users.cs.umn.edu/~saad/IterMethBook_2ndEd.pdf

TF-IDF：

TFIDF是：给定词汇，找出使这个词汇所能代表的信息量最大的文档。

可以理解为：

100篇文章均匀的分布了某单词（TF），与10篇文章均匀分布某单词的熵的差值（IDF修正）。

（此处前半句为全数据库统计采样结果，后半句为针对该单词的出现文章数量的一个权重修正）

这个概念是基于相对熵提出的。

即我先假定一个基础分布（完全平均P分布），此时某单词w的信息含量就是TF(w)log(TF(w))

而此时我发现其实w符合Q分布（对于100篇文章中，只有10篇才有这个单词），那么增加了这个额外的信息后，信息熵就增加了

---------即：单词w的出现代表了更多的信息。

因此，乘以IDF参数：log(D/j) 即为log p/log q，修正后的参数才是单词w的真正信息量。

最后对搜索者提供的所有单词组合，对候选的所有文章进行检索。按文章中针对提供的单词组合给出的信息量最大的网页进行排列。