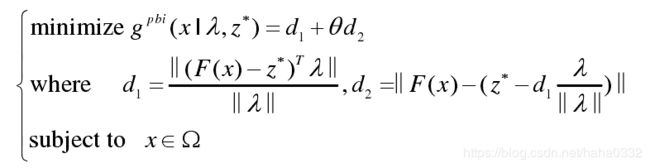MOP_3. 基于分解的多目标进化算法 —（MOEA/D)

多目标优化系列：

MOP_1. 多目标优化的相关基本概念

MOP_2. 非支配排序遗传算法 —（NSGA、NSGA-II)

MOP_3. 基于分解的多目标进化算法 —（MOEAD)

---

基于分解的多目标进化算法 (MOEA/D)

一种基于分解的多目标进化算法，是由张青富教授和李辉博士在 2007年发表在《IEEE Transactions on Evolutionary Computation》上的一篇文章。他们提出了区别于基于支配的MOEAs的另一种算法框架。

张青富教授专门为 MOEA/D 创建了相应的网站，网址为：http://dces.essex.ac.uk/staff/zhang/webofmoead.htm，上面有很多由 MOEA/D发展出来的新型且有效的 MOEAs，并且 MOEA/D 的原始模型以及各版本的代码都已经被共享，这样可以更大程度地吸引研究者们对MOEA/D发展的关注，同时对以后的研究者提供了便利学习的渠道。

基于分解的多目标进化算法（Multi-objective Evolutionary Algorithm Based on Decomposition, MOEA/D）将多目标优化问题被转化为一系列单目标优化子问题，然后利用一定数量相邻问题的信息，采用进化算法对这些子问题同时进行优化。因为Pareto前沿面上的一个解对应于每一个单目标优化子问题的最优解，最终可以求得一组Pareto最优解。由于分解操作的存在，该方法在保持解的分布性方面有着很大优势，而通过分析相邻问题的信息来优化，能避免陷入局部最优。

（1）MOEA/D 中使用的产生权向量的方法

MOEA/D 使用了单纯形格子点设计法来产生权向量。首先，需要确定一个正整数 H 。那么权向量的个数为 N ：，...... 由参数 H 控制。具体为每个权向量都会从集合中选取对应的值，所以权向量的个数可以通过公式  来计算。

举例：当m=3,H=1时，有3各权向量产生：(0,0,1),(0,1,0),(1,0,0);

           当m=3,H=2时，有6各权向量产生：(0,0,1),(0,1,0),(1,0,0),(0,1/2,1/2),(1/2,0,1/2),(1/2,1/2,0);

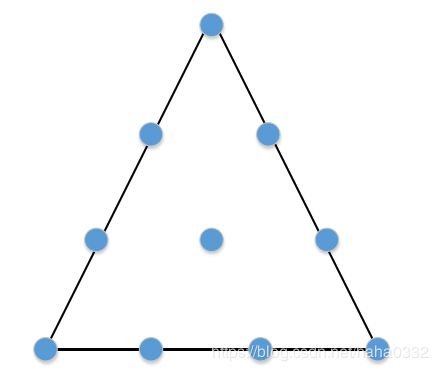
           当m=3,H=3时，有10各权向量产生：(0,0,1),(0,1,0),(1,0,0),(0,1/3,2/3),(0,2/3,1/3),(1/3,2/3,0),(2/3,1/3,0),(1/3,0,2/3),(2/3,0,1/3),(1/3,1/3,1/3);可以画出当 m=3，H =3时对应的点图：

可以看到在图中的 10 个点于三角平面内的分布实际上并不十分均匀，并且这些点中有太多的点都分布在了边界上，我们认为这将会使求得解的质量大受影响。 

（2）MOEA/D 中使用的分解方法

MOEA/D 使用的分解方法有：

加权和法（Weighted  sum  approach，简称 WS）；

切比雪夫法 (Weighted  Tchebycheff  approach ，简称 TCH) ；

基于惩罚的边界交集法（Penalty-based boundary intersection，简称 PBI）。

在（1）的权向量产生方法中可以预先产生一组权向量 ，其中，对于所有的 i=1,...,m，都有 ，且 。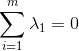

1）加权和法（WS）。经过这种方法分解后所得的单目标优化问题为：

（1-1）

其中 x 是需要优化的变量。加权和分解法将所有的目标函数做了累加处理，然后作为一个整体的子问题来进行求解。文献中表明这种分解方法对凸优化问题的效果较好，但是对于PF 为非凸的情况往往不能求得很好的解。

2）切比雪夫分解法（TCH）。经过这种方法分解后所得的单目标优化问题为：

（1-2）

其中，表示一系列参考点，也就是说，对于每一个 i=1,2,...,m，。可以知道对于一个Pareto最优解 ，必然会存在依据权向量  使得是（1-2）一个最优解，并且每一个（1-2）的最优解都会对应一个多目标优化问题的Pareto最优解，所以，通过改变权向量，我们就可以通过使用 TCH 分解法的 MOEA/D 来获得更多不同的 Pareto 最优解。

3）基于惩罚的边界交集法（PBI）。经过这种方法分解后所得的单目标优化问题为：

 

 （1-3）

其中，z的含义同2），表示一个惩罚因子，经验上，当解决目标个数大于 2 个的 MOPs 时，若使用相同分布的权向量，使用 PBI 分解法的 MOEA/D 会比使用 TCH 分解法的 MOEA/D 效果更加好。但是，这也需要为此付出代价，也就是必须设置有效的惩罚因子 。

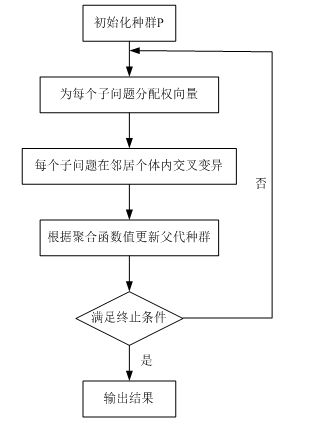
（3）算法框架

MOEA/D 的基本思想是使用一个聚合函数将一个 MOP 分解为一系列的单目标子优化问题，然后使用其他的进化算法对他们同时进行优化求解。

---

本文参考：

基于MOEA_D的改进研究_郑伟

基于分解的多目标进化算法（MOEA/D）