初学枚举——拨钟问题

                             初学枚举——拨钟问题（c++）

拨钟问题虽然可以采用暴力枚举求解，但寻找到该问题的局部，巧妙求解也是一个有趣的过程。

一、描述

有9个时钟，排成一个3*3的矩阵。现在需要用最少的移动，将9个时钟的指针都拨到12点的位置。共允许有9种不同的移动。如下表所示，每个移动会将若干个时钟的指针沿顺时针方向拨动90度。

移动    影响的时钟
1           ABDE
2           ABC
3           BCEF
4           ADG
5           BDEFH
6           CFI
7           DEGH
8           GHI
9           EFHI

输入
9个整数，表示各时钟指针的起始位置，相邻两个整数之间用单个空格隔开。其中，0=12点、1=3点、2=6点、3=9点。
输出
输出一个最短的移动序列，使得9个时钟的指针都指向12点。按照移动的序号从小到大输出结果。相邻两个整数之间用单个空格隔开。

二、分析

共9种移动方式，而每种移动方式最多进行3次，只需要在0到3间进行枚举。因为移动4次钟就会旋转360°回到原点，与密码锁问题里一个按钮按两次是一个原理。使用9重循环来暴力解决当然是能成功的，只需要在循环内部分别判断每个时钟的状态是否为0或者九个时钟的状态总和为0。

本文还是试图利用已有信息，寻找枚举的局部，简化问题。

如下图所示，我们把9种移动和时钟重合到一起，A——I对应1——9，此后移动和时钟都用数字1——9来表示。例如，从1指向2的箭头表示操作1号钟会对2号钟产生影响。而双箭头表示互相产生影响。别忘了，操作每个时钟也会对其本身产生影响。
              
操作1号钟或2号钟都会对其本身与另一个钟产生影响

                          
      操作5号钟会对其本身与2号钟产生影响


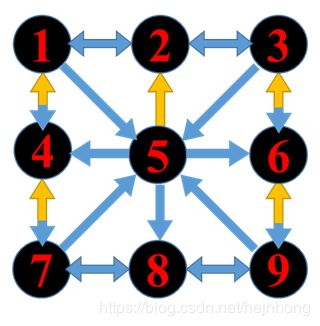
            整个时钟阵列的互相影响关系

这种相互影响还是比较复杂的，直接从上图是难以分析。按照熄灯问题的思路，我们尝试把第一层三个时钟（1, 2，3）当做局部来处理，如果只考虑下层时钟对上层时钟的影响。则影响关系图可简化如下：

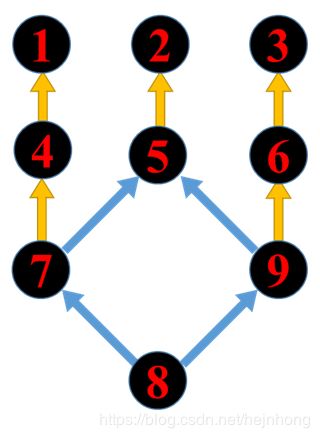
              下层时钟对上层时钟的影响

不难发现，1 , 2，3号时钟仅分别受到4，5，6号时钟的影响，所以当1，2，3号时钟作为局部被确定后，4，5，6号钟的操做次数也就确定了。同理7、9号钟的操作由4,、6号钟的状态确定。在7、9号钟操作后，5号钟的状态也确定了，其状态是最终的判断条件之一。

此外，第三层时钟的状态是不确定的。我们注意到图中的蓝色箭头，7号钟和9号钟的状态都将由8号钟的操作决定。8号钟的移动操作目标是使自身状态为0，当8号钟操作完后，如果7号和9号钟的状态都为0，那么就认为第三层拨钟都变为了0。综上5、7、9号钟的状态就是最终的判断条件。

基本思路如下

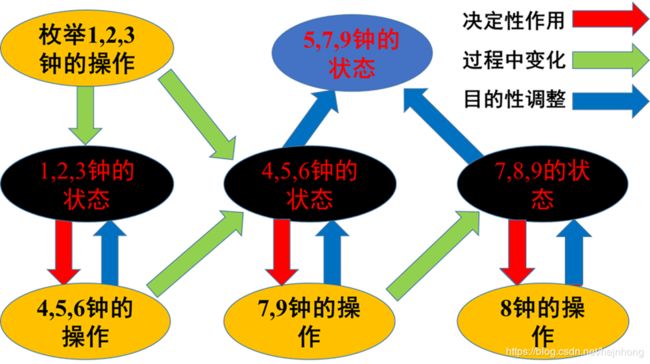
注意：图中7,9钟的操作是由4,6钟状态决定的，与5没有关系；7,9操作虽然调整了5号的状态，但这是一种过程中影响，并非目的；8号钟的操作仅由8号钟自身状态决定，目的是调整自身的状态，但其也决定了7、9号钟的最终状态。

三、源代码

#include
#include
using namespace std;
int main()
{
	int oriClock[10] = { 0 };//初始时钟状态
	int curClock[10] = { 0 };//当前时钟状态
	int move[10] = { 0 };    //移动操作次数

	for (int i = 1; i < 10; ++i//读入
		cin >> oriClock[i];

	for (move[1] = 0; move[1] < 4; ++move[1])
	{
		for (move[2] = 0; move[2] < 4; ++move[2])
		{
			for (move[3] = 0; move[3] < 4; ++move[3])
			{
				//枚举第一层的1，2，3号钟操作
				memcpy(curClock, oriClock, sizeof(oriClock));

				//1，2，3号钟操作对本层状态的影响
				curClock[1] = (curClock[1] + move[1] + move[2]) % 4;
				curClock[2] = (curClock[2] + move[1] + move[2] + move[3])%4;
				curClock[3] = (curClock[3] + move[2] + move[3]) % 4;
				
				//1，2，3号钟操作对下一层状态的影响
				curClock[4] = (curClock[4] + move[1]) % 4;
				curClock[5] = (curClock[5] + move[1] + move[3]) % 4;
				curClock[6] = (curClock[6] + move[3]) % 4;
				
				//1，2，3号钟状态决定下层的操作
				move[4] = (4 - curClock[1]) % 4;
				move[5] = (4 - curClock[2]) % 4;
				move[6] = (4 - curClock[3]) % 4;

				//4，5，6号钟操作对本层状态的影响
				curClock[4] = (curClock[4] + move[4] + move[5]) % 4;
				curClock[5] = (curClock[5] + move[5]) % 4;
				curClock[6] = (curClock[6] + move[5] + move[6]) % 4;
				
				//4，5，6号钟操作对下一层状态的影响
				curClock[7] = (curClock[7] + move[4]) % 4;
				curClock[8] = (curClock[8] + move[5]) % 4;
				curClock[9] = (curClock[9] + move[6]) % 4;
				
				//4，6号钟状态决定下层7，9的操作
				move[7]= (4 - curClock[4]) % 4;
				move[9] = (4 - curClock[6]) % 4;
				
				//7，9号钟操作对5号钟状态的影响
				curClock[5]= (curClock[5] + move[7] + move[9]) % 4;
				
				//7，9号钟操作对本层状态的影响
				curClock[7] = (curClock[7] + move[7]) % 4;
				curClock[8] = (curClock[8] + move[7] + move[9]) % 4;
				curClock[9] = (curClock[9] + move[9]) % 4;

				//8号钟状态决定8号钟的操作
				move[8] = (4 - curClock[8]) % 4;
				
				//8号钟操作对本层状态的影响
				curClock[7] = (curClock[7] + move[8]) % 4;
				curClock[9] = (curClock[9] + move[8]) % 4;

				if (curClock[5] + curClock[7] + curClock[9] == 0)//判断条件：5，7，9号钟
				{
					for (int i = 1; i < 10; ++i)
					{	
						while(move[i]--)
						cout << i << " ";
					}
					return 0;
				}

			}
		}
	}
	return 0;
}