多元统计分析——分类分析——基于Fisher线性判别分析（LDA）的分类
一、两分类问题
1、LDA分类
1.1、概念
判别分析旨在寻找一种分类规则，而分类分析更进一步：将新的观察对象分到一个合适的类别——即在分析过程中进行的预测。
Fisher判别分析的分类（LDA分类）是基于前面Fisher判别分析的思想进一步进行分类的。Fisher判别分析的思想是找到一个投影方向
，使得两个样本均值在上的投影，之间的标准化距离最大，如下图。
最后，我们求得的Fisher判别分析的判别函数![Z=a'y=[S_{pl}^{-1}(\overline{y}_{1}-\overline{y}_{2})]'y=(\overline{y}_{1}-\overline{y}_{2})'(S_{pl}^{-1})'y](http://img.e-com-net.com/image/info8/309d77be7d3a4f65a4fd972ebdc98740.gif){kind=small}
。由于
是协方差矩阵，则
。则
。
Fisher判别分析的原理可见《机器学习——数据降维——Fisher线性判别分析（LDA）》
如果现在我有一个新的观测点
，那么基于这个判别准则（投影），它到底是属于第一类还是第二类？
我们知道
在方向上的投影为：
，
在方向上的投影为：
，则
在方向上的投影为：
，从下图我们可以看出，
距离
较近，于是我们将分到
这一类。也就是说，当比和
的中点大，属于这一类。（注意：大小的比较和的方向有关，如果是由指向，则结论正好相反。）
归纳为数学通式为：
将
，
，
代入到上式得：
如果
，那么新观测对象分到类别，
如果
，那么新观测对象分到类别
。
以上就是整个基于判别分析的分类规则。
事实上，我们可以从数学角度验证：Fisher分类实际是在比较新观测对象与、之间的马氏距离：如果
，说明与更近，则应把分到；反之则应该分到。
1.2、错分率
真实数据中，任何分类规则通常都不能完全正确地分类。可以用如下表格表示总错分率（Total probability of misclassification,TPM）
其中总错分率等于，样本被分为实际上来自的概率，加上样本被分为实际上来自的概率：
。
更多有监督分类算法的模型评估指标详见《机器学习——有监督分类——混淆矩阵（Confusion Matrix）》
1.3、案例
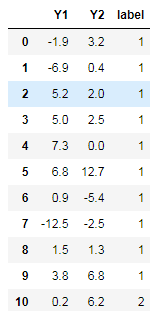
“今天”和“昨天”的湿度差（
）和温度差（
）是用来预测“明天”是否会下雨的两个很重要的因素，数据如下；其中label=1表示雨天，label=2表示阴天。
1.3.1、绘制散点图：
plt.scatter(data['Y1'],data['Y2'],c=data['label'])输出：
1.3.2、用Fisher‘s LDA分类，并建立Fisher判别函数：
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
X=data.iloc[:,:-1] #特征
Y=data.iloc[:,-1] #标签
model_lda= LDA(
#n_components=1 #如果我们只是为了降维，则只需要输入n_components，注意这个值必须小于"类别数-1"
)
data_tranform=model_lda.fit_transform(X,Y) #训练模型
model_lda.coef_ #判别系数（投影向量）
输出：
array([[-0.17102835, 0.37135367]])
Fisher判别函数为：
，注意：此处的和并不是原有样本数据，而是经过相应处理后（标准化、去中心化）的数据。
1.3.3、利用模型回测现有样本：
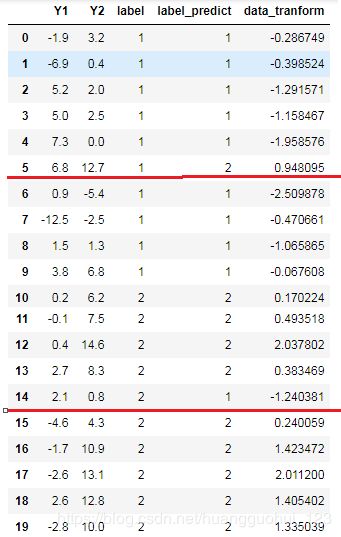
Y_predict=model_lda.predict(X) #利用训练的模型回测现有样本
data['label_predict']=Y_predict #保存预测分类结果
data['data_tranform']=data_tranform #降维之后的数据（一维）
data输出
其中label_predict是模型预测的分类，我们发现，第5样本和第14样本是预测错误的，data_tranform是降维（投影）之后的数据，也就是
对应的值。
1.3.4、计算总错分率（TPM）：
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict) #1-准确率输出：
0.1错分率为0.1，在合理的范围之内，可以得出整体的分类效果是不错的。
我们也可以以箱线图的形式，来看转换（降维）之后的数据是否被很好的分开：
plt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig=plt.figure(figsize=(6,3)) #表示绘制图形的画板尺寸为6*4.5；
ax=fig.add_subplot(1,2,1)
plt.boxplot([data[data['label']==1]['data_tranform'],data[data['label']==2]['data_tranform']])
plt.title('原标签')
ax=fig.add_subplot(1,2,2)
plt.boxplot([data[data['label_predict']==1]['data_tranform'],data[data['label_predict']==2]['data_tranform']])
plt.title('分类标签')
plt.show()输出：
我们看第一张图，虽然有部分极端值使得箱线图有所重合，但是大部分数据（箱体）是被很好的分开着的，Fisher‘s LDA分类效果很好。
1.3.5、预测未来数据
如果我们得知今天的数据是
，如何预测明天的天气？
model_lda.predict(pd.DataFrame([[8.0,2.0]]))输出：
array([1], dtype=int64)
即根据Fisher‘s LDA分类法则，预测明天为雨天。
二、多分类问题
类似于两总体情形，假设协方差矩阵相同，Fisher分类法则等价于比较新观测对象和各样本均值
之间的马氏距离：
，并将其分到有最小距离的群体。
也就是说我们如果用Fisher分类法则的话，我们只需要比较到底新的观测值跟哪个群体的马氏距离最近，我们就把它分到这个群体。
案例：研究团队调查了20个品牌的电视机，记录了它们的市场定位（G）：1.高端市场，2. 中端市场，3. 低端市场；质量评估得分（Q），功能评估得分（C）和价格（P，单位为每百元人民币）。如果一个全新的品牌被推出，其中
,它的市场定位应如何？
2.1、导入数据
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data=pd.read_excel('D:/CDA/dataset/data_LDA&bayers_2.xlsx')
data输出：
2.2、两两散点图
sns.pairplot(data,hue="G")输出：
从图中可以看出，以其中的两个指标来划分群体，分类都不是特别明显。
2.3、Fisher's LDA分类，并利用训练好的模型回测数据
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
X=data.iloc[:,:-1] #特征
Y=data.iloc[:,-1] #标签
model_lda= LDA(
# n_components=1 #如果我们只是为了降维，则只需要输入n_components，注意这个值必须小于"类别数-1"
)
data_tranform=model_lda.fit_transform(X,Y) #训练模型
Y_predict=model_lda.predict(X) #利用训练的模型回测数据
data['label_predict']=Y_predict #保存预测分类结果
data_=pd.concat([data,pd.DataFrame(data_tranform,columns=['LD1','LD2'])],axis=1) #保存降维之后的结果（2维）
data_
输出：
2.4、计算总错分率（TPM）：
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict) #1-准确率输出：
0.1错分率为0.1，在合理的范围之内，可以得出整体的分类效果是不错的。
2.5、预测未来数据
model_lda.predict(pd.DataFrame([[8.0,7.5,65]]))输出：
array([2], dtype=int64)即根据Fisher‘s LDA分类法则，预测为中端市场。
三、局限性
由于我们没有对分布作假设，因此 Fisher 法则是一种非参数方法，但是当样本是正态分布或者有线性趋势，LDA能表现的更好。如下非线性分类问题中，Fisher判别分析就失效了。
应对这样的数据集，我们可能得用机器学习的方法，或者非线性的方法进行分类。
