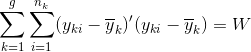多元统计分析——数据降维——Fisher线性判别分析(LDA)
一、LDA的思想
Fisher线性判别分析(Fisher's Linear Discriminant Analysis, 以下简称LDA)是一种有监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。通俗理解就是:将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大,如下图所示。
只所以称为线性判别分析,其实是因为其最早用在分类当中:判别分析是寻找一种“分类规则”,即利用变量的函数(判别函数)来描述(解释)两组或多组之间的区别。
例如对于银行来说,最重要的是判断申请者是否能够成功还款,以此作为是否给其贷款的依据。判别分析即利用历史数据(成功还款和未偿还贷款),通过两类人的一些有区别的特征(年龄、收入等),找到一个“最优”的规则区分这两类人。
二、二类LDA原理
1、原理
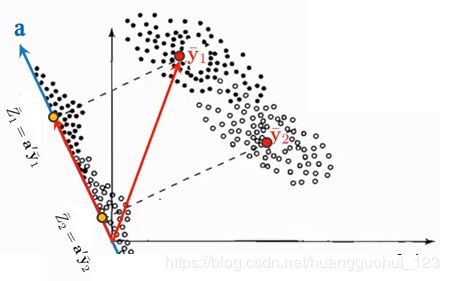
上面我们已经知道,Fisher线性判别分析的思想是寻找两个群体“最好”的线性判别法则,来最大限度的区分两个群体。从几何角度上理解,其实也就是找到一个最佳的投影线(定义为![]() ),使其在该投影线上的投影最大限度的分开,对于该投影线,我们只要找到其方向就可以了。如下图所示:
),使其在该投影线上的投影最大限度的分开,对于该投影线,我们只要找到其方向就可以了。如下图所示:
我们假设有两个群体,总体均值向量![]() ,但具有相同的协防差矩阵
,但具有相同的协防差矩阵![]() 。
。
从中抽取两个随机样本:
第一个![]() 维样本
维样本![]() 的样本均值向量为
的样本均值向量为![]() ,则样本的协方差矩阵为
,则样本的协方差矩阵为![]() 。
。
第二个![]() 维样本
维样本![]() 的样本均值向量为
的样本均值向量为![]() ,则样本的协方差矩阵为
,则样本的协方差矩阵为![]() 。
。
类似于两样本的![]() 检验,我们比较两个群体,只要比较两个群体的均值即可。这里也是,我们只要使得原始均值向量
检验,我们比较两个群体,只要比较两个群体的均值即可。这里也是,我们只要使得原始均值向量![]() 在
在![]() 上的投影距离最大(下图黄线的长度)即可。
上的投影距离最大(下图黄线的长度)即可。
由线性代数我们知道:如果![]() 为单位向量,
为单位向量,![]() 即为
即为![]() 在
在![]() 方向上的投影向量长度。则
方向上的投影向量长度。则![]() 在
在![]() 方向上的投影向量长度我们可以表示为:
方向上的投影向量长度我们可以表示为:![]() ,
,![]() 在
在![]() 方向上的投影向量长度表示为:
方向上的投影向量长度表示为:![]() ,两投影的距离为
,两投影的距离为![]() ,即我们的目的:找到一个
,即我们的目的:找到一个![]() ,使得
,使得![]() 最大。
最大。
上面 ![]() ,我们衡量的是欧式距离,我们知道欧式距离的缺陷在于:1、欧式距离易受变量不同量纲的影响;2、没有考虑变量之间的相关性。
,我们衡量的是欧式距离,我们知道欧式距离的缺陷在于:1、欧式距离易受变量不同量纲的影响;2、没有考虑变量之间的相关性。
关于欧式距离和马氏距离的区别可参考:《多元统计分析——欧式距离和马氏距离》
我们知道:马氏距离即是我们将向量“标准化”过后的欧式距离,如何标准化,即乘上向量其自身的协防差矩阵的逆的矩阵根。
![]() 的协方差矩阵
的协方差矩阵![]() 。
。
其中![]() ,由上面的假设我们已知两总体是具有相同的协方差矩阵
,由上面的假设我们已知两总体是具有相同的协方差矩阵![]() ,借助
,借助![]() 检验中的“两均值之差的方差等于两均值方差的之和”的思想,我们知道多元统计分析同样具有这样的性质:
检验中的“两均值之差的方差等于两均值方差的之和”的思想,我们知道多元统计分析同样具有这样的性质:![]() 。
。
总体的协方差矩阵![]() 我们一般是未知的,我们一般以样本的协方差矩阵
我们一般是未知的,我们一般以样本的协方差矩阵![]() 代替,得
代替,得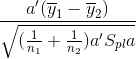
为了避免负数的出现,我们对马氏距离加上一个平方,则投影后马氏距离的平方,我们定义成![]() :
:
Fisher线性判别分析的思想即为找到一个![]() 使得
使得![]() 最大,由于
最大,由于![]() 对
对![]() 求极值无影响,可去掉。
求极值无影响,可去掉。
2、利用柯西不等式求最大值
由上面我们已知:寻找两个群体“最好”的线性判别法则问题转换为求![]() 极值得问题。
极值得问题。
我们知道柯西不等式的一般表示式为:![]() ,当
,当![]() 时取等。
时取等。
我们令![]() ,
,![]() ,则不等式左边变成:
,则不等式左边变成:![]() ,不等式右边变成
,不等式右边变成,组成变形后的柯西不等式为:
![]() ,当
,当![]() 时取等。
时取等。
关于柯西不等式可参考:《线性代数——柯西不等式》
参考柯西不等式:![]() ,
,![]() 时取等,我们可以求
时取等,我们可以求![]() 的极值条件,即为
的极值条件,即为![]() 时,
时,![]() 取最大值。
取最大值。
其中,![]() 被称为判别函数系数,
被称为判别函数系数,![]() 被称为Fisher判别函数。
被称为Fisher判别函数。
3、案例
有两个样本数据,有两个维度进行刻画,已知第一个样本![]() ,第二个样本
,第二个样本![]() ,协方差矩阵
,协方差矩阵![]() ,样本数据分布如下:
,样本数据分布如下:
如果这些点投影到![]() 轴或者
轴或者![]() 轴,会有较大的重叠,在单个维度上,我们可以用
轴,会有较大的重叠,在单个维度上,我们可以用![]() 检验进行检验:
检验进行检验:
双侧检验![]() (显著性水平
(显著性水平![]() ),即两样本在单个维度上的差别不显著。
),即两样本在单个维度上的差别不显著。
但是,我们还是可以很好的将其分开,如下图:
其中![]() 和
和![]() 分别代表了样本两个维度的数据,我们将原始数据代入到判别函数
分别代表了样本两个维度的数据,我们将原始数据代入到判别函数![]() ,算出来的
,算出来的![]() 即为降维过后的数据(点在
即为降维过后的数据(点在![]() 上的投影坐标),即实现了原来二维的数据降到一维。
上的投影坐标),即实现了原来二维的数据降到一维。
注意:![]() 中,系数代表每个变量对区分规则的贡献,如果变量的量级差别较大,我们可以先进行标准化处理再进行判别分析。
中,系数代表每个变量对区分规则的贡献,如果变量的量级差别较大,我们可以先进行标准化处理再进行判别分析。
三、多类LDA原理
1、原理
现有![]() 个群体
个群体![]() ,
,![]() ,第
,第![]() 个群体样本为
个群体样本为![]() ,其中
,其中![]() 代表第第
代表第第![]() 个群体的样本容量,第
个群体的样本容量,第![]() 个群体的样本均值为
个群体的样本均值为![]() ,所有群体的样本均值为
,所有群体的样本均值为 。
。
借助简单统计学中的方差分析的思想:
如果各个群体均数相等,![]() 的数值不会太大(在1的左右不会太远)。相反,如果的数值过大,“各个群体均数相等”这个假设就值得怀疑了。
的数值不会太大(在1的左右不会太远)。相反,如果的数值过大,“各个群体均数相等”这个假设就值得怀疑了。
关于方差分析可参考:《统计推断——假设检验——方差分析》
而LDA的思想可以用一句话概括,就是“经过![]() 投影后组内方差最小,组间方差最大”,当然这个
投影后组内方差最小,组间方差最大”,当然这个![]() 就可能有多个了。
就可能有多个了。
组间平方和为:
![]() ,
,![]() 代表原始样本数据的组间方差矩阵。
代表原始样本数据的组间方差矩阵。
组内平方和为:
![]() ,
,![]() 代表原始样本数据的组内方差矩阵。
代表原始样本数据的组内方差矩阵。
![]() 这一表达在数学物理中被称为广义瑞利熵,关于广义瑞利熵的概念和应用大家可以自己查阅相关资料。我们这边直接应用性质进行
这一表达在数学物理中被称为广义瑞利熵,关于广义瑞利熵的概念和应用大家可以自己查阅相关资料。我们这边直接应用性质进行![]() 最大化的求解。
最大化的求解。
最大化瑞利熵的必要条件是:存在一个向量![]() 使得
使得![]() ,稍微变形一下:
,稍微变形一下:![]() ,这个正好就是我们对特征值和特征向量的定义一致,即
,这个正好就是我们对特征值和特征向量的定义一致,即![]() 是方阵
是方阵![]() 的特征值,
的特征值,![]() 为方阵
为方阵![]() 以
以![]() 为特征值对应的特征向量。即求
为特征值对应的特征向量。即求![]() 数值得最大化问题转换为求
数值得最大化问题转换为求![]() 的特征根问题。
的特征根问题。
2、LDA算法流程
以下是LDA算法的大致流程:
- 计算组间方差矩阵
 ;
; - 计算组内方差矩阵

 ;
; - 计算矩阵
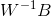 ;
; - 计算
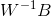 的特征值
的特征值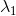 ,
, ,....,
,....,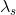 以及对应的特征向量
以及对应的特征向量 ,
,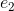 ,...,
,...,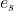 。
。 - 将特征值
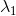 ,
, ,....,
,....,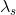 按照从大到小的顺序排列,选择非零特征值及对应的特征向量(
按照从大到小的顺序排列,选择非零特征值及对应的特征向量(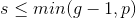 ,
,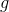 代表组数,
代表组数, 代表样本数据维度,如原始数据是3个组群,5个维度的数据,则非零特征值最多为2个),注意:非零特征值的意思是抛弃无限接近0的特征值,可通过特征值的占比来筛选特征值。
代表样本数据维度,如原始数据是3个组群,5个维度的数据,则非零特征值最多为2个),注意:非零特征值的意思是抛弃无限接近0的特征值,可通过特征值的占比来筛选特征值。 - 将样本
 投影到新的空间
投影到新的空间 ,即得到了LDA降维后的结果。
,即得到了LDA降维后的结果。 - ***计算Fisher判别函数:
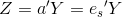 ,其中
,其中 根据数据维度可分解为
根据数据维度可分解为![\left [ y_{1},y_{2},...,y_{p} \right ]](http://img.e-com-net.com/image/info8/b8cc83d453af43f7beca0356e1506047.gif) ,注意:输出的判别函数即为分类的规则,有多少个特征向量
,注意:输出的判别函数即为分类的规则,有多少个特征向量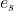 ,就有多少个判别式****。
,就有多少个判别式****。
注意:1、上面第四步所说的非零特征值其实是特征值无限接近0的特征值,即特征值占总特征值之和的占比很小。
2、第七步中计算Fisher判别函数,是多元统计分析用于刻画分类规则而产生的,如果单纯为了实现降维,可跳过这一步。
3、案例
科考人员从加利福尼亚的砂岩中收集了原油样本。这些原油分别来自三类地层(3个类别)中的一类:
现试图基于砂岩中五种化学成分含量(5个维度),找到一种划分地层类别的方法
数据样本如下:
使用pairplot()函数可以画全局图,即两两变量之间的分布关系。
对角线的分布图,单从各个维度上看,各组的数据都有较大的重叠,即从单一维度上,无法较好的区分数据。
使用LDA算法降维过程:
#租的标签
clusters=np.unique(data['label'])
#组间协方差矩阵
B = np.zeros((data.shape[1]-1,data.shape[1]-1)) #构造一个和原始数据特征维度一样的方阵B
y_hat = data.iloc[:,:-1].mean(0) #所有样本的平均值
for i in clusters:
Ni = data[data['label'] == i].iloc[:,:-1].shape[0] #各个样本的样本数
ui = data[data['label'] == i].iloc[:,:-1].mean(0) #某个类别的平均值
SBi = Ni*np.dot(np.mat(ui - y_hat).T,np.mat(ui - y_hat))
B += SBi
B输出:
array([[ 7.82102934e+01, -4.51200260e+02, 7.66358682e+00,
-4.46707730e+01, -7.10295522e+01],
[-4.51200260e+02, 2.65873662e+03, -4.31571861e+01,
2.50295766e+02, 4.89521636e+02],
[ 7.66358682e+00, -4.31571861e+01, 7.70884752e-01,
-4.51741260e+00, -5.45103771e+00],
[-4.46707730e+01, 2.50295766e+02, -4.51741260e+00,
2.65002117e+01, 2.99625104e+01],
[-7.10295522e+01, 4.89521636e+02, -5.45103771e+00,
2.99625104e+01, 1.78617620e+02]])#组内协方差矩阵
W = np.zeros((data.shape[1]-1,data.shape[1]-1)) #构造一个和原始数据特征维度一样的方阵W
for i in clusters:
data_i=data[data['label'] == i]
data_i=data_i.iloc[:,:-1]
y_i_hat=data_i.mean(0) #组内平均值
for i in range(data_i.shape[0]):
data_i_k = data_i.iloc[i,:]
Swi = np.dot(np.mat(data_i_k-y_i_hat).T,np.mat(data_i_k-y_i_hat))
W += Swi
W输出:
array([[ 9.19015584e+01, 1.02800260e+02, -2.87254978e+00,
1.48740260e+00, 3.66821818e+01],
[ 1.02800260e+02, 1.73134338e+03, 9.67186147e-01,
6.24842338e+01, 8.55836364e+00],
[-2.87254978e+00, 9.67186147e-01, 1.43065599e+00,
2.92030519e+00, -1.33146970e+00],
[ 1.48740260e+00, 6.24842338e+01, 2.92030519e+00,
2.45342623e+01, 1.56760636e+01],
[ 3.66821818e+01, 8.55836364e+00, -1.33146970e+00,
1.56760636e+01, 1.71479255e+02]])step3:计算矩阵![]() 。
。
S = np.dot(np.linalg.inv(W),B)
S输出:
array([[ 1.82516012e+00, -1.07591870e+01, 1.74495236e-01,
-1.01190860e+00, -1.98628881e+00],
[-2.80144016e-01, 1.70631002e+00, -2.57448644e-02,
1.48018421e-01, 3.83404462e-01],
[ 1.41480726e+01, -7.79818659e+01, 1.45518636e+00,
-8.56489218e+00, -7.64169791e+00],
[-2.62000045e+00, 1.37399432e+01, -2.82742831e-01,
1.67932992e+00, 4.11969952e-01],
[-4.41300084e-01, 3.20954366e+00, -3.06844034e-02,
1.63783970e-01, 1.35039633e+00]])step4:计算![]() 的特征值
的特征值![]() ,
,![]() ,....,
,....,![]() 以及对应的特征向量
以及对应的特征向量![]() ,
,![]() ,...,
,...,![]() 。
。
eigVals,eigVects = np.linalg.eig(S) #求特征值,特征向量
eigpairs = [(np.abs(eigVals[i]), eigVects[:,i]) for i in range(len(eigVals))] #将特征值和对应的特征向量绑定成一个元祖。
eigpairs输出:
[(6.736305722392899,
array([ 0.12841268+0.j, -0.01991815+0.j, 0.97486544+0.j, -0.17787167+0.j,
-0.03335415+0.j])),
(6.245004513516506e-17,
array([-0.30577419+0.j, -0.01618153+0.j, 0.9340433 +0.j, -0.18296885+0.j,
-0.01805021+0.j])),
(1.2800770307908278,
array([ 0.03545112+0.j, -0.01766616+0.j, -0.93249504+0.j, 0.32884656+0.j,
-0.14402803+0.j])),
(3.782695793427638e-16,
array([ 0.20869023-0.05456166j, 0.02924344-0.02887822j,
0.93259111+0.j , 0.24577484+0.14294114j,
-0.0099238 +0.03346897j])),
(3.782695793427638e-16,
array([ 0.20869023+0.05456166j, 0.02924344+0.02887822j,
0.93259111-0.j , 0.24577484-0.14294114j,
-0.0099238 -0.03346897j]))]step5:将特征值![]() ,
,![]() ,....,
,....,![]() 按照从大到小的顺序排列,选择非零特征值及对应的特征向量(
按照从大到小的顺序排列,选择非零特征值及对应的特征向量(![]() ,
,![]() 代表组数,
代表组数,![]() 代表样本数据维度,如原始数据是3个组群,5个维度的数据,则非零特征值最多为2个),注意:非零特征值的意思是抛弃无限接近0的特征值,可通过特征值的占比来筛选特征值。
代表样本数据维度,如原始数据是3个组群,5个维度的数据,则非零特征值最多为2个),注意:非零特征值的意思是抛弃无限接近0的特征值,可通过特征值的占比来筛选特征值。
eigpairs = sorted(eigpairs, key=lambda k: k[0], reverse=True) # 根据特征值降序排序
eigpairs输出:
[(6.736305722392899,
array([ 0.12841268+0.j, -0.01991815+0.j, 0.97486544+0.j, -0.17787167+0.j,
-0.03335415+0.j])),
(1.2800770307908278,
array([ 0.03545112+0.j, -0.01766616+0.j, -0.93249504+0.j, 0.32884656+0.j,
-0.14402803+0.j])),
(3.782695793427638e-16,
array([ 0.20869023-0.05456166j, 0.02924344-0.02887822j,
0.93259111+0.j , 0.24577484+0.14294114j,
-0.0099238 +0.03346897j])),
(3.782695793427638e-16,
array([ 0.20869023+0.05456166j, 0.02924344+0.02887822j,
0.93259111-0.j , 0.24577484-0.14294114j,
-0.0099238 -0.03346897j])),
(6.245004513516506e-17,
array([-0.30577419+0.j, -0.01618153+0.j, 0.9340433 +0.j, -0.18296885+0.j,
-0.01805021+0.j]))]计算特征值占比:
# 通过特征值的比例来筛选特征值
for i,j in enumerate(eigpairs):
print('eigVal%s: %f' %(i+1, (j[0]/eigVals.sum())))输出:
eigVal1: 0.840317
eigVal2: 0.159683
eigVal3: 0.000000
eigVal4: 0.000000
eigVal5: 0.000000筛选特征向量组成映射矩阵:
#选择非零特征值对应的特征向量作为映射矩阵Z
Z= np.vstack((eigpairs[0][1], eigpairs[1][1])).T
Z输出:
array([[ 0.12841268+0.j, 0.03545112+0.j],
[-0.01991815+0.j, -0.01766616+0.j],
[ 0.97486544+0.j, -0.93249504+0.j],
[-0.17787167+0.j, 0.32884656+0.j],
[-0.03335415+0.j, -0.14402803+0.j]])step6:将样本![]() 投影到新的空间
投影到新的空间![]() ,即得到了LDA降维后的结果,降维后为2维特征。
,即得到了LDA降维后的结果,降维后为2维特征。
data_=np.dot(np.mat(data.iloc[:,:-1]),Z)
data_输出:
matrix([[-1.98240436+0.j, -0.38325885+0.j],
[-2.23895967+0.j, -0.24869691+0.j],
[-1.68704195+0.j, -0.142058 +0.j],
[-2.13486186+0.j, -0.26578783+0.j],
[-2.17974478+0.j, -0.03259639+0.j],
[-1.74667874+0.j, -0.13214131+0.j],
[-1.55953271+0.j, -0.13844398+0.j],
[-1.68508356+0.j, 0.72475706+0.j],
[-1.1974488 +0.j, 0.60711313+0.j],
[-1.17539724+0.j, 1.19866906+0.j],
[-0.46583313+0.j, 1.35188424+0.j],
[-1.50070354+0.j, 1.37555728+0.j],
[-0.75650544+0.j, 0.6157262 +0.j],
[-1.31782703+0.j, 0.74866093+0.j],
[-1.32474307+0.j, 1.14561945+0.j],
[-1.26497509+0.j, 0.19023476+0.j],
[-1.816251 +0.j, 0.92796843+0.j],
[-1.48223369+0.j, -0.29111897+0.j],
[ 0.00748193+0.j, -0.26936795+0.j],
[-0.08522769+0.j, 0.23168825+0.j],
[-0.41231509+0.j, 0.83135552+0.j],
[ 0.23014115+0.j, -0.0957719 +0.j],
[ 0.02054684+0.j, 0.06162732+0.j],
[ 0.48231118+0.j, 0.17544311+0.j],
[ 0.11349465+0.j, 0.32497595+0.j],
[-0.11256643+0.j, 0.03207345+0.j],
[ 0.46192225+0.j, -0.2352691 +0.j]])降维后的数据可视化:
data_=pd.DataFrame(data_)
data_['label']=data['label']
plt.scatter(data_[0],data_[1],c=data['label'],cmap='rainbow')输出:
step7:计算Fisher判别函数:![]() ,其中
,其中![]() 根据数据维度可分解为
根据数据维度可分解为![]() ,注意:输出的判别函数即为分类的规则,有多少个特征向量
,注意:输出的判别函数即为分类的规则,有多少个特征向量![]() ,就有多少个判别式。
,就有多少个判别式。
本案例的降维之后的2维数据,第一维度可用判别式![]() 表示,第二维度可用判别式
表示,第二维度可用判别式![]() 表示。
表示。
五、LDA与PCA的联系和区别
LDA用于降维,和PCA有很多相同,也有很多不同的地方,因此值得好好的比较一下两者的降维异同点。
1、相同点:
- 两者均可以对数据进行降维。
- 两者在降维时均使用了矩阵特征分解的思想。
- 两者都假设数据符合高斯分布。
2、不同点:
- LDA是有监督的降维方法,而PCA是无监督的降维方法(可以理解为LDA寻求的是两个或多个群体之间距离最大化的线性组合,而PCA中只有一个群体,目标是找到能使这个群体中个体之间分得最开的变量组合)。
- LDA降维最多降到类别数
 的维数,所以当数据维度很高,但是类别数少的时候,算法并不适用。而PCA没有这个限制。
的维数,所以当数据维度很高,但是类别数少的时候,算法并不适用。而PCA没有这个限制。 - LDA除了可以用于降维,还可以用于分类。
- LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
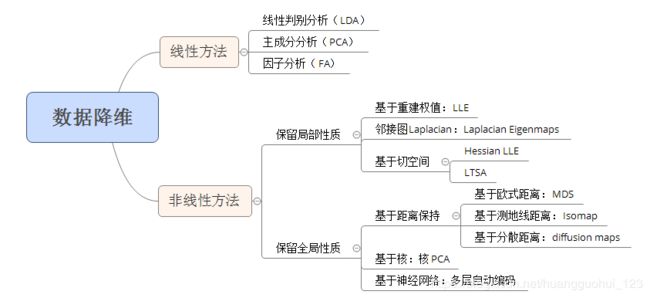
这点可以从下图形象的看出,在某些数据分布下LDA比PCA降维较优。
我们知道:LCA是选组间变异最大的投影方向(可理解为每组均值的变异),而PCA选择样本点投影具有最大方差的方向。如上图左图,均值相隔较远,则LCA降维之后的效果优于PCA;右图,均值相隔很近,则LDA降维之后的效果不如PCA。
3、LDA算法主要优点:
- 在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识。
- LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优。
4、LDA算法主要缺点:
- LDA不适合对非高斯分布样本进行降维,PCA也有这个问题。
- LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。目前有一些LDA的进化版算法可以绕过这个问题。
- LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好。
- LDA可能过度拟合数据。



![t^{2}(a)=\frac{[{a}'(\overline{y}_{1}-\overline{y}_{2})]^{2}}{(\frac{1 }{n_{1}}+\frac{1}{n_{2}})a'S_{pl} a}\propto \frac{[{a}'(\overline{y}_{1}-\overline{y}_{2})]^{2}}{a'S_{pl} a}](http://img.e-com-net.com/image/info8/2a7db3b3e98b481589ed4fd06e12619a.gif)



![SSG=\sum ^{g}_{k=1}n_{k}(a'\overline{y}_{k}-a'\overline{y})^{2}=a'[\sum ^{g}_{k=1}n_{k}(\overline{y}_{k}-\overline{y})'(\overline{y}_{k}-\overline{y})]a](http://img.e-com-net.com/image/info8/b3e2545cff6f4ec68ec907c25a7da3a6.gif)

![SSE=\sum ^{g}_{k=1}\sum ^{n_{k}}_{i=1}(a'y_{ki}-a'\overline{y}_{k})^{2}=a'[\sum ^{g}_{k=1}\sum ^{n_{k}}_{i=1}(y_{ki}-\overline{y}_{k})'(y_{ki}-\overline{y}_{k})]a](http://img.e-com-net.com/image/info8/7381ced5c3484a7493763b43567fbc9b.gif)