多元统计分析——分类分析——贝叶斯分类
一、两分类问题
1、贝叶斯分类
1.1、分类规则
![]() 和
和![]() 代表两个总体,各自的先验概率为
代表两个总体,各自的先验概率为![]() 和
和![]() (
(![]() ),
),![]() 和
和![]() 分别是总体
分别是总体![]() 和
和![]() 中
中![]() 的概率密度函数。
的概率密度函数。
![]() 和
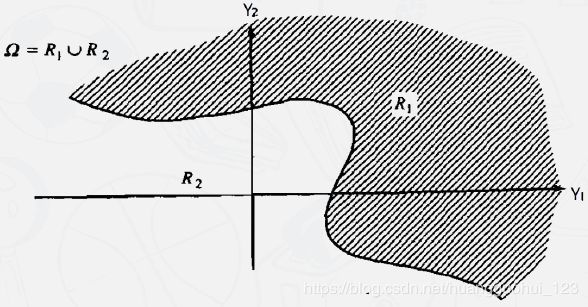
和![]() 代表按分类规则划分的两组区域。例如,如果一个新观测对象分到
代表按分类规则划分的两组区域。例如,如果一个新观测对象分到![]() ,那么我们声明该样本来自总体
,那么我们声明该样本来自总体![]() ,
,![]() 。
。 ![]() 和
和![]() 是整个空间的分割。
是整个空间的分割。
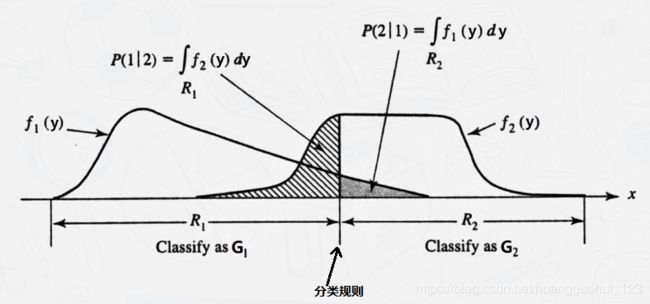
![]() 是“我们将样本
是“我们将样本![]() 分为
分为![]() 然而实际上它来自
然而实际上它来自![]() ”的条件概率:
”的条件概率:![]() ,类似的,
,类似的,![]() ,具体分布如下图所示。
,具体分布如下图所示。
进而我们可以推导总错分率 (TPM):
![]() (观测对象被错分到
(观测对象被错分到![]() )=
)=![]()
![]() (观测对象被错分到
(观测对象被错分到![]() )=
)=![]()
记![]() 是错误地将来自总体
是错误地将来自总体![]() 的观测对象
的观测对象![]() 错分到
错分到![]() 的代价/成本,类似可定义
的代价/成本,类似可定义![]() 是错误地将来自总体
是错误地将来自总体![]() 的观测对象
的观测对象![]() 错分到
错分到![]() 的代价/成本,如下图。
的代价/成本,如下图。
我们知道,LDA是没有考虑代价的,它考虑的是一个概率,我们想让样本之间分的越开越好(错分率越少越好)。贝叶斯是可以考虑代价的, 于是贝叶斯考虑的是期望代价(Expected cost of misclassification, ECM),贝叶斯分类的目标是最小化错分的期望代价ECM:
![]()
如何最小化![]() ?
?
贝叶斯分类的目标是找到一个分类法则,使得最小化![]() ,这个分类法则与
,这个分类法则与![]() 和
和![]() 区域的划分有关,上式当中
区域的划分有关,上式当中![]() 这项和
这项和![]() 的取值是没有关系的,进而:
的取值是没有关系的,进而:
分类规则问题转化为:找到一个区域![]() ,使得
,使得![]() 在
在![]() 的积分最小。
的积分最小。
我们知道积分是曲线下的有向面积,如果![]() ,则越积越多,如果
,则越积越多,如果![]() ,则越积越少。换句话说,要使得
,则越积越少。换句话说,要使得![]() 在
在![]() 的积分最小,
的积分最小,![]() 应取值所有使得
应取值所有使得![]() 的
的![]() 值。
值。
定理(贝叶斯分类法则):
![]() :
:![]()
![]() :
:![]()
化简得:
特殊情形
1.2、与LDA的区别
| LDA分类 | 贝叶斯分类 | |
| 是否考虑先验概率 | 否 | 是 |
| 是否考虑误判代价 | 否 | 是 |
| 是否事先假设总体分布 | 不需要分布假设 | 需要明确 |
| 是否事先假设总体协方差矩阵 | 需要同协方差矩阵假设 | 不需要协方差矩阵假设 |
| 是否线性 | 是 | 否 |
| 分类目标 | 最小化错分率 | 最小化错分的期望代价 |
在前面我们讲到《多元统计分析——分类分析——基于Fisher线性判别分析(LDA)的分类》当中,LDA分类完全是基于样本数据来呈现的(找一个投影方向,让两组数据分的最开),没有考虑到任何先验的信息。贝叶斯的优势正好在于考虑了先验的信息。有关先验概率的相关知识可见《统计推断——独立事件、条件概率、贝叶斯定理(先验分布/后验分布/似然估计)》。
例如:通常,一家公司陷入财务困境并最终破产的(先验)概率很小,所以我们应该首先默认一家随机选择的公司不会破产,除非数据压倒性地支持公司将会破产这一事件。所以这时事件发生的先验概率(Prior probability)应该被考虑在内。
另外,我们在LDA分类当中,只考虑了误判的概率,并没有考虑产生误判之后的代价(成本),但是在实际生活当中,从第一类错分到第二类与第二类错分到第一类的代价往往是不一样的。
例如:没有诊断出绝症的“代价”明显大于将病人误诊为绝症,所以这时“误判代价 ”(Misclassification cost)应该被考虑在内。
所以,贝叶斯分类之于Fisher's LDA分类,它的优势在于考虑了这两点:先验概率(Prior probability),误判代价 (Misclassification cost)。
1.3、与LDA的联系
当两群体来自具有相同协方差矩阵的正态分布![]() 和
和![]() 时,贝叶斯法则则可以表示为:
时,贝叶斯法则则可以表示为:
![]() :
:
回想LDA分类法则为![]() :
:![]() ,即我们可以得出结论:当两群体来自具有相同协方差矩阵的正态分布时,贝叶斯法则的特殊情形——当
,即我们可以得出结论:当两群体来自具有相同协方差矩阵的正态分布时,贝叶斯法则的特殊情形——当![]() (先验概率相同且错分成本相同),等价于LDA分类法则。
(先验概率相同且错分成本相同),等价于LDA分类法则。
证明如下:
根据多元正态分布的密度函数公式得:
两个各取对数,得:
不等式左边展开,得:
因为
协方差矩阵的逆,是对称矩阵,根据矩阵转置的性质,易得:
,继续化简
,
可以改写成:
,替换,最终得:
,取
,协方差矩阵
我们以样本协方差矩阵
代替,即得到:
1.4、案例——LDA算法拓展到贝叶斯
上面我们得到的结论:当两群体来自具有相同协方差矩阵的正态分布时,贝叶斯法则的特殊情形——当![]() (先验概率相同且错分成本相同),等价于LDA分类法则。所以这边我们用Fisher's LDA来做贝叶斯,案例数据集以LDA分类相同。
(先验概率相同且错分成本相同),等价于LDA分类法则。所以这边我们用Fisher's LDA来做贝叶斯,案例数据集以LDA分类相同。
“今天”和“昨天”的湿度差(![]() )和温度差(
)和温度差(![]() )是用来预测“明天”是否会下雨的两个很重要的因素,数据如下;其中label=1表示雨天,label=2表示阴天。
)是用来预测“明天”是否会下雨的两个很重要的因素,数据如下;其中label=1表示雨天,label=2表示阴天。
![]()
![]()
1.4.1、绘制散点图:
plt.scatter(data['Y1'],data['Y2'],c=data['label'])输出:
![]()
1.4.2、假设两群体来自具有相同协方差矩阵的正态分布,用LDA进行贝叶斯分类。
我们基于正态假设,给定一个先验概率priors=[2/3,1/3],然后正常进行LDA分类。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
X=data.iloc[:,:-1] #特征
Y=data.iloc[:,-1] #标签
model_lda= LDA(
priors=[2/3,1/3] #用于LDA中贝叶斯规则的先验概率,当为None时,每个类priors为该类样本占总样本的比例;当为自定义值时,如果概率之和不为1,会按照自定义值进行归一化
)
data_tranform=model_lda.fit_transform(X,Y) #训练模型
#利用模型回测现有样本
Y_predict=model_lda.predict(X) #利用训练的模型回测现有样本
data['label_predict']=Y_predict #保存预测分类结果
data['data_tranform']=data_tranform #降维之后的数据(一维)
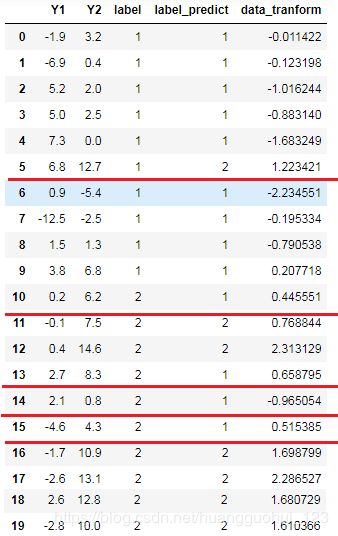
data![]() 输出
输出
其中label_predict是模型预测的分类,我们发现,预测错误的样本还是很多的(这和我们指定的先验概率有关,由于我们的先验概率是随便给的,故预测结果不一定好)。
1.4.3、计算总错分率(TPM):
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict) #1-准确率输出:
0.25错分率为0.25,整体的分类效果不太好。
1.4.4、预测未来数据
如果我们得知今天的数据是![]() ,如何预测明天的天气?
,如何预测明天的天气?
model_lda.predict(pd.DataFrame([[8.0,2.0]]))输出:
array([1], dtype=int64)
即根据给定先验概率的LDA分类法则,预测明天为雨天。
1.5、案例——贝叶斯算法
1.5.1、高斯分布的朴素贝叶斯
除了基于正态假设的LDA算法之外,sklearn中有专门用于先验为高斯分布的朴素贝叶斯的包:naive_bayes.GaussianNB,我们来看看其分类的效果。
from sklearn.naive_bayes import GaussianNB #先验为高斯分布的朴素贝叶斯
X=data.iloc[:,:-1] #特征
Y=data.iloc[:,-1] #标签
model_GNB= GaussianNB(
priors=[2/3,1/3] #用于LDA中贝叶斯规则的先验概率,当为None时,每个类priors为该类样本占总样本的比例;当为自定义值时,如果概率之和不为1,会按照自定义值进行归一化
)
model_GNB.fit(X,Y) #训练模型
#利用模型回测现有样本
Y_predict=model_GNB.predict(X) #利用训练的模型预测分类
data['label_predict']=Y_predict #保存预测分类结果
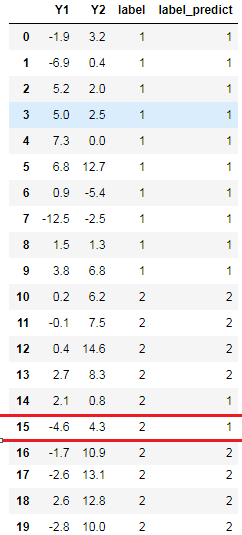
data输出:
1.5.2、计算总错分率(TPM):
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict) #1-准确率输出:
0.1错分率为0.1,在合理的范围之内,可以得出整体的分类效果是不错的。
1.5.3、预测未来数据
如果我们得知今天的数据是![]() ,如何预测明天的天气?
,如何预测明天的天气?
model_lda.predict(pd.DataFrame([[8.0,2.0]]))输出:
array([1], dtype=int64)
即根据贝叶斯分类法则,预测明天为雨天。
二、多分类问题
两样本的贝叶斯分类法则为:
以上分类法则需要考虑误判代价![]() ,多群体的误判代价较为复杂,如果我们有
,多群体的误判代价较为复杂,如果我们有![]() 组,我们需要考虑
组,我们需要考虑![]() 组代价。为了简便起见,我们假设各组具有相同的误判概率,从而简化分类法则:
组代价。为了简便起见,我们假设各组具有相同的误判概率,从而简化分类法则:
![]() :
:![]()
![]() :
:![]()
则推广到多群体贝叶斯分类法则为:将![]() 分到
分到![]() 最大的那个组(其中
最大的那个组(其中![]() 和
和![]() 是先验概率和密度函数,与两群体情况类似)。
是先验概率和密度函数,与两群体情况类似)。
案例:研究团队调查了20个品牌的电视机,记录了它们的市场定位(G):1.高端市场,2. 中端市场,3. 低端市场;质量评估得分(Q),功能评估得分(C)和价格(P,单位为每百元人民币)。如果一个全新的品牌被推出,其中![]() ,它的市场定位应如何?
,它的市场定位应如何?
1、LDA算法拓展到贝叶斯(前提:假设各群体服从正态分布)
1.1、导入数据
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data=pd.read_excel('D:/CDA/dataset/data_LDA&bayers_2.xlsx')
data输出:
![]()
1.2、两两散点图
sns.pairplot(data,hue="G")输出:
![]()
从图中可以看出,以其中的两个指标来划分群体,分类都不是特别明显。
1.3、Fisher's LDA分类(预设先验概率),并利用训练好的模型回测数据
若我们采用贝叶斯法则,假设总体来自正态分布并且错分成本相同,我们可以设置各个总体的先验概率。在此我们可以采用不同的设置方法:①假设3个群体的发生概率是一样的;②数据驱动的方式,以样本的比例来代替先验概率。
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
X=data.iloc[:,:-1] #特征
Y=data.iloc[:,-1] #标签
model_lda_1= LDA(priors=[1/3,1/3,1/3])
model_lda_2= LDA(priors=[5/20,8/20,7/20])
model_lda_1.fit_transform(X,Y) #训练模型
model_lda_2.fit_transform(X,Y) #训练模型
Y_predict_1=model_lda_1.predict(X) #利用训练的模型回测数据
Y_predict_2=model_lda_2.predict(X) #利用训练的模型回测数据
data['label_predict1']=Y_predict_1 #保存预测分类结果
data['label_predict2']=Y_predict_2 #保存预测分类结果
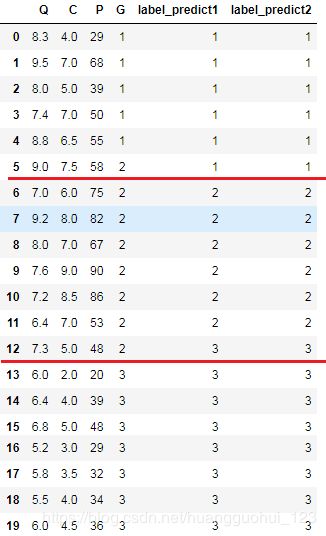
data
输出:
1.4、计算总错分率(TPM):
①各组先验概率相同
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict_1) #1-准确率输出:
0.1②样本比例做先验概率
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict_2) #1-准确率输出:
0.1错分率都为0.1,即前面预设的不同先验概率,在这个问题的分类当中是没有差别的,整体的分类效果是不错的。
1.5、预测未来数据
model_lda_1.predict(pd.DataFrame([[8.0,7.5,65]]))
model_lda_2.predict(pd.DataFrame([[8.0,7.5,65]]))输出:
array([2], dtype=int64)
array([2], dtype=int64)即根据以上分类法则,预测都为中端市场。
2、高斯分布的朴素贝叶斯算法
2.1、高斯分布的朴素贝叶斯算法分类,并利用训练好的模型回测数据
我们可以设置各个总体的先验概率。在此我们可以采用不同的设置方法:①假设3个群体的发生概率是一样的;②数据驱动的方式,以样本的比例来代替先验概率。
from sklearn.naive_bayes import GaussianNB #先验为高斯分布的朴素贝叶斯
X=data.iloc[:,:-1] #特征
Y=data.iloc[:,-1] #标签
model_GNB_1= GaussianNB(priors=[1/3,1/3,1/3])
model_GNB_2= GaussianNB(priors=[5/20,8/20,7/20])
model_GNB_1.fit(X,Y) #训练模型
model_GNB_2.fit(X,Y) #训练模型
#利用模型回测现有样本
Y_predict_1=model_GNB_1.predict(X) #利用训练的模型预测分类
Y_predict_2=model_GNB_2.predict(X) #利用训练的模型预测分类
data['label_predict_1']=Y_predict_1 #保存预测分类结果
data['label_predict_2']=Y_predict_2 #保存预测分类结果
data
输出:
2.2、计算总错分率(TPM):
①各组先验概率相同
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict_1) #1-准确率输出:
0.25②样本比例做先验概率
import sklearn.metrics as sm
1-sm.accuracy_score(Y,Y_predict_2) #1-准确率输出:
0.15错分率分别为0.25和0.15,整体的分类效果不是很好。
1.5、预测未来数据
model_GNB_1.predict(pd.DataFrame([[8.0,7.5,65]]))
model_GNB_2.predict(pd.DataFrame([[8.0,7.5,65]]))输出:
array([2], dtype=int64)
array([2], dtype=int64)即根据以上分类法则,预测都为中端市场。