异质网络表示--Structural Deep Embedding for Hyper-Networks
[Structural Deep Embedding for Hyper-Networks](https://arxiv.org/abs/1711.10146) 是在hyperedge(超边是不可分解的)的基础上保留object的一阶和二阶相似性,学习异质网络表示。于与HEBE的区别在于,本文考虑了网络high-oeder网络结构和高度稀疏性。 传统的基于clique expansion 和star expansion的方法,显式或者隐式地分解网络(如下图所示)。也就说,分解后hyper edge节点地子集,依然可以构成一个新的超边。对于同质网络这个假设是合理地,因为同质网络地超边,大多数情况下都是根据潜在地相似性(共同地标签等)构建的。
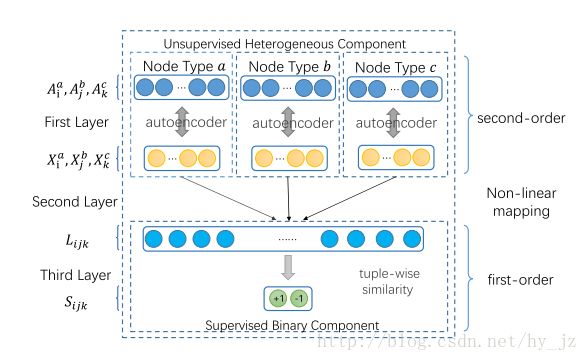
但是在异质网络中要解决两个问题:不可分解性和结构保留。对于不可分解性,作者设计了不可分解的tuplewise相似性函数。这个相似性函数定义在hyper edge的所有节点上,确保超边的子集并没有融合在网络表示中,并且这个函数是非线性的。为了保留网络结构,作者设计了一个 Auto encoder,通过重构节点的邻居结构来学习节点表示,也就说有相似邻居的节点将有相似的向量表示,每一种节点类型对应一个auto encoder。这两部分在模型中,联合优化来同时解决这两个问题。模型框架图如下:
####几个定义 **1. Hyper Network:**一般形式为 G=(V,E) ,有T个类型的节点 V={Vt}Tt=1 ,网络中的边是超边:即可以连接任意数量的节点: E={Ei=(v1,v2,vni)}(ni≥2) 。如果每个超边只连接两个节点,那么就退化为一般的network;如果 T≥2 ,那么就是 heterogeneous hyper-network。 **2. First-Order Similarity:** 一阶相似性衡量的是节点间的N-tuplewise相似性。对于节点 v1,v2,⋯,vN ,如果他们之间存在超边,那么这N个节点的一阶相似性是1,但是这种相似性并不存在于这N个节点的子集上。 **3. Second-Order Similarity:** hyper-network上的二阶相似性,衡量的是节点的邻居结构之间的相似性。邻居指的是: Ei∖vi,ifvi∈Ei 。 #### Loss Function 节点 vi 的向量表示是 Xi ,S表示 N-tuplewise的相似性函数。也就说 1. if (v1,v2,⋯,vN)∈E ,那么 S(v1,v2,⋯,vN) 的值比较大(大于阈值 l)。 2. if (v1,v2,⋯,vN)∉E ,那么 S(v1,v2,⋯,vN) 的值比较小(小于阈值s)。 本文考虑的是N=3的均匀长度的超边。 scoring函数S不可以是线性的。如果是线性的那么: S(v1,v2,⋯,vN)=∑iWiXi 。证明参考论文,基于阈值l和s,举个反例。 对于一阶相似性,本文采用的是multilayer perceptron,分成两个部分。第一部分是模型框架中的第二层,这是个全连接层而且激活函数是非线性的。输入是三个节点 (vi,vj,vk) (他们属于三个不同的节点类型a,b,c)的向量表示 (Xai,Xbj,Xck) 。作者把他们拼接起来,并且映射到统一的空间L。
Lijk=σ(W(2)a∗Xai+W(2)b∗Xbj+W(2)c∗Xck+b(2))
为了得到相似性,把它统一的空间中的表示
Lijk 映射到第三层的概率空间中:
Sijk=S(Xai,Xbj,Xck)=σ(W(3)∗Lijk+b(3))
如果节点
(vi,vj,vk) 之间存在hyper edge,那么
Rijk 的值为1,否则为0。损失函数(1):
L1=−(RijklogSijk+(1−Rijk)log(1−Sijk))
从上式可以看出,如果
Rijk 的值为1,则
Sijk 的值比较大;如果
Rijk 的值为0,则
Sijk 的值比较小。这也就保留了一阶相似性。 **二阶相似性**,跟[SDNE](http://dl.acm.org/citation.cfm?doid=2939672.2939753)的思想是很相似的,也是构造邻接矩阵作为Auto encoder的输入。邻接矩阵
A=HHT−Dv 。矩阵
H 是
|V|×|E| 关联矩阵,每个元素h(v,e)=1,如果节点v属于超边e,否则为0;矩阵
Dv 是对角矩阵,包含着节点的度
d(v)=∑e∈Eh(v,e) 。因而,邻接矩阵的每一项代表着两个节点的共同出现的次数。 Auto encoder包含编码器和解码器。编码器是把输入A非线性映射到X空间,解码器是把X非线性的重构到原始的特征空间
A^ 。
Xi=σ(W(1)Ai+b(1))A^i=σ(W^(1)Xi+b^(1))
Auto Encoder的目的就是最小化输入和输出的重构错误。这就使得有相似邻居结构的节点,向量表示相近,也就是保留了二阶相似性 。邻接矩阵往往是稀疏的,因而作者只是处理非零项,通过sign函数。此外,每个节点类型对应着一个Auto encoder,因而损失函数是:
L2=∑t||sign(Ati)⊙(Ati−A^ti)||2F
为了保留一阶和二阶相似性,论文联合最小化目标函数:
L=L1+αL2
在大多数现实世界的网络中只有正相关关系,所以这个算法收敛时,其中所有的元组关系都是相似的。为了解决这个问题,根据噪声分布,为每条边采样多个负边。整体算法如下:
在实验方面,作者用了四个数据集:
- GPS:超边是(user, location, activity)
- MovieLens:超边是(user, movie, tag)
- drug:超边是(user, drug, reac- tion)
- WordNet:超边是(entity, relation, tail entity)