概率统计——常见分布与假设检验
前言
- P M F PMF PMF:用于二项分布、泊松分布
概率质量函数(Probability Mass Function),用来描述离散型随机变量的分布律。
定义:
假定离散型随机变量 X X X,共有 n n n个取值, X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots ,X_n X1,X2,⋯,Xn,那么 P ( X = X n ) ≥ 0 , ∑ 1 n P ( X = X n ) = 1 P(X=X_n)≥0,\sum_1^nP(X=X_n)=1 P(X=Xn)≥0,1∑nP(X=Xn)=1 - P D F PDF PDF:均匀分布、正态分布、指数分布
概率密度函数(Probability Density Function),用来描述连续型随机变量的分布情况。
之所以引入概率密度函数的概念,是因为连续型随机变量在取固定值的概率时为0,没有意义,故我们讨论某一区间范围内的概率。
定义:
假设连续型随机变量 X X X, f ( x ) f(x) f(x)为概率密度函数,对于任意实数范围如 [ a , b ] [a,b] [a,b],有 P { a ≤ x ≤ b } = ∫ a b f ( x ) d x P\lbrace{a≤x≤b}\rbrace=\int_a^bf(x)dx P{a≤x≤b}=∫abf(x)dx - C D F CDF CDF:
累积分布函数(Cumulative Distribution Function),用来描述连续型随机变量的性质。
在数学上, C D F CDF CDF是 P D F PDF PDF的积分形式。
形式:
累计分布函数为 F ( x ) F(x) F(x),概率密度函数为 f ( x ) f(x) f(x),则 F ( x ) = ∫ − ∞ x f ( x ) d x F(x)=\int_{-\infty}^xf(x)dx F(x)=∫−∞xf(x)dx根据上式可知,累积分布函数 F ( x ) F(x) F(x)在点 x x x处的函数值表示 X X X落在区间 [ − ∞ , x ] [-\infty,x] [−∞,x]内的概率,故累积分布函数就是定义域为 R R R的普通函数。
常见的离散型分布
| 满足条件 | 公式 | 适用场景 | |
|---|---|---|---|
| 二项分布 (Binomial Distribution) |
1、试验次数是固定的; 2、每次试验都是独立的; 3、对于每次试验成功的概率都是一样的。 |
在 n n n次试验中,单次试验成功率为 p p p,失败率为 1 − p 1-p 1−p,则出现成功次数的概率为 P ( X = x ) = C n x p x ( 1 − p ) n − x P(X=x)=C_n^xp^x(1-p)^{n-x} P(X=x)=Cnxpx(1−p)n−x | 1、销售电话成功的次数; 2、一批产品中有缺陷的产品数量; 3、掷硬币正面朝上的次数; 4、在一袋糖果中取糖果吃,拿到红色包装的次数; |
| 泊松分布 (Poisson Distribution) |
1、试验次数 n n n趋向于无穷大; 2、单次事件发生的概率 p p p趋向于0; 3、 n p np np是一个有限的数值。 |
一个服从泊松分布的随机变量 X X X,在具有比例参数(rate parameter) λ ( λ = n p ) \lambda(\lambda=np) λ(λ=np)的一段固定事件间隔内,事件发生次数为 i i i的概率为 P { X = i } = e − λ λ i i ! P\lbrace{X=i}\rbrace=e^{-\lambda}\frac {\lambda^i}{i!} P{X=i}=e−λi!λi | 1、一定时间段内,某航公公司接到的订票电话数; 2、一定时间内,到车站候车的人数; 3、一批布上发现瑕疵点的个数; 4、一定页数的书刊上,发现错别字的个数; |
| 几何分布 (Geometric Distribution) |
考虑独立重复试验,几何分布描述的是经过 k k k次试验才首次获得成功的概率,假定每次成功率为 p p p, P { X = n } = ( 1 − p ) n − 1 p P\lbrace{X=n}\rbrace=(1-p)^{n-1}p P{X=n}=(1−p)n−1p | ||
| 负二项分布 (Negative Binomial Distribution) |
考虑独立重复试验,负二项分布描述的是试验一直进行到成功 r r r次的概率,假定每次成功率为 p p p, P { X = n } = C n − 1 r − 1 p r ( 1 − p ) n − r P\lbrace{X=n}\rbrace=C_{n-1}^{r-1}p^r(1-p)^{n-r} P{X=n}=Cn−1r−1pr(1−p)n−r | ||
| 超几何分布 (Hyper-geometric Distribution) |
超几何分布描述的是在一个总数为 N N N的总体中进行有放回的抽样,其中在总体中 k k k个元素属于一组,剩余 N − k N-k N−k个元素属于另一组,假定从总体中抽取 n n n次,其中包含 x x x个第一组的概率为 P { X = n } = C k x C N − k n − x C N n P\lbrace{X=n}\rbrace=\frac {C_k^xC_{N-k}^{n-x}}{C_N^n} P{X=n}=CNnCkxCN−kn−x |
二项分布、泊松分布、正态分布的联系
当 n n n很大, p p p很小时,如 n ≥ 100 且 n p ≤ 10 n≥100且np≤10 n≥100且np≤10时,二项分布可以近似为泊松分布;
当 λ \lambda λ很大时,如 λ ≥ 1000 \lambda≥1000 λ≥1000时,泊松分布可以近似为正态分布;
当 n n n很大时, n p np np和 n ( 1 − p ) n(1-p) n(1−p)都足够大时,如 n ≥ 100 , n p ≥ 10 , n ( 1 − p ) ≥ 10 n≥100,np≥10,n(1-p)≥10 n≥100,np≥10,n(1−p)≥10时,二项分布可以近似为正态分布。
离散型分布的均值和方差汇总
| 分布 | 均值 | 方差 |
|---|---|---|
| Bernoulli( n n n) (伯努利分布) |
p p p | p ( 1 − p ) p(1-p) p(1−p) |
| Beta-binomial( n , α , β n,\alpha,\beta n,α,β) ( β − 二 项 分 布 \beta-二项分布 β−二项分布) |
n α α + β \frac {n\alpha}{\alpha+\beta} α+βnα | n α β ( α + β ) 2 \frac {n\alpha\beta}{(\alpha+\beta)^2} (α+β)2nαβ |
| Binomial( n , p n,p n,p) (二项分布) |
n p np np | n p ( 1 − p ) np(1-p) np(1−p) |
| Discrete Uniform( N N N) (离散均匀分布) |
N + 1 2 \frac {N+1}{2} 2N+1 | ( N + 1 ) ( N − 1 ) 12 \frac {(N+1)(N-1)}{12} 12(N+1)(N−1) |
| Geometric( p p p) (几何分布) |
1 p \frac {1}{p} p1 | 1 − p p 2 \frac {1-p}{p^2} p21−p |
| Hypergeometric( N , M , K N,M,K N,M,K) (超几何分布) |
K M N \frac {KM}{N} NKM | K M N ( N − M ) ( N − K ) N ( N − 1 ) \frac {KM}{N} \frac {(N-M)(N-K)}{N(N-1)} NKMN(N−1)(N−M)(N−K) |
| Negative Binomial( r , p r,p r,p) (负二项分布/帕斯卡分布) |
r ( 1 − p ) p \frac {r(1-p)}{p} pr(1−p) | r ( 1 − p ) p 2 \frac {r(1-p)}{p^2} p2r(1−p) |
| Poisson( λ \lambda λ) (泊松分布) |
λ \lambda λ | λ \lambda λ |
常见的连续型分布
| 定义及公式 | 例子 | |
|---|---|---|
| 均匀分布 (Uniform Distribution) |
均匀分布指的是一类在定义域内概率密度函数处处相等的统计分布。 若 X X X是服从区间 [ a , b ] [a,b] [a,b]上的均匀分布,则记作 X ~ U [ a , b ] X\text{\textasciitilde}U[a,b] X~U[a,b]。 概率密度函数(PDF): f ( x ) = { 0 , o t h e r s 1 b − a , a ≤ x ≤ b f(x)=\LARGE \lbrace_{0\space\space \space \space \space ,others }^{\frac{1}{b-a},a≤x≤b} f(x)={0 ,othersb−a1,a≤x≤b分布函数: F ( x ) = { 0 , x < a ( x − a ) ( b − a ) , a ≤ x ≤ b 1 , x > b F(x)=\begin{cases}0 \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space ,xb\end{cases} F(x)=⎩⎪⎨⎪⎧0 ,x<a(x−a)(b−a),a≤x≤b1 ,x>b |
1、一个理想的随机数生成器; 2、一个理想的圆盘以一定力度旋转后静止时的角度; |
| 一般正态分布 (Normal Distribution) |
正态分布(高斯分布),是一种对称分布,概率密度成钟摆的形状,记作 X ~ N ( μ , σ 2 ) X\text{\textasciitilde}N(\mu,\sigma^2) X~N(μ,σ2)。 概率密度函数(PDF): f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac {1}{\sqrt {2\pi}\sigma}e^{\frac {-(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e2σ2−(x−μ)2其中, μ \mu μ为均值, σ \sigma σ为标准差。 分布函数: F ( x ) = 1 2 π σ ∫ − ∞ x e − ( t − μ ) 2 2 σ 2 d t F(x)=\frac {1}{\sqrt {2\pi}\sigma}\int_{-\infty}^x e^{\frac {-(t-\mu)^2}{2\sigma^2}}dt F(x)=2πσ1∫−∞xe2σ2−(t−μ)2dt |
1、成人的身高; 2、不同方向的气体分子的运动速度; 3、测量物体质量时的误差; |
| 标准正态分布 | μ = 0 , σ = 1 \mu=0,\sigma=1 μ=0,σ=1时的正态分布。 记作 X ~ N ( 0 , 1 ) 。 X\text{\textasciitilde}N(0,1)。 X~N(0,1)。 概率密度函数(PDF): f ( x ) = 1 2 π e − x 2 2 f(x)=\frac {1}{\sqrt {2\pi}}e^{\frac {-x^2}{2}} f(x)=2π1e2−x2分布函数: F ( x ) = 1 2 π ∫ − ∞ x e − t 2 2 d t F(x)=\frac {1}{\sqrt {2\pi}} \int_{-\infty}^x e^{\frac {-t^2}{2}}dt F(x)=2π1∫−∞xe2−t2dt |
|
| 指数分布 (Exponential Distribution) |
用来描述一个特定事件发生所需要的时间,在指数分布随机变量的分布中,有很少的大数值和非常多的小数值。 记作 X ~ E ( λ ) 。 X\text{\textasciitilde}E(\lambda)。 X~E(λ)。 概率密度函数(PDF): f ( x ) = { λ e − λ x , x ≥ 0 0 , x < 0 f(x)=\begin{cases} \lambda e^{-\lambda x},x≥0 \\ 0 \space \space \space \space \space \space \space \space ,x<0 \end{cases} f(x)={λe−λx,x≥00 ,x<0分布函数: F ( a ) = P { x ≤ a } = 1 − e − λ a , a ≥ 0 F(a)=P\lbrace{x≤a}\rbrace=1-e^{-\lambda a},a≥0 F(a)=P{x≤a}=1−e−λa,a≥0 |
1、顾客到达一家店铺的时间间隔; 2、从现在开始到发生地震的时间间隔; 3、在产线上收到一个有问题产品的时间间隔; |
| Γ \Gamma Γ分布 (Gamma Distribution) |
常用来描述某个事件总共要发生 n n n次的等待时间的分布。 | |
| 威布尔分布 (Weibull Distribution) |
常用来描述在工程领域中某类具有“最弱链”对象的寿命。 |
中心极限定理:
设 X 1 , X 2 , ⋯ X_1,X_2,\cdots X1,X2,⋯是独立同分布的随机变量序列,序列的每一项的均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2,记 Z n = X 1 + X 2 + ⋯ + X n − n μ n σ Z_n=\frac {X_1+X_2+\cdots+X_n-n\mu}{\sqrt {n}\sigma} Zn=nσX1+X2+⋯+Xn−nμ则 Z n Z_n Zn的分布函数的极限分布为标准正态分布函数 Φ ( x ) = 1 2 π ∫ − ∞ x e − z 2 2 d z \Phi(x)=\frac {1}{\sqrt {2\pi}}\int_{-\infty}^xe^{-\frac{z^2}{2}}dz Φ(x)=2π1∫−∞xe−2z2dz即 lim n → ∞ P ( Z n ≤ x ) = Φ ( x ) 对 任 意 的 x 成 立 \lim_{n \to \infty}P(Z_n≤x)=\Phi(x) \space \space \space \space \space \space \space \space 对任意的x成立 n→∞limP(Zn≤x)=Φ(x) 对任意的x成立
中心极限定理是一个非常具有一般性的定理。对于中心极限定理的条件:
1、序列为独立同分布;
2、假设各项的均值和方差的有限性;
3、 X i X_i Xi的分布可以是离散的、连续的、混合的。从理论角度看:
该定理表明大样本的独立随机变量序列和大致是正态的。
当我们遇到的随机量是由许多影响小但是独立的随机因素的总和的情况,根据中心极限定理就可以判定这个随机量的分布是正态的。
从应用角度看:
不需要考虑随机变量具体服从什么分布,从而避免了繁琐的分布列和概率密度函数的计算。
计算过程中,只需要知道均值、方差、标准正态分布表即可。基于中心极限定理的正态近似:
本质是**将 Z n Z_n Zn的分布近似看成正态分布。
因为正态分布在线性变换下仍然是正态分布,所以将 S n S_n Sn视为均值为 n μ n\mu nμ,方差为 n σ 2 n\sigma^2 nσ2的正态随机变量。
令 S n = X 1 + X 2 + ⋯ + X n S_n=X_1+X_2+\cdots+X_n Sn=X1+X2+⋯+Xn,其中 X 1 + X 2 + ⋯ + X n X_1+X_2+\cdots+X_n X1+X2+⋯+Xn是独立同分布的随机变量序列(均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2)。当 n n n充分大时,概率 P ( S n ≤ c ) P(S_n≤c) P(Sn≤c)可以通过将 S n S_n Sn视为正态随机变量来近似计算,步骤如下:
1、计算 S n S_n Sn的均值 n μ n\mu nμ和方差 n σ 2 n\sigma^2 nσ2;
2、计算归一化后的值 z = c − n μ n σ z=\frac {c-n\mu}{\sqrt {n}\sigma} z=nσc−nμ;
3、计算近似值 P ( S n ≤ c ) ≈ Φ ( z ) , P(S_n≤c)\thickapprox\Phi(z), P(Sn≤c)≈Φ(z),其中 Φ ( z ) \Phi(z) Φ(z)可以从标准正态分布表差得。
例题(中心极限定理近似正态)
飞机上运载100件包裹,每件包裹的重量是独立的随机变量,且在5磅到50磅之间均匀分布。那么这100件包裹的总重量超过3000磅的概率是多少?
【直接计算总重量的分布,从未计算该概率是非常不容易的。但是使用中心极限定理可以很容易计算该概率的近似值。】
解:
计算 P ( S 100 > 3000 ) P(S_{100}>3000) P(S100>3000),其中 S 100 S_{100} S100是这100件包裹的总重量。
每件包裹的平均重量和方差是: μ = 5 + 50 2 = 27.5 , σ 2 = ( 50 − 5 ) 12 = 168.75 \mu=\frac {5+50}{2}=27.5,\sigma^2=\frac {(50-5)}{12}=168.75 μ=25+50=27.5,σ2=12(50−5)=168.75然后计算标准正态值: z = 3000 − 100 × 27.5 100 × 168.75 = 250 129.9 = 1.92 z=\frac {3000-100×27.5}{\sqrt {100×168.75}}=\frac {250}{129.9}=1.92 z=100×168.753000−100×27.5=129.9250=1.92使用标准正态近似,可以得到: P ( S 100 ≤ 3000 ) ≈ Φ ( 1.92 ) = 0.9726 P(S_{100}≤3000)\thickapprox\Phi(1.92)=0.9726 P(S100≤3000)≈Φ(1.92)=0.9726所以 P ( S 100 > 3000 ) = 1 − P ( S 100 ≤ 3000 ) ≈ 1 − 0.9726 = 0.0274 P(S_{100}>3000)=1-P(S_{100}≤3000)\thickapprox1-0.9726=0.0274 P(S100>3000)=1−P(S100≤3000)≈1−0.9726=0.0274
连续型分布的均值和方差汇总
| 分布 | 均值 | 方差 |
|---|---|---|
| Exponential( θ \theta θ) (指数分布) |
θ \theta θ | θ 2 \theta^2 θ2 |
| Gamma( α , β \alpha,\beta α,β) | α β \alpha\beta αβ | α β 2 \alpha \beta^2 αβ2 |
| Normal( μ , σ 2 \mu,\sigma^2 μ,σ2) (正态分布) |
μ \mu μ | σ 2 \sigma^2 σ2 |
| Uniform(a,b) (均匀分布) |
b + a 2 \frac {b+a}{2} 2b+a | ( b − a ) 2 2 \frac {(b-a)^2}{2} 2(b−a)2 |
代码实现
生成一组符合特定分布的随机数
import numpy
#生成大小为1000的符合b(10,0.5)二项分布的样本集
s_binomial = numpy.random.binomial(n=10,p=0.5,size=1000)
#生成大小为1000的符合P(1)的泊松分布的样本集
s_poisson = numpy.random.poisson(lam=1,size=1000)
#生成大小为1000的符合U(0,1)均匀分布的样本集,此方法的边界值为左闭右开区间
s_unifrom = numpy.random.uniform(low=0,high=1,size=1000)
#生成大小为1000的符合N(0,1)的正态分布的样本集
#normal函数为一般正态分布,自定义均值和标准差
#standard_normal函数是标准正态分布
s_normal = numpy.random.normal(loc=0,scale=1,size=1000)
s_standard_normal = numpy.random.standard_normal(size=1000)
#生成大小为1000的符合E(1/2)指数分布的样本集,参数为λ的倒数
s_exp = numpy.random.exponential(scale=2,size=1000)
计算统计分布的PDF、PMF、CDF
from scipy import stats
import numpy
#计算二项分布B(10,0.5)的PMF
x = range(11)
p = stats.binom.pmf(x,n=10,p=0.5)
#计算泊松分布P(1)的PMF
x = range(11)
p = stats.poisson.pmf(x,mu=1)
#计算均匀分布U(0,1)的PDF
x = numpy.linspace(0,1,100)
p = stats.uniform.pdf(x,loc=0,scale=1)
#计算指数分布E(1)的PDF
x = numpy.linspace(0,10,1000)
p = stats.expon.pdf(x,loc=0,scale=1)
#只需要将上述的pmf和pdf替换成cdf即可
#以正态分布为例,计算正态分布N(0,1)CDF
x = numpy.linspace(-3,3,1000)
p = stats.norm.cdf(x,loc=0,scale=1)
统计分布可视化
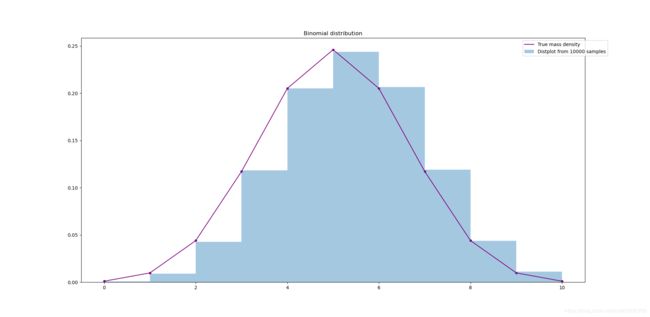
二项分布:
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
#二项分布成功的次数(x轴)
x = range(11)
#B(10,0.5)随机抽样10000次
t = stats.binom.rvs(10,0.5,size=10000)
#B(10,0.5)真实概率质量
p = stats.binom.pmf(x,10,0.5)
fig, ax = plt.subplots(1,1)
sns.distplot(t,bins=10,hist_kws={'density':True},kde=False,label='Distplot from 10000 samples')
sns.scatterplot(x,p,color='purple')
sns.lineplot(x,p,color='purple',label='True mass density')
plt.title('Binomial distribution')
plt.legend(bbox_to_anchor=(1.05,1))
plt.show()
假设检验
假设检验基本概念:
在总体的分布函数完全未知或只知其形式,不知其参数的情况下,为了推断总体的某些未知特性,提出某些关于总体的假设。
假设检验的基本步骤:
| 步骤 | 概念 |
|---|---|
| step1: 陈述研究假设,包含原假设(Null Hypothesis)和备择假设(Alternate Hypothesis) |
原假设: 变量之间不存在某种差异或关联。 备择假设: 变量之间存在某种差异或关联。 |
| step2: 为验证假设收集数据 |
为了确保检验的结果真实可靠,需要根据实际的假设命题从总体中抽取样本,且抽取的数据必须具有代表性, |
| step3: 构造合适的统计测试量并测试 |
所有统计检验都是基于组内方差和组间方差的比较。 如果组间方差足够大,使得不同组之间几乎没有重叠,那么统计量会反映出一个非常小的 P P P值,意味着不同组之间的差异不可能有偶然性导致。 |
| step4: 决定是接受还是拒绝原假设 |
通常以 P = 0.05 P=0.05 P=0.05作为临界值。(单侧检验) |
| step5: 展示结论 |
统计量的选择:
最常用的统计检验有三类:
- 回归检验:(Regression test):适用于预测变量是数值型的情况。
- 比较检验(Comparison test):适用于预测变量是类别型,结果变量是数值型的情况。
- 关联检验(Correlation test):主要是卡方检验,适用于预测变量和结果变量都是类别型的情况。
满足前提条件:样本之间独立、不同组的组内方差近似、数据满足正态性。
| 回归检验 | 预测变量 | 结果变量 |
|---|---|---|
| 简单线性回归 | 单个,连续数值 | 连续数值 |
| 多重线性回归 | 多个,连续数值 | 连续数值 |
| Logistic回归 | 连续数值 | 二元类别 |
| 比较检验 | 预测变量 | 结果变量 |
|---|---|---|
| Paried t-test | 两组,类别 | 组来自同一总体,数值 |
| Independent t-test | 两组,类别 | 组来自不同总体,数值 |
| ANOVA | 两组及以上,类别 | 单个,数值 |
| MANOVA | 两组及以上,类别 | 两个及以上,数值 |
前提条件不满足时,采用非参数检验:
| 非参数检验 | 用于替代的参数检验 |
|---|---|
| Spearman | 回归和关联检验 |
| Sign test | T-test |
| Kruskal-Wallis | ANOVA |
| ANOSIM | MANOVA |
| Wilcoxon Rank-Sum test | Independent t-test |
| Wilcoxon Signed-rank test | Paried t-test |
理论上,进行假设检验时,错误是无法完全避免的,根据定义,错误分为两类。
- 一类错误(type Ⅰ error):拒绝真的原假设。
可以通过 α \alpha α(显著性水平)值来控制,它对一类错误有直接影响;
α \alpha α可以被认为是我们犯一类错误的最大可能性;
以95%的置信水平为例, α \alpha α=0.05,我们犯一类错误的可能性是5%; - 二类错误(type Ⅱ error):接受错误的原假设。
通常由小样本或高样本方差导致;
错误率用 β \beta β表示,二类错误不能通过设置错误率来控制;
可以通过功效角度分析,进行功效分析(Power Analysis)计算出功效值 1 − β 1-\beta 1−β - 两种错误不能同时降低,降低一类的同时会提高二类,至于如何平衡,取决于我们更能接受哪一类。