剑指 offer 面试题精选图解 12. 矩阵中的路径
点击关注上方“图解面试算法”,
设为“置顶或星标”,一起刷 LeetCode。
![]()
作者:景禹
题目描述
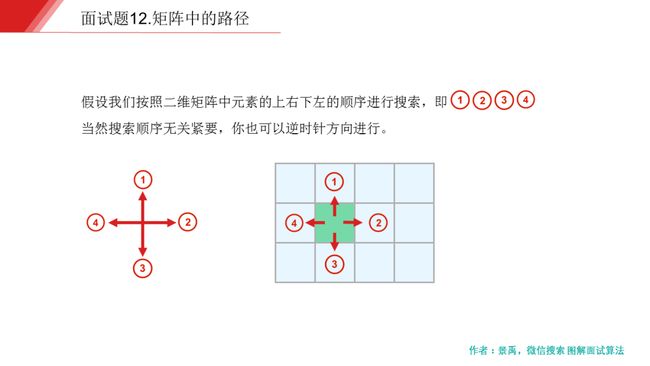
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的 3×4 的矩阵中包含一条字符串 “bfce” 的路径(路径中的字母用加粗标出)。
[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]
但矩阵中不包含字符串 “abfb” 的路径,因为字符串的第一个字符 b 占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例1
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true
示例2
输入:board = [["a","b"],["c","d"]], word = "abcd" 输出:false
题目解析
题目考察的知识点就是深度优先搜索,在一个二维矩阵中判断是否存在单词 word 的一条路径,先从二维矩阵中选择一个任意一个起点,然后从该起点进行深度优先遍历。看下图就会更清晰:
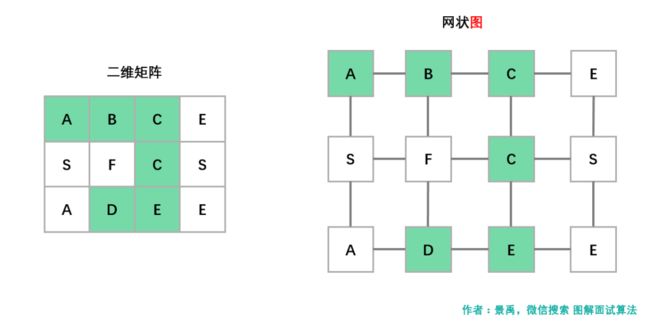
二维矩阵在本质上你可以将其看做一个网状的图,而关于图上面的深度优先搜索,我想你应该很清楚,不论是 DFS 还是 BFS 的实现方式,最简单的就是递归,只不过对于这样一个网状图而言,我们需要将图中的每一个顶点作为起点,并根据给定的 word 都进行一次深度优先搜索,相比于图的一次遍历复杂了些,判断条件也相应的多了些,仔细结合视频动画和代码理解起来就会相当容易。
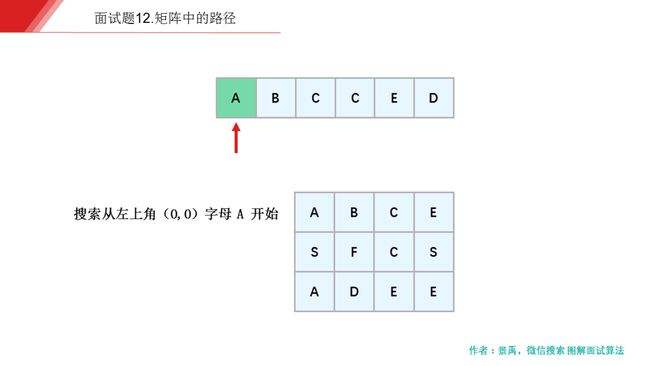
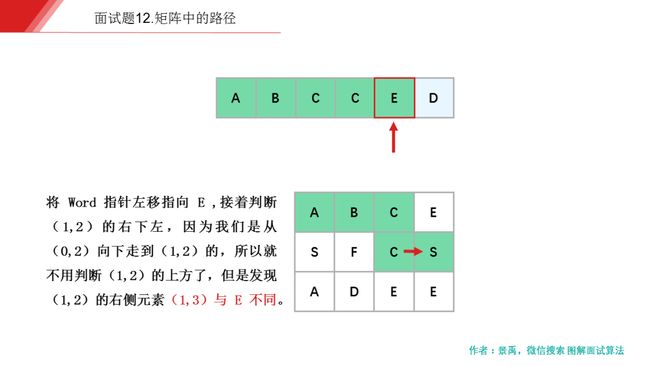
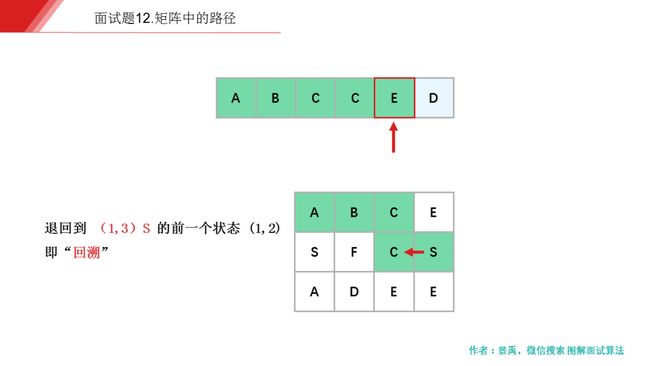
下面是示例一的一个具体解释:
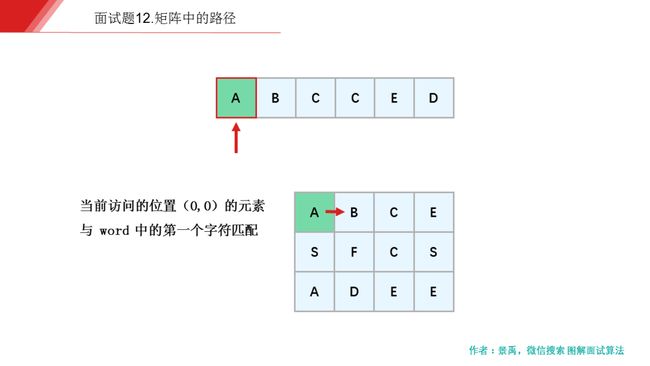
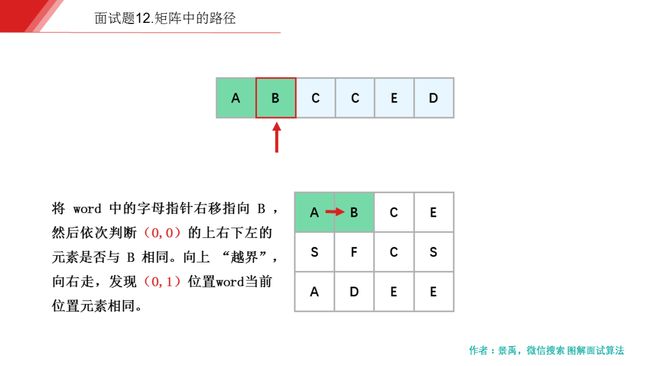
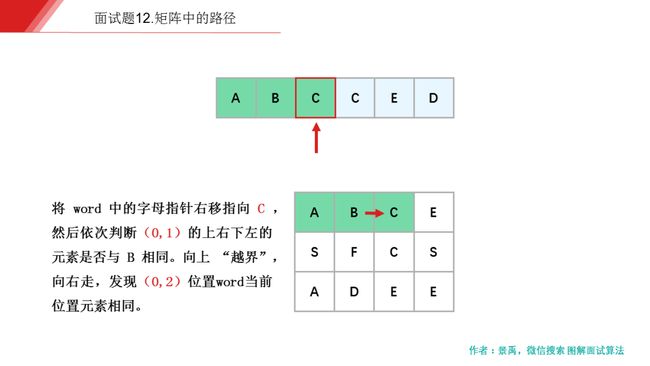
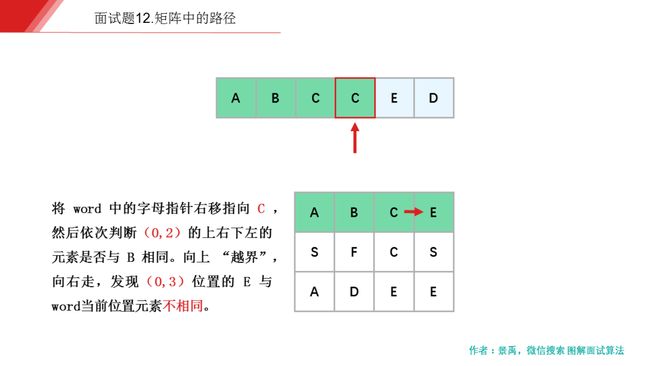
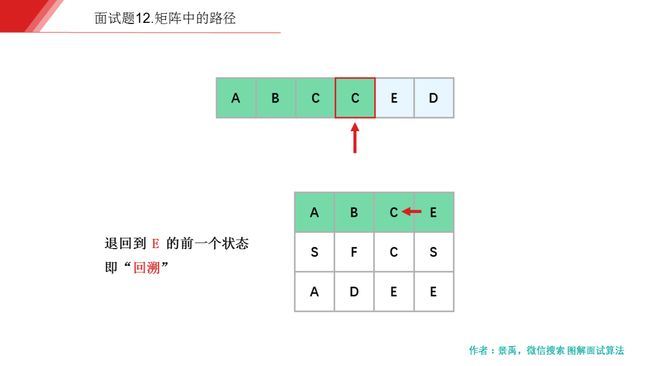

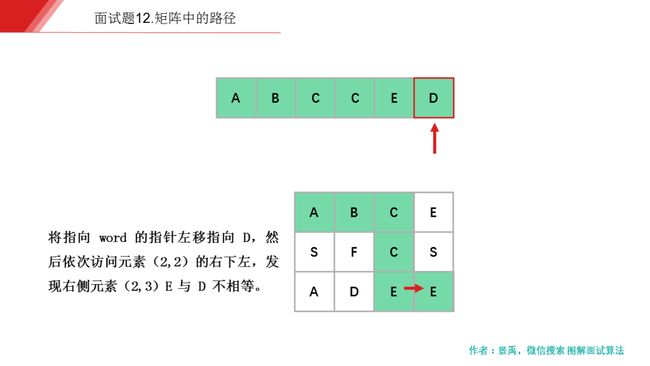
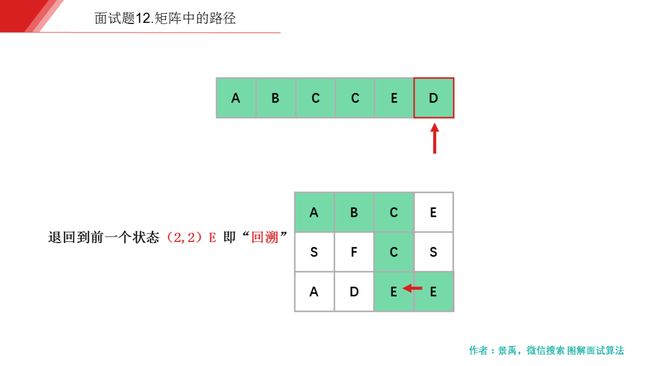
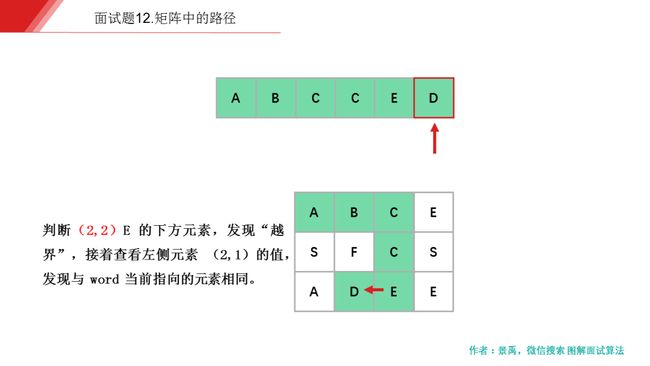
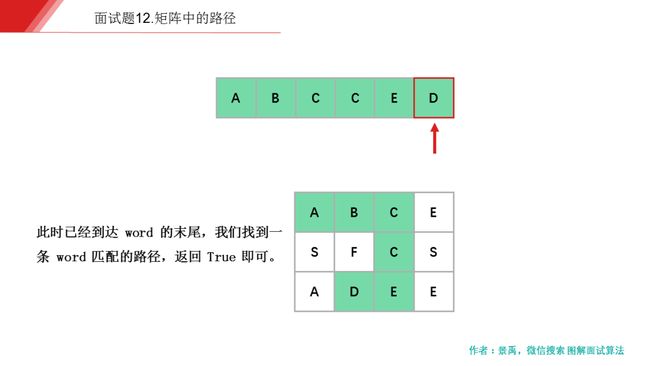
动画描述
代码实现
bool hasPath(const char* matrix, int rows, int cols, const char* str)
{
if(matrix == nullptr || rows < 1 || cols < 1 || str == nullptr)
return false;
bool *visited = new bool[rows * cols];
memset(visited, 0, rows * cols);
int pathLength = 0;
for(int row = 0; row < rows; ++row)
{
for(int col = 0; col < cols; ++col)
{
if(hasPathCore(matrix, rows, cols, row, col, str,
pathLength, visited))
{
return true;
}
}
}
delete[] visited;
return false;
}
bool hasPathCore(const char* matrix, int rows, int cols, int row,
int col, const char* str, int& pathLength, bool* visited)
{
if(str[pathLength] == '\0')
return true;
bool hasPath = false;
if(row >= 0 && row < rows && col >= 0 && col < cols
&& matrix[row * cols + col] == str[pathLength]
&& !visited[row * cols + col])
{
++pathLength;
visited[row * cols + col] = true;
hasPath = hasPathCore(matrix, rows, cols, row, col - 1,
str, pathLength, visited)
|| hasPathCore(matrix, rows, cols, row - 1, col,
str, pathLength, visited)
|| hasPathCore(matrix, rows, cols, row, col + 1,
str, pathLength, visited)
|| hasPathCore(matrix, rows, cols, row + 1, col,
str, pathLength, visited);
if(!hasPath)
{
--pathLength;
visited[row * cols + col] = false;
}
}
return hasPath;
}
时间复杂度
不论如何都要遍历二维矩阵一遍,即 ,对二维矩阵中的每一个顶点作为起点,最深的路径为 word 中单词的长度 ,所以最坏情况下的时间复杂度为 .
知识点
深度优先搜索 DFS ,递归
---
由 五分钟学算法 原班人马打造的公众号:图解面试算法,现已正式上线!
接下来我们将会在该公众号上,为大家分享优质的算法解题思路,坚持每天一篇原创文章的输出,感兴趣的小伙伴可以关注一下哈!