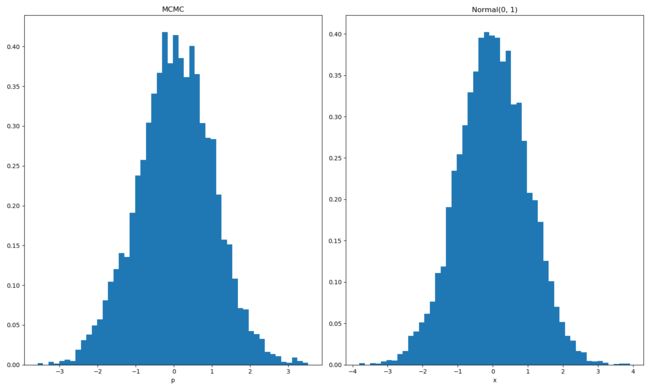
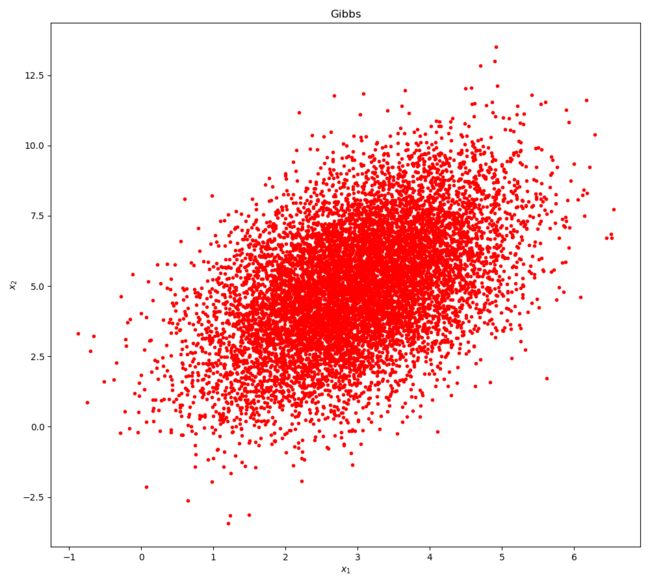
'''' 假设目标分布是: 一维的正太分布, i.e., N(0, 1) 建议的转移矩阵Q(i,j)也是正太分布, j 服从 N(i, 2^2) pi(i)Q(i,j)*alpha(i,j) = pi(j)Q(i,j)*alpha(i,j) where alpha(i,j) = pi(j)Q(j,i) 接受率 alpha(i,j) 可能很小,导致接受率比较小,采样效率低下 修正: alpha(i,j) = min(1, alpha(i,j ) / alpha(j, i)) = min(1, pi(j)Q(j,i) / pi(i)Q(i,j)) = min(1, pi(j) / pi(i)) # 通常Q(i,j)是对称的, 并且此时分布pi都无需归一化 Gibbs采样: 考虑二维的情况, A = (x1, y1), B = (x1, y2), C = (x2, y2) 那么有: pi(A)pi(B|A) = p(x1)p(y1|x1) * p(y2|x1) pi(B)pi(A|B) = p(x1)p(y2|x1) * p(y1|x1) 上面两个式子相等: ==> pi(A)*p(y2|x1) = pi(B)*p(y1|x1), A和B具有相同的x坐标x1 同理,我们有 pi(B)*p(x2|y2) = pi(C)*p(x1|y2), B和C具有相同的y坐标y2 因此,我们可以构造出接受率为1的状态转移矩阵,如上定义,沿着某个坐标轴进行采样,其余坐标保持不变 高维的情况类似 ''' from scipy import stats import numpy as np import matplotlib.pyplot as plt def MCMC_01(): def target_pdf(x): return stats.norm.pdf(x, loc=0, scale=1) # 随机变量的概率密度函数 X_0 = 2.0 Sample_X = [X_0] for t in range(100000): X_i = Sample_X[-1] X_j = np.random.randn() * 2 + X_i # 服从分布 N(i, 2) alpha = min(1, target_pdf(x=X_j) / target_pdf(x=X_i)) p = np.random.rand() if p < alpha: #接受 Sample_X.append(X_j) else: Sample_X.append(X_i) show_cnt = 10000 Sample_X = Sample_X[-show_cnt:] Standard_X = np.random.randn(show_cnt) plt.figure(figsize=(15, 9)) plt.subplot(1, 2, 1) plt.hist(Sample_X, bins=50, normed=1) plt.xlabel('x') plt.xlabel('p') plt.title('MCMC') plt.subplot(1, 2, 2) plt.hist(Standard_X, bins=50, normed=1) plt.xlabel('x') plt.title('Normal(0, 1)') plt.show() MCMC_01() def MCMC_02(): ''' 目标分布是二维的正太分布:N (u, sigma^2), u= (u1, u2) = (3, 5), sigma = [[sigma_1^2, rho*sigma_1*sigma_2], [rho*sigma_1*sigma_2, sigma_2^2]] = [[1, 2], [2, 4]] 那么对应的条件分布为: P(x1|x2) = N(u1 + (x2 - u2) * rho * sigma_1 / sigma_2, (1-rho^2) * sigma_1^2) P(x2|x1) = N(u2 + (x1 - u1) * rho * sigma_2 / sigma_1, (1-rho^2) * sigma_2^2) ''' u1, u2 = 3, 5 sigma_1, sigma_2, rho = 1, 2, 0.5 def gibbs_sampling_x2_given_x1(x1): # return: p(x2|x1) now_u = u2 + (x1 - u1) * rho * sigma_2 / sigma_1 now_sigma = np.sqrt(1 - rho ** 2) * sigma_2 ** 2 now_sigma = np.sqrt(now_sigma) return np.random.randn() * now_sigma + now_u def gibbs_sampling_x1_given_x2(x2): # return: p(x1|x2) now_u = u1 + (x2 - u2) * rho * sigma_1 / sigma_2 now_sigma = (1-rho ** 2) * sigma_1 ** 2 now_sigma = np.sqrt(now_sigma) return np.random.randn() * now_sigma + now_u X_0 = [-2.0, -3.0] Sample_X = [X_0] for t in range(100000): x_2_pre = Sample_X[-1][-1] x_1 = gibbs_sampling_x1_given_x2(x2=x_2_pre) #根据上一个采样点的x2, 采样现在的x1 x_2 = gibbs_sampling_x2_given_x1(x1=x_1) #根据刚刚采样点的x1, 采样现在的x2 Sample_X.append([x_1, x_2]) if t<10: print('x_1:{} x_2:{}'.format(x_1, x_2)) show_cnt = 10000 Sample_X = np.array(Sample_X[-show_cnt:]) # Standard_X = np.random.randn(show_cnt) print('Sample_X:', Sample_X.shape) plt.figure(figsize=(10, 9)) plt.subplot(1, 1, 1) plt.plot(Sample_X[:, 0], Sample_X[:, 1], 'r.') plt.xlabel('$x_1$') plt.ylabel('$x_2$') plt.title('Gibbs') plt.show() MCMC_02()