字符串匹配(BF,KMP,BM)
一.暴力匹配法
最原始,最直观的办法,就是蛮力搜索法,思路是这样子的,需要在str1中寻找str2,那么可以先在str1中查找str2[0],如果找到,则比较往后的字符,
如果全匹配,则返回一开始的符号,如果不匹配,继续在str1中找str2[0],一直重复以上步骤,直至找到为止.分析这种办法的时间复杂度.在最差的情
况下,例如长度为m的字符串0000000000,和长度为n的字符串00001,那么显然时间效率为o(mn).在这里我们可以知道,具体的代码实现应该需
要双层嵌套.(这种直觉往往能带来帮助).外层用来扫描str1,内层用来实现str2.代码如下:
int Match1(char* str1,char* str2)
{
int j=0;
for(int i=0;str1[i] != '\0';++i)
{
while( str2[j] != '\0' &&str1[i+j] !='\0' && str1[i+j] == str2[j])
++j;
if(str2[j]=='\0')
return i;
j=0;
}
return -1;
}为了和KMP算法对比,写成以下形式
int Match2(char* str1,char* str2)
{
int i=0,j=0;
while(str1[i] !='\0' && str2[j] != '\0')
{
if(str1[i] == str2[j])//匹配
{
++i;
++j;
}
else
{
i=i-j+1;//回退str1的指针
j=0;//str2从0开始
}
}
if(str2[j] == '\0')
return i-j;//匹配成功
else
return -1;
}
二.KMP算法
转载自一篇比较浅显易懂的文章:点击打开链接
字符串匹配是计算机的基本任务之一。
举例来说,有一个字符串"BBC ABCDAB ABCDABCDABDE",我想知道,里面是否包含另一个字符串"ABCDABD"?
许多算法可以完成这个任务,Knuth-Morris-Pratt算法(简称KMP)是最常用的之一。它以三个发明者命名,起头的那个K就是著名科学家
Donald Knuth。这种算法不太容易理解,网上有很多解释,但读起来都很费劲。直到读到Jake Boxer的文章,我才真正理解这种算法。
下面,我用自己的语言,试图写一篇比较好懂的KMP算法解释。
1.
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,
所以搜索词后移一位。
2.
因为B与A不匹配,搜索词再往后移。
3.
就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
4.
接着比较字符串和搜索词的下一个字符,还是相同。
5.
直到字符串有一个字符,与搜索词对应的字符不相同为止。
6.
这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置
"移到已经比较过的位置,重比一遍。
7.
一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,
不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
8.
怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,
这里只要会用就可以了。
9.
已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照
下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
10.
因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,
于是将搜索词向后移2位。
11.
因为空格与A不匹配,继续后移一位。
12.
逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
13.
逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,
这里就不再重复了。
14.
下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,
一个字符串的全部尾部组合。
15.
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
16.
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
(完)
下面转自:点击打开链接
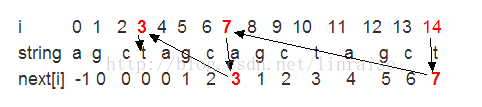
1、用一个例子来解释,下面是一个子串的next数组的值,可以看到这个子串的对称程度很高,所以next值都比较大。
| 位置i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 前缀next[i] |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
4 |
0 |
| 子串 |
a |
g |
c |
t |
a |
g |
c |
a |
g |
c |
t |
a |
g |
c |
t |
g |
申明一下:下面说的对称不是中心对称,而是中心字符块对称,比如不是abccba,而是abcabc这种对称。
(1)逐个查找对称串。
这个很简单,我们只要循环遍历这个子串,分别看前1个字符,前2个字符,3个... i个 最后到15个。
第1个a无对称,所以对称程度0
前两个ag无对称,所以也是0
依次类推前面0-4都一样是0
前5个agcta,可以看到这个串有一个a相等,所以对称程度为1前6个agctag,看得到ag和ag对成,对称程度为2
这里要注意了,想是这样想,编程怎么实现呢?
只要按照下面的规则:
a、当前面字符的前一个字符的对称程度为0的时候,只要将当前字符与子串第一个字符进行比较。这个很好理解啊,前面都是0,说明都不对称了,如果多加了一个字符,要对称的话最多是当前的和第一个对称。比如agcta这个里面t的是0,那么后面的a的对称程度只需要看它是不是等于第一个字符a了。
b、按照这个推理,我们就可以总结一个规律,不仅前面是0呀,如果前面一个字符的next值是1,那么我们就把当前字符与子串第二个字符进行比较,因为前面的是1,说明前面的字符已经和第一个相等了,如果这个又与第二个相等了,说明对称程度就是2了。有两个字符对称了。比如上面agctag,倒数第二个a的next是1,说明它和第一个a对称了,接着我们就把最后一个g与第二个g比较,又相等,自然对称成都就累加了,就是2了。
c、按照上面的推理,如果一直相等,就一直累加,可以一直推啊,推到这里应该一点难度都没有吧,如果你觉得有难度说明我写的太失败了。
当然不可能会那么顺利让我们一直对称下去,如果遇到下一个不相等了,那么说明不能继承前面的对称性了,这种情况只能说明没有那么多对称了,但是不能说明一点对称性都没有,所以遇到这种情况就要重新来考虑,这个也是难点所在。
(2)回头来找对称性
这里已经不能继承前面了,但是还是找对称程度,最愚蠢的做法大不了写一个子函数,查找这个字符串的最大对称程度,怎么写方法很多吧,比如查找出所有的当前字符串,然后向前走,看是否一直相等,最后走到子串开头,当然这个是最蠢的,我们一般看到的KMP都是优化过的,因为这个串是有规律的。
在这里依然用上面表中一段来举个例子:
位置i=0到14如下,我加的括号只是用来说明问题:
(a g c t a g c )( a g c t a g c) t
我们可以看到这段,最后这个t之前的对称程度分别是:1,2,3,4,5,6,7,倒数第二个c往前看有7个字符对称,所以对称为7。但是到最后这个t就没有继承前面的对称程度next值,所以这个t的对称性就要重新来求。
这里首要要申明几个事实
1、t 如果要存在对称性,那么对称程度肯定比前面这个c 的对称程度小,所以要找个更小的对称,这个不用解释了吧,如果大那么t就继承前面的对称性了。
2、要找更小的对称,必然在对称内部还存在子对称,而且这个t必须紧接着在子对称之后。
如下图说明。
从上面的理论我们就能得到下面的前缀next数组的求解算法。
void SetPrefix(const char *Pattern, int prefix[])
{
int len=CharLen(Pattern);//模式字符串长度。
prefix[0]=0;
for(int i=1; iKMP总结
下面是我根据上面两篇博客和数据结构-严蔚敏一书得出的一些心得体会.
KMP算法的核心是next数组的构造.next数组的构造本质上就是查找首尾对称的最长子串长度.
void getNext()
初始化:next[0]=-1,next[1]=0.
假设next[i] == j,则p[0…j-1]=p[i-j…i-1],.那么求next[i+1]有两种情况:
1)如果p[j]=p[i],则p[0…j]=p[i-j…i],所以next[i+1]=j+1=next[i]+1;
2)如果p[j]!=p[i],(难点)
解释:
如果p[j]!=p[i],则说明i+1号元素的对称子串比i号元素的对称子串要短.
看上面的(2)回头来找对称性 我们可以得到启发:
举例:
(a g c t a g c )( a g c t a g c) t
1.t如果要存在对称性,那么对称程度肯定比前面这个c的对称程度小,所以要找个更小的对称,因为如果大,那么t就继承前面的对称性了。
2.要找更小的对称,必然在对称内部还存在子对称,而且这个t必须紧接着在子对称之后。
上面的图示找最长对称子串的步骤:
14号元素是t, next[14]=7,判断string[14] == string[7] (a != t)不成立,继续递归下降查找.
next[7]=3,判断string[14]==string[3],成立,则找到了最长子串.
由上面的分析,我们可以知道,"在内部对称中寻找更小的内部对称,就是递归下降的思想,因此是可以用递归来求解的"
getNext()函数的理解难点是j=next[j]的递归下降查找,由上图就可以清晰地理解.
特点:KMP的串如何存在对称,则肯定是嵌套对称,即大的对称串中必然存在小的对称串,所以可以从大的对称串递归下降地求小的对称串.
KMP算法完整测试代码
#include
using namespace std;
void getNext(const char *p,int *next)
{
int i,j;
next[0]=-1;
i=0;
j=-1;
while(i<(signed)strlen(p)-1)
{
if(j==-1||p[i]==p[j]) //1.j==-1说明不再有子对称,则next[i+1]=0
{ //2.匹配的情况下,p[j]==p[k],则next[i+1]=j+1;
i++;
j++;
next[i]=j;
}
else //while(j!=-1 && p[i]!=p[j]),一直递归查找,化整为零
j=next[j]; //一直在对称内部中查找子对称,直至不再有子对称(j==-1),或者p[i]==p[j]时,就更可以更新next[i+1]
}
}
int KMP(const char * s, const char *p)
{
int slen=strlen(s),plen=strlen(p);
int *next = (int*)malloc(sizeof(int)*plen);
getNext(p,next);
int i=0,j=0;
while(i 实训:http://acm.hdu.edu.cn/showproblem.php?pid=1358
这个题主要考察kmp算法中next数组的应用,大致思路是这样的:求出next数组后(next[0]~next[len]),从i=2(也就是第三个 字符)开始,
令j=i-next[i],j可以整除i,则说明存在,输出i和i/j;为什么要这样做呢,j=i-next[i]就是看i和next[i] 之间有多少个字母,如果i%j==0,
则说明i之前一定有一个周期性的字串,长度为i-j,次数为i/j.例如:aabaabaabaab
#include
#include
char pattern[1000001];
int next[1000001];
int len;
void getNext()
{
int i=0,j=-1;
next[0]=-1;
while( i < len )
{
if( j == -1 || pattern[j] == pattern[i] )
{
++i,++j;
next[i]=j;
}
else
{
j=next[j];
}
}
}
int main()
{
int t=1,i,j;
while(scanf("%d",&len)&&len)
{
getchar();
scanf("%s",pattern);
getNext();
printf("Test case #%d\n",t++);
for(i=2;i<=len;i++)
{
j=i-next[i];
if(i%j==0)
{
if(i/j>1) printf("%d %d\n",i,i/j);
}
}
printf("\n");
}
return 0;
} 实训:HDU1711:http://acm.hdu.edu.cn/showproblem.php?pid=1711
完全的KMP.
#include
using namespace std;
int next[10005],pLen,sLen;
int str[1000000],pattern[10005];
void getNext()
{
int i=0,j=-1;
next[0]=-1;
while( i < pLen )
{
if( j==-1 || pattern[i] == pattern[j])
{
++i,++j;
next[i]=j;
}
else
{
j=next[j];
}
}
}
int KMP()
{
int i=0,j=0;
getNext();
while( i < sLen && j < pLen )
{
if( j== -1 || str[i] == pattern[j] )
{
++i;
++j;
}
else
{
j=next[j];
}
}
if( j == pLen )
return i-j+1;
else
return -1;
}
int main()
{
int T,i;
cin>>T;
while(T--)
{
cin>>sLen>>pLen;
for(i=0;i>str[i];
for(i=0;i>pattern[i];
cout< BM算法
来源:点击打开链接,个中内容有改动
后缀匹配,是指模式串的比较从右到左,模式串的移动也是从左到右的匹配过程,经典的BM算法其实是对后缀蛮力匹配算法的改进。
所以还是先从最简单的后缀蛮力匹配算法开始。下面直接给出伪代码,注意这一行代码:j++;BM算法所做的唯一的事情就是改进了这行代码,
即模式串不是每次移动一步,而是根据已经匹配的后缀信息,从而移动更多的距离。
int Match(const char* pDest, int nDLen, const char* pPattern, int nPLen)
{
if (0 == nPLen)//空字符返回-1
return -1;
int nDstart = nPLen-1;
while (nDstart < nDLen)
{
int suffLen = 0;//统计好后缀的长度
while (suffLen < nPLen && pDest[nDstart-suffLen] == pPattern[nPLen-1-suffLen])
++suffLen ;
if (suffLen == nPLen)
{
return nDstart - (nPLen-1);//匹配
}
++nDstart;
}
return -1;
}
为了实现更快地移动模式串,BM算法定义了两个规则,好后缀规则和坏字符规则,如下图可以清晰的看出他们的含义。
利用好后缀和坏字符可以大大加快模式串的移动距离,不是简单的++j,而是j+=max (shift(好后缀), shift(坏字符))
shift(坏字符)分为两种情况:
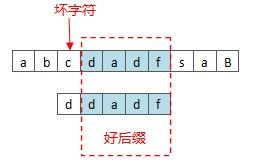
先设计一个数组bmBc['e'],表示坏字符‘e’在模式串中最后一次出现的位置距离模式串末尾的最大长度(如果不出现,则PLen)
- 坏字符没出现在模式串中,这时可以把模式串移动到坏字符的下一个字符,继续比较,如下图:
Case 1:坏字符不出现在模式串中
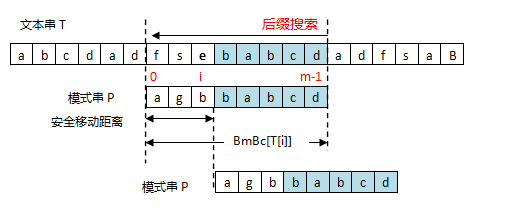
安全移动距离=shift(坏字符)=BmBc[T[i]]-(m-i-1)
安全移动距离=shift(坏字符)=BmBc[T[i]]-(m-i-1)
数组bmBc的创建有两点技巧:若字符不在模式串中,则=strlen(pattern),若在模式串中,则=strlen(pattern)-i-1
//求坏字符数组,某一坏字符距离末尾的长度,若某一字符出现多次,取最右边的,例ababab,则BmBc[a]=1,BmBc[b]=0
void preBmBc(const char *pPattern, int nLen, int BmBc[])
{
for (int i = 0; i < 256; ++i)//char可以用1个字节保存(256)
{
BmBc[i] = nLen;//初始化为nLen,如果坏字符不在模式串中,那么BmBc[i]=nLen,安全移动距离=nPLen-GoodSuffix
}
for (int i = 0; i < nLen; ++i)
{
BmBc[pPattern[i]] = nLen-1-i;//如果坏字符出现在模式串中(以最右一个为准),安全移动距离=nLen-1-i-GoodSuffix(有可能为负值,即倒退)
}
}
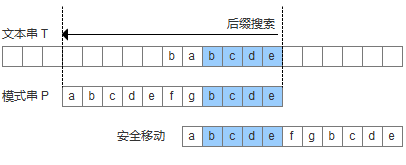
模式串中有多个子串与好后缀完全匹配,选择最左边的子串与好后缀对齐。(case1:完全匹配)
再来看如何根据好后缀规则移动模式串,shift(好后缀)分为三种情况:
- 模式串中有子串匹配上好后缀,此时移动模式串,让该子串和好后缀对齐即可,如果超过一个子串匹配上好后缀,则选择最靠左边的子串对齐。
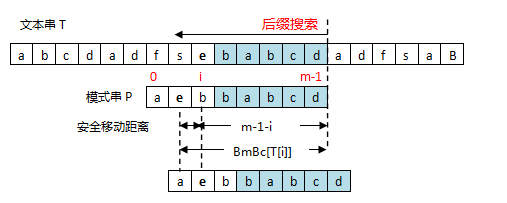
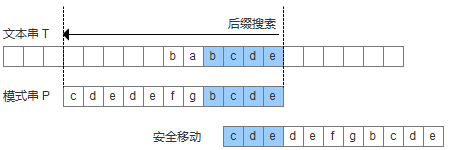
- 模式串中没有子串与好后缀完全匹配(除了下图蓝色部分),则在模式串的开头寻找能与好后缀匹配的最大前缀。(类似KMP的找最大对称串)(case2:部分匹配)
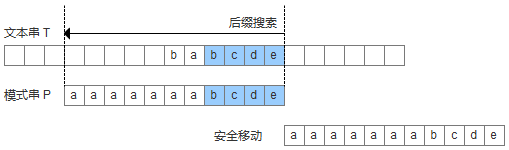
- 模式串中没有子串与好后缀完全匹配,并且在模式串中找不到最长前缀,此时,直接移动模式串到好后缀的下一个字符。
case3:完全不匹配
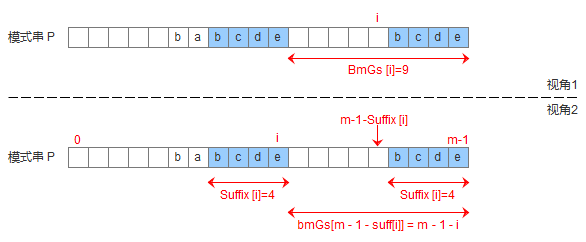
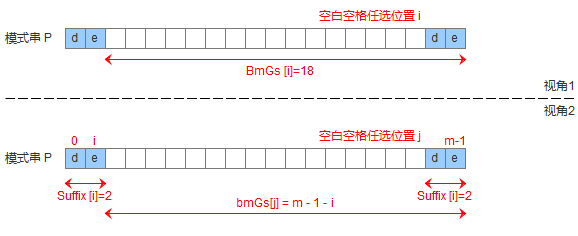
为了实现好后缀规则,需要定义一个数组suffix[],其中suffix[i] = s 表示以i为边界,与模式串后缀匹配的最大长度,
如下图所示,用公式可以描述:满足P[i-s, i] == P[m-s, m]的最大长度s。
构建suffix数组的代码如下:
//寻找好后缀长度
void Suffix(const char *pPattern, int nLen, int *pSuffix)
{
if (0 == nLen)
return;
pSuffix[nLen-1] = 0;//最后一个字符必定为0
for(int i = nLen-2 ; i>=0 ; --i)
{
int suffLen=0 ;//累计后缀长度
while(i-suffLen >=0 && pPattern[i-suffLen] == pPattern[nLen-1-suffLen])
++suffLen;
pSuffix[i]=suffLen;
}
}
模式串中有子串匹配上好后缀有了suffix数组,就可以定义bmGs[]数组,bmGs[i] 表示遇到好后缀时,模式串应该移动的距离,其中i表示好后缀前面一个字符的位置(也就是坏字符的位置),构建bmGs数组分为三种情况,分别对应上述的移动模式串的三种情况
构建bmGs数组的代码如下:
void preBmGs(const char *pPattern, int nLen, int BmGs[])
{
if (0 == nLen)
return ;
//不直接求好后缀数组,因为直接求的话时间复杂度是O(n^2)
//我们先计算出pSuffix数组
int *pSuffix = new int[nLen];
Suffix(pPattern, nLen, pSuffix);
//根据suffix确定好后缀的值,首先全部初始化为nLen
//第三种情况,BmGs[i]=strlen(pattern)
for (int i = 0; i < nLen; ++i)
{
BmGs[i] = nLen;
}
//第一种情况:完全匹配L'(i)
//pSuffix[i]为以i为末尾的好后缀长度
int nMaxPrefix = 0;//累计最大前缀长度
for (int i = 0; i < nLen; ++i)
{
BmGs[nLen-1-pSuffix[i]] = nLen-1-i;
if (pSuffix[i] == i+1)//说明模式串中[0..i]是前缀
{
nMaxPrefix = i+1;
}
}
//第二种情况(最长前缀):部分匹配l'(i) 前缀和后缀的匹配
if (nMaxPrefix > 0)
{
for (int i = nMaxPrefix; i < nLen-1-nMaxPrefix; ++i)
{
if (BmGs[i] == nLen)//填满中间空白空格的值,因为安全移动距离需要缩小
{
BmGs[i] = nLen-nMaxPrefix;//记录的是到末尾的距离
}
}
}
delete []pSuffix;
}
现在BM算法就可以轻易从蛮力法中改进出来:
int BM(const char* pDest, int nDLen, const char* pPattern, int nPLen, int *BmGs, int *BmBc)
{
if (0 == nPLen)//空字符返回-1
return -1;
int nDstart = nPLen-1;
while (nDstart < nDLen)
{
int suffLen = 0;//统计好后缀的长度
while (suffLen < nPLen && pDest[nDstart-suffLen] == pPattern[nPLen-1-suffLen])
++suffLen ;
if (suffLen == nPLen)
{
return nDstart - (nPLen-1);//匹配
}
nDstart += max(BmGs[nPLen-1-suffLen] , BmBc[pDest[nDstart-suffLen]]-suffLen);//安全移动,BmBc可能倒退(负值)
}
return -1;
}
BM算法完整测试代码
#include
#include
using namespace std;
//求坏字符数组,某一坏字符距离末尾的长度,若某一字符出现多次,取最右边的,例ababab,则BmBc[a]=1,BmBc[b]=0
void preBmBc(const char *pPattern, int nLen, int BmBc[])
{
for (int i = 0; i < 256; ++i)//char可以用1个字节保存(256)
{
BmBc[i] = nLen;//初始化为nLen,如果坏字符不在模式串中,那么BmBc[i]=nLen,安全移动距离=nPLen-GoodSuffix
}
for (int i = 0; i < nLen; ++i)
{
BmBc[pPattern[i]] = nLen-1-i;//如果坏字符出现在模式串中(以最右一个为准),安全移动距离=nLen-1-i-GoodSuffix(有可能为负值,即倒退)
}
}
//寻找好后缀长度
void Suffix(const char *pPattern, int nLen, int *pSuffix)
{
if (0 == nLen)
return;
pSuffix[nLen-1] = 0;//最后一个字符必定为0
for(int i = nLen-2 ; i>=0 ; --i)
{
int suffLen=0 ;//累计后缀长度
while(i-suffLen >=0 && pPattern[i-suffLen] == pPattern[nLen-1-suffLen])
++suffLen;
pSuffix[i]=suffLen;
}
}
void preBmGs(const char *pPattern, int nLen, int BmGs[])
{
if (0 == nLen)
return ;
//不直接求好后缀数组,因为直接求的话时间复杂度是O(n^2)
//我们先计算出pSuffix数组
int *pSuffix = new int[nLen];
Suffix(pPattern, nLen, pSuffix);
//根据suffix确定好后缀的值,首先全部初始化为nLen
//第三种情况,BmGs[i]=strlen(pattern)
for (int i = 0; i < nLen; ++i)
{
BmGs[i] = nLen;
}
//第一种情况:完全匹配L'(i)
//pSuffix[i]为以i为末尾的好后缀长度
int nMaxPrefix = 0;//累计最大前缀长度
for (int i = 0; i < nLen; ++i)
{
BmGs[nLen-1-pSuffix[i]] = nLen-1-i;
if (pSuffix[i] == i+1)//说明模式串中[0..i]是前缀
{
nMaxPrefix = i+1;
}
}
//第二种情况(最长前缀):部分匹配l'(i) 前缀和后缀的匹配
if (nMaxPrefix > 0)
{
for (int i = nMaxPrefix; i < nLen-1-nMaxPrefix; ++i)
{
if (BmGs[i] == nLen)//填满中间空白空格的值,因为安全移动距离需要缩小
{
BmGs[i] = nLen-nMaxPrefix;//记录的是到末尾的距离
}
}
}
delete []pSuffix;
}
int BM(const char* pDest, int nDLen, const char* pPattern, int nPLen, int *BmGs, int *BmBc)
{
if (0 == nPLen)//空字符返回-1
return -1;
int nDstart = nPLen-1;
while (nDstart < nDLen)
{
int suffLen = 0;//统计好后缀的长度
while (suffLen < nPLen && pDest[nDstart-suffLen] == pPattern[nPLen-1-suffLen])
++suffLen ;
if (suffLen == nPLen)
{
return nDstart - (nPLen-1);//匹配
}
nDstart += max(BmGs[nPLen-1-suffLen] , BmBc[pDest[nDstart-suffLen]]-suffLen);//安全移动,BmBc可能倒退(负值)
}
return -1;
}
void TestBM()
{
int nFind;
int BmGs[100] = {0};
int BmBc[256] = {0};
// 1 2 3 4
//0123456789012345678901234567890123456789012345678901234
const char dest[] = "Hello , My name is LinRaise,welcome to my blog";
const char pattern[][20] = {
"H",
"He",
"Hel",
"My",
"name",
"wel",
"blog",
"Lin",
"Raise",
"to",
"x",
"y",
"My name",
"to my",
};
int seco=0;
for(int i=0;i
再引用另一篇博文:打破思维之BM算法以供参考.考虑模式串匹配不上母串的最坏情况,后缀蛮力匹配算法的时间复杂度最差是O(n×m),最好是O(n),其中n为母串的长度,m为模式串的长度。BM算法时间复杂度最好是O(n/(m+1)),最差是多少?留给读者思考。
参考资料:
上面的做画图示:图示
柔性字符匹配:点击打开链接