splay 太难了!
我直接懵逼,但是,
我不是会被轻易打倒的,*这题这么难的吗,看题解看题解
不过我偶然遇到了替罪羊树,发现可以谔谔一下。
替罪羊树也(怎么是“也”呢?其实比较的暴力数据结构还是挺多的,比如莫队)是一种优雅的暴力,但是,
在大多情况下珂以踩正解!
暴力碾标算不是梦啊。
替罪羊树的核心思想是:
将不平衡的子树拍扁然后重构。
这样,查找的次数大大减少。
那么如何判断是否不平衡呢?
我们给平衡一个定义:
一棵树的左子树或右子树的节点过多,就是不平衡的。
那如何判断节点多呢?
我们记录a[k].size 为节点 \(k\) 的节点总数,a[k].sh 为剩下的节点总数,尝试玄学一些:
定义一个 \(\alpha\) 为平衡权值(一般取 \(\alpha\in[0.7,0.8]\)),那么当 \(\max\{\text{左儿子的节点数},\text{右儿子的节点数}\}>\alpha×\text{总节点数}\)时,就判断为失衡。
当然还有一种情况比较难想,这里提出来,可以当结论记住。
当该子树被删除的节点过多时,在下面的搜索中会浪费时间,对于是否失衡的判断也会受到一些影响,所以借助拍扁全部删掉删除。
当然如果这个节点不存在直接跳过就好了。
我们可以模拟一下判断是否需要失衡重构的过程:
bool judge(int k)
{
return (a[k].wn&&(alpha*(double)a[k].size<(double)max(a[a[k].ls].size,a[a[k].rs].size)||(double)a[k].sh有点长啊。
那么,如何重构呢?
前面有提到,核心是拍扁:
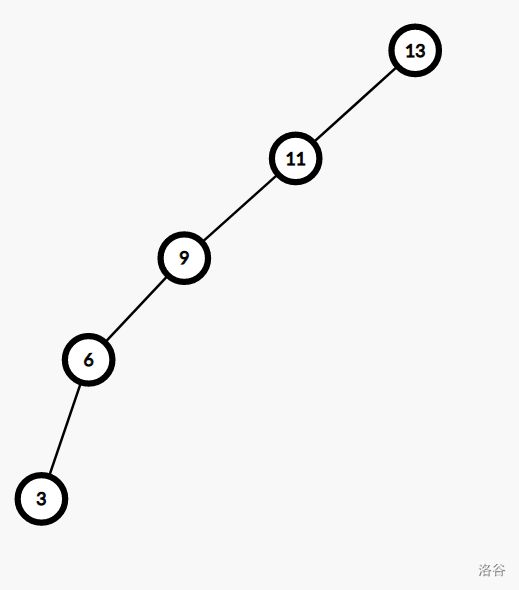
比如有这样一棵二叉查找树:
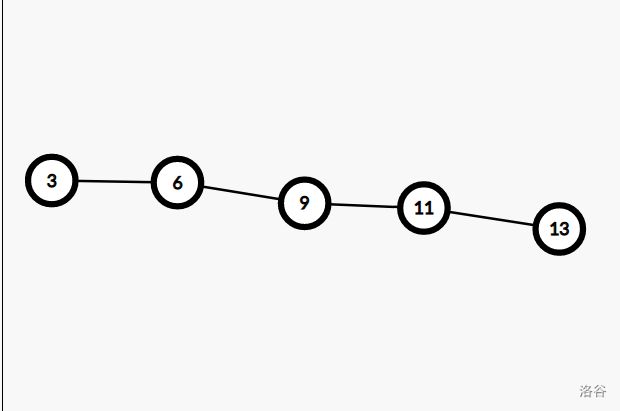
显然十分不平衡,我们用前序遍历(左儿子,根,右儿子)的方式压成数组(直链):
void unfold(int k)
{
if(!k) return;
unfold(a[k].ls);
if(a[k].wn) rt[++crt]=k;
unfold(a[k].rs);
return;
}
最后的 rt[] 数组存的就是前序遍历的点的编号。
其中 a[k].wn 代表 \(k\) 节点上有几个点(也就是说有几个点和 \(k\) 点权值相同),你会发现这样也把没有存在的节点直接踢掉了。
然后我们用中续遍历把他展成一棵树:

具体方法有点像线段树啊:
int rebuild(int l,int r)//返回根的编号
{
if(l>=r) return 0;
int mid=(l+r)>>1;
a[rt[mid]].ls=rebuild(l,mid);
a[rt[mid]].rs=rebuild(mid+1,r);
update(rt[mid]);
return rt[mid];
}
那怎么update呢?
我们发现只需要处理总的节点数和剩下的节点数。
其他的除了只与自身相关的变量就已经更新或根本不用更新。
简单来说就是这样的:
void update(int k)
{
a[k].size=a[a[k].ls].size+a[a[k].rs].size+a[k].wn;
a[k].sh=a[a[k].ls].sh+a[a[k].rs].sh+a[k].wn;
return;
}
总的维护平衡的操作也就是这这样了:
void bal(int& k){crt=0,unfold(k),k=rebuild(1,crt+1);}
我们发现,这不就是 \(dfs\) 吗?
确实,不过为什么能保证复杂度呢?
其实前面已经提到过,在修改很多次后才会失衡。
其实,只需要这样的无脑爆搜操作就可以与什么难以理解的“双旋”媲美了。
如果你理解了,那么你只需要会一般二叉搜索树操作就好了。
不过可能很多人(?)直接跳过了,所以不讲是不可能的。
我们来看例题吧:P3369 【模板】普通平衡树
\(ps:\)下面指的“根”绝大部分都是正搜到的子树的根,要变通。
第一个操作:插入节点。
由于二叉搜索树的性质:左儿子 \(<\) 根 \(<\) 右儿子,直接搜索即可。
分类讨论:
\(1.\) 存在与这个数一样的节点,直接加一下出现次数不断向上更新即可。
\(2.\)不存在和这个数一样的节点。
那怎么办呢?
我们在符合条件(即二叉搜索数性质)的位置插入一个节点即可。
由于我们要修改找到最后一个点的左儿子或右儿子,需要在函数取地址,否则会死。
代码中 a[k].val 代表 \(k\) 点的权值,a[k].wn 为 \(k\) 节点出现的次数,cnt是存在或存在过的节点总数,可以当编号来使唤。
void insert(int& k,int x)
{
if(!k)//由于不存在的儿子为0,这是情况二
{
k=++cnt;
if(!root) root=1;//如果还没有根,那么就把他设成根
//这样便于以下操作从根开始往下搜
a[k].val=x,a[k].ls=a[k].rs=0;
a[k].wn=a[k].size=a[k].sh=1;
}
else
{
if(a[k].val==x) a[k].wn++;//情况一
//按二叉搜索树性质向下找
else if(x你又会问了:
这样失衡次数如果很多不会垮吗?
答案是否定的,因为只插入一个节点不可能次次改变树的平衡度。
这个问题说了三遍了......
操作二:删除节点。
理论上的套路与插入节点异曲同工。
这里只需要处理更新剩下的节点数和节点自身次数,由于操作很少,所以被称为“惰性删除”。
先看代码:
void del(int& k,int x)
{
//if(!k) return;
a[k].sh--;
if(a[k].val==x) a[k].wn--;//可以判断a[k].wn>0?
else
{
if(a[k].val>x) del(a[k].ls,x);
else del(a[k].rs,x);
}
update(k);
if(judge(k)) bal(k);
}
这是保证合法的操作,判断不合法的已被注释。
很简单吧?
下面先不看操作三。
操作(询问?)四:查询第 \(k\) 大。
和权值线段树类似,如果左儿子不够用就在右边,如果够用就在左边。
还有一种比较特殊的情况,如果这个排名正好是根呢?
也就是这种情况:
x>a[a[k].ls].sh&&a[a[k].ls].sh+a[k].wn>=x
注意等号的取与否。
就是无脑模拟一下了:
int at(int k,int x)
{
if(a[k].ls==a[k].rs) return a[k].val;
if(x<=a[a[k].ls].sh) return at(a[k].ls,x);
else if(x>a[a[k].ls].sh&&a[a[k].ls].sh+a[k].wn>=x) return a[k].val;
else return at(a[k].rs,x-a[a[k].ls].sh-a[k].wn);
}
注意用的是剩下的,即 a[k].sh 而非 a[k].size。
下面考虑操作(询问?)三:查询一个数的排名。
我们考虑找到比 \(x\) 小的数的个数 \(+1\) 即可。
我们这里有一个二叉搜索树(假设每个点只出现 \(1\) 次):
假设我们要查找比 \(13\) 小的有几个数。
那么就有这样的回溯路径:
我们注意在空节点处返回 \(0\)(显而易见)。
然后其他的情况分类即可:
\(1.\) 查找的值小于该节点的值,那么就返回他在左子树中的排名。
\(2.\) 查找的值等于该节点的值,那么就返回左子树剩余节点的个数。
\(3.\) 查找的值等于该节点的值,那么返回左子树剩余节点数,该节点出现次数与这个数在右子树的排名的和。
代码实现:
int rkdown(int k,int x)
{
if(!k) return 0;
if(a[k].wn&&a[k].val==x) return a[a[k].ls].sh;
else if(x下面是操作五:询问一个数的前驱。
就是他前面那个数的值,也就是排名为比他小的数的个数的数。
也就是:
at(root,rkdown(root,x))
操作六(询问一个数的后继)怎么办呢?
我们珂以得出这个数最后的排名(指并列时的最后一个的排名),就是这样的:
int rkup(int k,int x)
{
if(!k) return 0;
if(a[k].wn&&x==a[k].val) return a[k].wn+a[a[k].ls].sh;
else if(x你发现只有一个地方,就是当查找的值等于该节点的值时,要把他自身出现的次数算上。
查询后继只需:
at(root,rkup(root,x)+1)
可能 \(+1\) 容易忘,在函数中加上即可:
int rkup(int k,int x)
{
if(!k) return 1;
if(a[k].wn&&x==a[k].val) return 1+a[k].wn+a[a[k].ls].sh;
else if(x这样能保证只加了一个 \(1\),想想为什么。
太简单了,因为搜到底或者正好碰到只可能出现一次。(看什么,自己分析)
那么回答询问时:
at(root,rkup(root,x))
这样,所有的替罪羊树相关知识就讲完了。
是不是豁然开朗呢?细细理解,发现这个东西太好理解了,我的 ds 生涯有救啦。
为了方便 debug ,给出 \(AC\) 代码(全篇):
#include"iostream"
#include"cstdio"
#include"cmath"
#include"cstring"
using namespace std;
#define read(x) scanf("%d",&x)
#define MAXN 100005
const double alpha=0.75;//这个值随心就好了
int n;
int t,x;
struct node
{
int ls,rs;
int size,sh;
int val;
int wn;
node()
{
ls=rs=0;
size=sh=0;
val=0;
wn=0;
}
}a[MAXN];
int root=0;
int rt[MAXN],crt=0;
int cnt=0;
bool judge(int k){return (a[k].wn&&(alpha*(double)a[k].size<(double)max(a[a[k].ls].size,a[a[k].rs].size)||(double)a[k].sh=r) return 0;
int mid=(l+r)>>1;
a[rt[mid]].ls=rebuild(l,mid);
a[rt[mid]].rs=rebuild(mid+1,r);
update(rt[mid]);
return rt[mid];
}
void bal(int& k){crt=0,unfold(k),k=rebuild(1,crt+1);}
void insert(int& k,int x)
{
if(!k)
{
k=++cnt;
if(!root) root=1;
a[k].val=x,a[k].ls=a[k].rs=0;
a[k].wn=a[k].size=a[k].sh=1;
}
else
{
if(a[k].val==x) a[k].wn++;
else if(xx) del(a[k].ls,x);
else del(a[k].rs,x);
}
update(k);
if(judge(k)) bal(k);
}
int rkup(int k,int x)
{
if(!k) return 1;
if(a[k].wn&&x==a[k].val) return 1+a[k].wn+a[a[k].ls].sh;
else if(xa[a[k].ls].sh&&a[a[k].ls].sh+a[k].wn>=x) return a[k].val;
else return at(a[k].rs,x-a[a[k].ls].sh-a[k].wn);
}
int main()
{
read(n);
while(n--)
{
read(t),read(x);
if(t==1) insert(root,x);
else if(t==2) del(root,x);
else if(t==3) printf("%d\n",rkdown(root,x)+1);
else if(t==4) printf("%d\n",at(root,x));
else if(t==5) printf("%d\n",at(root,rkdown(root,x)));
else printf("%d\n",at(root,rkup(root,x)));
}
return 0;
}
那么替罪羊树的时间复杂度是多少呢?
在最坏情况的均摊复杂度是下是 \(\mathcal O(m\log n)\),是十分优秀的算法,这就是“暴力碾标算”的由来。
讲的够详细了吧......
行,点赞吧(<--不要脸)。