LearnGL - 06.2 - Matrix - 矩阵03
文章目录
- 逆矩阵-inverse matrix
- 行列式-determinant
- 伴随矩阵-adjugate、adjoint matrix
- 余子式-Cofactor、Minor
- 余子项
- 余子式
- 代数余子式-Algebraic cofactor、Minor
- 伴随矩阵-二维的例子
- 总结 & 练习
- References
LearnGL - 学习笔记目录
本人才疏学浅,如有什么错误,望不吝指出。
上些篇:
- LearnGL - 06 - Matrix - 矩阵01,了解了矩阵就是定义一个坐标空间的轴向
- LearnGL - 06.1 - Matrix - 矩阵02,了解了一些矩阵的乘法的维度限制
这一篇:了解 行列式(determinant)、逆矩阵(inverse)、伴随矩阵(adjugate、adjoint)、余子式(cofactor、minor)、代数余子式(algebraic cofactor、minor)。
逆矩阵-inverse matrix
在计算机3D图形学中,在实现一些特殊功能的时候,特别是一些坐标还原,或重构成其他坐标时,都可能会用到逆矩阵。
一个变换矩阵可以将我们传入的向量(组)变换到此变换矩阵中的另一个坐标系中,如果我们要撤销这些变换呢,那么就需要逆过来变换,这个逆变换的矩阵,就叫:逆矩阵。
我们都知道,标量乘以标量,如: 1 × n = n 1 \times n = n 1×n=n,就是1乘以任意数,等于那个数的本身。
同样在矩阵中也有类型的,如: I ⋅ M = M I\cdot M=M I⋅M=M, I I I是单位矩阵(左上角到右下角都是1,其余都是0的方阵)乘以任意矩阵都等于那个矩阵的本身。
1 × n = n 1 \times n = n 1×n=n,同是 1 n ⋅ n = 1 \frac{1}{n}\cdot n=1 n1⋅n=1,而这个 1 n \frac{1}{n} n1就是n的倒数。
同样的也有: M − 1 ⋅ M = M ⋅ M − 1 = I M^{-1}\cdot M=M \cdot M^{-1}=I M−1⋅M=M⋅M−1=I,而这其中的 M − 1 M^{-1} M−1就是 M M M的逆矩阵。
在求逆矩阵时,需要用到行列式的功能。
行列式-determinant
先来讲一下,determinant - 矩阵行列式(这里我觉得中文翻译的理解不好),为啥要一个“式”字结尾,感觉会误导很多人,可以参考这篇文章的讲解:行列式determinant到底是个啥?,其实 determinant 就是求一个矩阵的N个轴(N个列向量,N>0,范围:1,2,…,n)围起来的空间大小(一维)、面积(二维)、体积(三维)、无法描述的变换空间大小(大于三维),最终的值是一个标量,注意:行列式结果是一个标量,并不是什么式子、也不是向量。
所以可以理解,它就是表述一个变换的基的包围空间的大小。
变换:
- 一维中,假设一个2,就是可以把某个东西可以变大2倍的变换数值,它的determinant就是2,长度。
- 二维中,假设 x → ( 0.5 , 0 ) y → ( 0 , 2 ) \overrightarrow x(0.5,0) \overrightarrow y(0,2) x(0.5,0)y(0,2),就是可以让一个存在于二维下的数值对象(a,b)可以让它在 x → ( 0.5 , 0 ) y → ( 0 , 2 ) \overrightarrow x(0.5,0) \overrightarrow y(0,2) x(0.5,0)y(0,2) 的变换后的结果: [ x → y → ∣ ∣ ] ⋅ ( a b ) → [ 0.5 0 0 2 ] ⋅ ( a b ) = ( 0.5 ⋅ a 2 ⋅ b ) \begin{bmatrix} \overrightarrow x & \overrightarrow y\\ |&| \end{bmatrix} \cdot \left(\begin{matrix}a\\b\end{matrix}\right) \rightarrow \begin{bmatrix} 0.5 & 0 \\ 0 & 2 \end{bmatrix} \cdot \left(\begin{matrix}a\\b\end{matrix}\right) = \left(\begin{matrix}0.5\cdot a\\2\cdot b\end{matrix}\right) [x∣y∣]⋅(ab)→[0.5002]⋅(ab)=(0.5⋅a2⋅b),相当于把a缩小一倍,b放大一倍。它的determinant就是0.5*2=1面积。
- 同理三维中的是体积。
但上面都是比较理想的变换矩阵,就是他们的每列向量之间都是垂直的(正交的)所以求他们围起来空间,直接向量它们的向量长度就可以了。
但是如果他们不是垂直的(正交的),这个时候就需要将每个轴之间x,y,z分量上有参差的量围成的空间给减去,才能得到最终的空间。
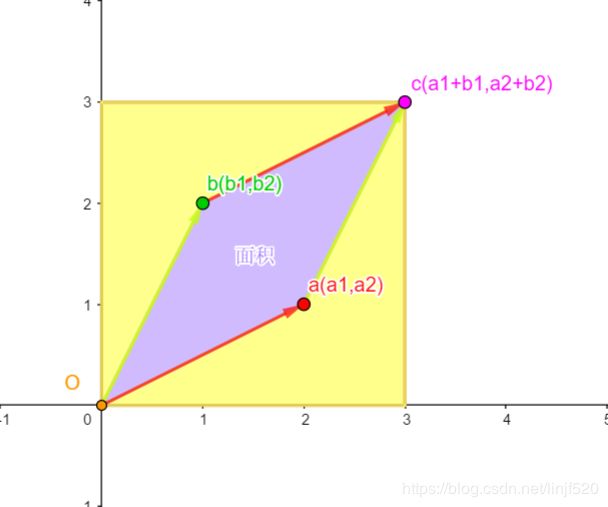
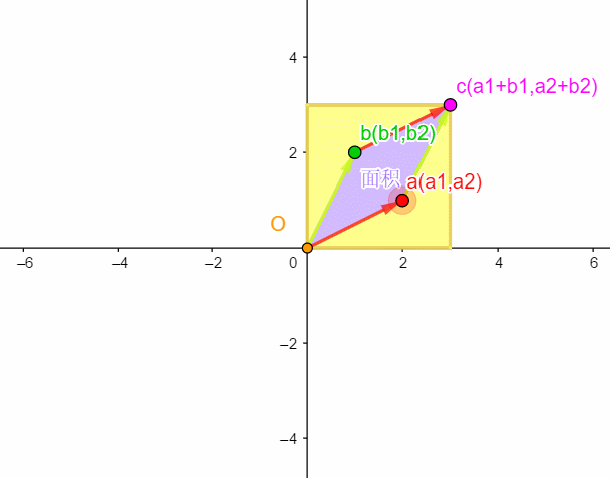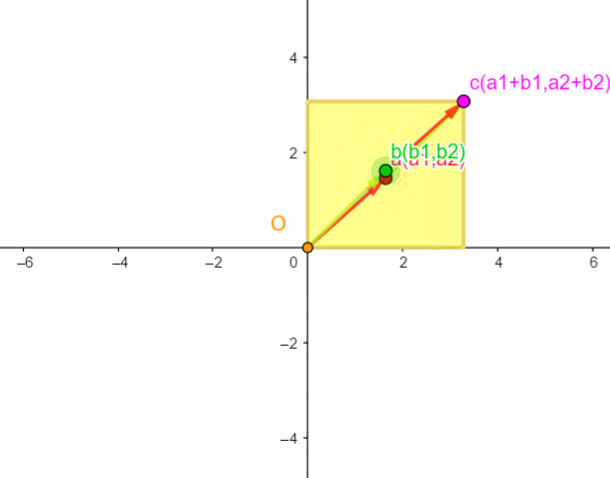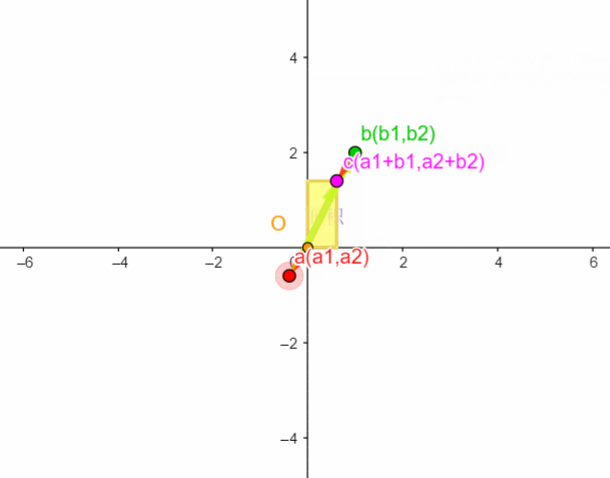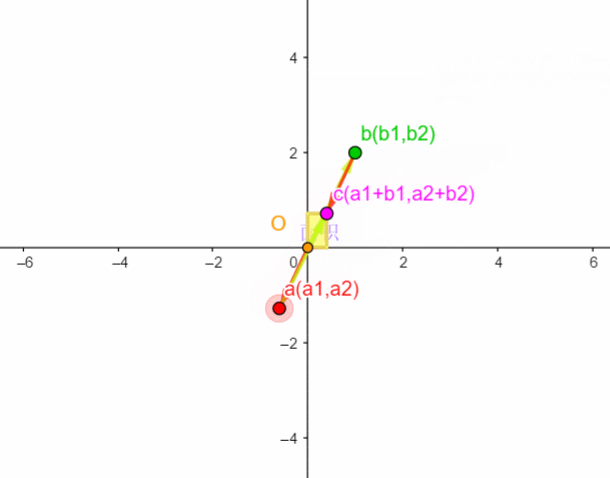
如上图,a(a1,a2),b(b1,b2)向量就是不互相垂直的,黄色就是a(a1,a2)与b(b1,b2)向量x,y分量上参差的分量围起来的面积,着黄色部分的面积就是整个长方形需要减去的面积,最终得到的面积就是a,b向量围起来的平行四边形的面积。
也可以从百度百科中的:矩阵行列式的公式: d e t ( a b c d ) = a d − b c det\left(\begin{matrix} a & b \\ c & d \end{matrix}\right) =ad-bc det(acbd)=ad−bc 来发现一些线索。
如果b,c为零呢? d e t ( a b c d ) = a d − b c → d e t ( a 0 0 d ) = a d − 0 = a d det\left(\begin{matrix} a & \color{#ff0000}b \\ \color{#ff0000}c & d \end{matrix}\right) =ad-{\color{#ff0000}bc}\rightarrow det\left(\begin{matrix} a & \color{#ff0000}0 \\ \color{#ff0000}0 & d \end{matrix}\right) =ad-{\color{#ff0000}0}=ad det(acbd)=ad−bc→det(a00d)=ad−0=ad,那就是向量(a,0)与向量(0,d)垂直了,前者平行于x轴,后者平行于y轴,这时面积就等于ad了,如下图
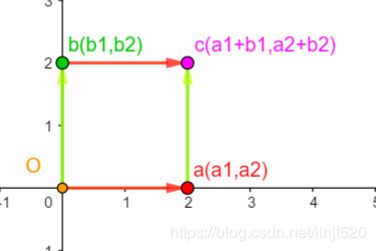
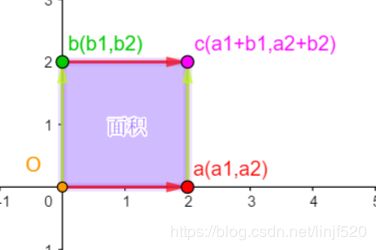
所以 行列式就是求变换矩阵的轴包围的一个空间大小,只不过在这个二维空间单位是面积,三维就是体积了,一维就是长度。
假设有矩阵A: [ a b c d ] \begin{bmatrix} a & b\\ c & d \end{bmatrix} [acbd]
det(A),或是矩阵A的行列式 又或是记作 ∣ A ∣ |A| ∣A∣,那么: d e t ( A ) = ∣ A ∣ = a d − b c det(A)=|A|=ad-bc det(A)=∣A∣=ad−bc
那么矩阵A的逆矩阵,记作 A − 1 A^{-1} A−1,那么 A − 1 = 1 ∣ A ∣ ⋅ [ d − b − c a ] = 1 a d − b c ⋅ [ d − b − c a ] A^{-1}=\frac{1}{|A|}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix}=\frac{1}{ad-bc}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} A−1=∣A∣1⋅[d−c−ba]=ad−bc1⋅[d−c−ba]
暂且我们不管这个矩阵 [ d − b − c a ] \begin{bmatrix}d & -b \\ -c & a\end{bmatrix} [d−c−ba]是怎么来的,它看起来就像是a与d交换,b,c添加负数了。这个矩阵叫作:伴随矩阵。后面再详细的搬运一波内容。
这个是2X2矩阵的逆矩阵,我们可以验证一下:
那么继续逆矩阵的内容
有一个矩阵A:
A = [ a b c d ] = [ 8 − 2 4 6 ] A=\begin{bmatrix}a & b \\ c & d\end{bmatrix}=\begin{bmatrix}8 & -2 \\ 4 & 6\end{bmatrix} A=[acbd]=[84−26]
A的逆矩阵为:
A − 1 = 1 a d − b c ⋅ [ d − b − c a ] A^{-1}=\frac{1}{ad-bc}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} A−1=ad−bc1⋅[d−c−ba]
A − 1 = 1 8 ⋅ 6 − ( − 2 ) ⋅ 4 ⋅ [ 6 − ( − 2 ) − 4 8 ] A^{-1}=\frac{1}{8\cdot 6-(-2)\cdot 4}\cdot\begin{bmatrix}6 & -(-2) \\ -4 & 8\end{bmatrix} A−1=8⋅6−(−2)⋅41⋅[6−4−(−2)8]
A − 1 = 1 48 + 8 ⋅ [ 6 2 − 4 8 ] A^{-1}=\frac{1}{48+8}\cdot\begin{bmatrix}6 & 2 \\ -4 & 8\end{bmatrix} A−1=48+81⋅[6−428]
A − 1 = 1 56 ⋅ [ 6 2 − 4 8 ] A^{-1}=\frac{1}{56}\cdot\begin{bmatrix}6 & 2 \\ -4 & 8\end{bmatrix} A−1=561⋅[6−428]
A − 1 = [ 6 ⋅ 1 56 2 ⋅ 1 56 − 4 ⋅ 1 56 8 ⋅ 1 56 ] A^{-1}=\begin{bmatrix}6\cdot \frac{1}{56} & 2 \cdot \frac{1}{56} \\ -4 \cdot \frac{1}{56} & 8 \cdot \frac{1}{56}\end{bmatrix} A−1=[6⋅561−4⋅5612⋅5618⋅561]
A − 1 = [ 6 56 2 56 − 4 56 8 56 ] A^{-1}=\begin{bmatrix}\frac{6}{56} & \frac{2}{56} \\ -\frac{4}{56} & \frac{8}{56}\end{bmatrix} A−1=[566−564562568]
OK,现在计算得 A − 1 = [ 6 56 2 56 − 4 56 8 56 ] A^{-1}=\begin{bmatrix}\frac{6}{56} & \frac{2}{56} \\ -\frac{4}{56} & \frac{8}{56}\end{bmatrix} A−1=[566−564562568],然将与 A = [ 8 − 2 4 6 ] A=\begin{bmatrix}8 & -2 \\ 4 & 6\end{bmatrix} A=[84−26]相乘,结果看看是否等于 I I I:
A − 1 ⋅ A = I A^{-1}\cdot A = I A−1⋅A=I
[ 6 56 2 56 − 4 56 8 56 ] ⋅ [ 8 − 2 4 6 ] = [ 1 0 0 1 ] \begin{bmatrix}\frac{6}{56} & \frac{2}{56} \\ -\frac{4}{56} & \frac{8}{56}\end{bmatrix} \cdot \begin{bmatrix}8 & -2 \\ 4 & 6\end{bmatrix}=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} [566−564562568]⋅[84−26]=[1001]
[ 6 ⋅ 8 56 + 2 ⋅ 4 56 6 ⋅ ( − 2 ) 56 + 2 ⋅ 6 56 − 4 ⋅ 8 56 + 8 ⋅ 4 56 − 4 ⋅ ( − 2 ) 56 + 8 ⋅ 6 56 ] = [ 1 0 0 1 ] \begin{bmatrix}\frac{6 \cdot 8}{56} + \frac{2 \cdot 4}{56} & \frac{6 \cdot (-2)}{56} + \frac{2 \cdot 6}{56} \\ -\frac{4\cdot 8}{56} + \frac{8\cdot 4}{56} & -\frac{4\cdot (-2)}{56} + \frac{8 \cdot 6}{56}\end{bmatrix} =\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} [566⋅8+562⋅4−564⋅8+568⋅4566⋅(−2)+562⋅6−564⋅(−2)+568⋅6]=[1001]
[ 48 56 + 8 56 − 12 56 + 12 56 − 32 56 + 32 56 8 56 + 48 56 ] = [ 1 0 0 1 ] \begin{bmatrix}\frac{48}{56} + \frac{8}{56} & \frac{-12}{56} + \frac{12}{56} \\ -\frac{32}{56} + \frac{32}{56} & \frac{8}{56} + \frac{48}{56}\end{bmatrix} =\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} [5648+568−5632+563256−12+5612568+5648]=[1001]
[ 56 56 0 0 56 56 ] = [ 1 0 0 1 ] \begin{bmatrix}\frac{56}{56} & 0 \\ 0 & \frac{56}{56}\end{bmatrix} =\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} [5656005656]=[1001]
[ 1 0 0 1 ] = [ 1 0 0 1 ] \begin{bmatrix}1& 0 \\ 0 & 1\end{bmatrix} =\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} [1001]=[1001]
OK,计算完毕。反过来的: A ⋅ A − 1 = I A\cdot A^{-1} = I A⋅A−1=I也是一样的。
还有另一个中计算:Matrix Inverse – 逆矩阵,这种方式可视化是以行向量来分析求解的。
而我们上面使用的是列,建议使用列的方式,更加贴合各种软件中计算。
矩阵的逆矩阵不一定存在,由几种方式可以判断来,先看看二维的逆矩阵的公式:
A − 1 = 1 ∣ A ∣ ⋅ [ d − b − c a ] = 1 a d − b c ⋅ [ d − b − c a ] A^{-1}=\frac{1}{|A|}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix}=\frac{1}{ad-bc}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} A−1=∣A∣1⋅[d−c−ba]=ad−bc1⋅[d−c−ba]
此公式中: d e t ( A ) = ∣ A ∣ = a d − b c det(A)=|A|=ad-bc det(A)=∣A∣=ad−bc
如果 ∣ A ∣ = 0 |A|=0 ∣A∣=0,那么这个式子就 A − 1 A^{-1} A−1的公式中会有除以 0 0 0而无意义。
因为 ∣ A ∣ = a d − b c = 0 |A|=ad-bc=0 ∣A∣=ad−bc=0,所以 A − 1 A^{-1} A−1矩阵有无意义,会是否存在,取决于 A A A矩阵列向量的值。
如果细心观察,可以看出: A = [ a b c d ] A=\begin{bmatrix}a & b\\c & d\end{bmatrix} A=[acbd],矩阵 A A A的第一列向量是: [ a c ] \begin{bmatrix}a\\c\end{bmatrix} [ac],第二列向量是: [ b d ] \begin{bmatrix}b\\d\end{bmatrix} [bd],而 ∣ A ∣ = a d − b c |A|=ad-bc ∣A∣=ad−bc,其实就是:两列向量的叉乘: [ a c ] × [ b d ] = a d − b c \begin{bmatrix}a\\c\end{bmatrix} \times \begin{bmatrix}b\\d\end{bmatrix}=ad-bc [ac]×[bd]=ad−bc。
两个非零向量叉乘的结果为0的时候就只有这两个向量是:相同方向,或是相反方向的,即:两向量共线。
所以如果一个二维变换矩阵的列向量如果向量是共线的,那么该矩阵就没有逆矩阵。
而按行列式,或是determinant的理解就是:如果一个二维变换矩阵的行列式为0,就是变换矩阵的基围起来的空间大小为0(这里的大小至少是面积、体积,或以上),那么此变换矩阵没有逆矩阵。
所以在判断二维矩阵的逆矩阵是否存在,可以根据以下几种方式:
- 用式子来总结: A − 1 = 1 ∣ A ∣ ⋅ [ d − b − c a ] A^{-1}=\frac{1}{|A|}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} A−1=∣A∣1⋅[d−c−ba],当 ∣ A ∣ = 0 |A|=0 ∣A∣=0,则 A − 1 A^{-1} A−1无意义,则 A A A的逆矩阵 A − 1 A^{-1} A−1不存在。
- 而: ∣ A ∣ = 0 |A|=0 ∣A∣=0,也代表: a d − b c = 0 ad-bc=0 ad−bc=0,也代表: a d = b c ad=bc ad=bc,也代表: a b = c d \frac{a}{b}=\frac{c}{d} ba=dc,则 A A A不存在逆矩阵。
- 而: a b = c d \frac{a}{b}=\frac{c}{d} ba=dc,也可以看成是: k = a b = c d k=\frac{a}{b}=\frac{c}{d} k=ba=dc,类似直线斜率的方式,就像 Matrix Inverse – 逆矩阵 中最后是以 [ a b c d ] \begin{bmatrix}\color{#ff0000}a & \color{#ff0000}b \\ \color{#00ff00}c & \color{#00ff00}d\end{bmatrix} [acbd]中的量行的数值分别当作是直线的斜率: a b = c d {\color{#ff0000}\frac{a}{b}}={\color{#00ff00}\frac{c}{d}} ba=dc,则 A A A也不存在逆矩阵。
- 而: a d = b c ad=bc ad=bc,除了可以推导出: k = a b = c d k=\frac{a}{b}=\frac{c}{d} k=ba=dc,也一样可以按: a c = c b \frac{a}{c}=\frac{c}{b} ca=bc来判断,这样就是列向量当作直线,并比较它们两的斜率。
上面的直线斜率的方式,可以以这种方式来看待矩阵,就像是直线方程组,把矩阵的元素当作是方程组中的系数:
[ a b c d ] ⋅ [ x y ] = [ e f ] \begin{bmatrix} a & b\\ c & d \end{bmatrix} \cdot \begin{bmatrix} x\\ y \end{bmatrix} =\begin{bmatrix} e\\ f \end{bmatrix} [acbd]⋅[xy]=[ef]
它其实就是:
[ a c ] ⋅ x + [ b d ] ⋅ y = [ e f ] \begin{bmatrix} a \\ c \end{bmatrix} \cdot x + \begin{bmatrix} b \\ d \end{bmatrix} \cdot y =\begin{bmatrix} e\\ f \end{bmatrix} [ac]⋅x+[bd]⋅y=[ef]
写成:
a x + b y = e a x + d y = f ax + by = e\\ ax + dy = f ax+by=eax+dy=f
变形以下:
b y = − a x + e d y = − a x + f by = -ax + e\\ dy = -ax + f by=−ax+edy=−ax+f
再变形:
y = − a b x + e b y = − a d x + f d y = -\frac{a}{b}x + \frac{e}{b}\\ y = -\frac{a}{d}x + \frac{f}{d} y=−bax+bey=−dax+df
OK,在看看,这个与我们的直线方程的: y = k x + b y = kx + b y=kx+b,是否很像?
所以我们可以把: k : − a b = − a d k:-\frac{ a}{b}=-\frac{a}{d} k:−ba=−da,看作是斜率,然后等式两边的符号,就成了: k : a b = a d k:\frac{ a}{b}=\frac{a}{d} k:ba=da
然后是直线的上下位移量: b : e b = f d b:\frac{e}{b}=\frac{f}{d} b:be=df,但是直线方程上的 b b b不影响行列式,因为 b b b只会影响直线之间是重叠共线还是平行。
所以两个直线的斜率 k k k 相等了,就平行或共线了,那么矩阵的行列式就为0,那么也就不存在逆矩阵了。
还可以理解为直线方程组的各项未知数(元)的系数的话,那么说明两直线无x,y的解,此直线方程无根。因为他们是共线(无穷个交点,无穷个解)或平行(一个交点都没有,一个解都没有)了。两条直线方程有解的话,说明有一个x,y点是两条直线的交点。
这类 n n n阶方阵的矩阵如果 不存在 逆矩阵(determinant 或 行列式 为 0),则称为:奇异 矩阵。
矩阵如果 存在 逆矩阵(determinant 或 行列式 不为 0),则称为:非奇异 矩阵。
也可以参考百度百科的:奇异矩阵,奇异矩阵也叫:singular matrix。
可以看到,当矩阵中的两列向量在共线后,四边形的面积就为0了(紫色的区域大小为0),也就是行列式为0,那么这样的矩阵是没有逆矩阵的。
伴随矩阵-adjugate、adjoint matrix
伴随矩阵英文叫:adjugate matrix,也叫 adjoint matrix。
也可参考百度百科中说明:伴随矩阵。
早在之前的其他文章中有表述过,数学是需要很高洞察力的学科,需要去观察它的规律。
然后聪明的人类发明了数学公式符号来表示这些规律,如:斐波那契数列、对数,指数,三角函数,等等,等等,这些都有一些简洁的公式,这里就不一一搬砖了,可自行搜索。
而伴随矩阵也是被这些数学家们发现了它的特性,它的作用,也可以用于计算出逆矩阵而用的。
(这里我猜测是数学家们先计算出了逆矩阵的方法,可能计算过程太过于繁琐,然后提炼到最精简的结果时,发现了这一结果是可以从现有矩阵中的数值来求出来的,但它到底是怎么被发现的,这一历史没有记录,我也搜索不到,但这些过程是非常有参考意义的,我也惊讶于竟然没有记录,如果有记录的话,会对后人可能有更多的理解,或是更多特性的发现)
下面我引用百度百科中的一句:
如果二维矩阵可逆,那么它的逆矩阵和它的伴随矩阵之间只差一个系数,对多维矩阵也存在这个规律。
照搬一下之前的求矩阵 A A A的逆矩阵的公式:
A − 1 = 1 ∣ A ∣ ⋅ [ d − b − c a ] = 1 a d − b c ⋅ [ d − b − c a ] A^{-1}=\frac{1}{|A|}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix}=\frac{1}{ad-bc}\cdot\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} A−1=∣A∣1⋅[d−c−ba]=ad−bc1⋅[d−c−ba]
矩阵 [ d − b − c a ] \begin{bmatrix}d & -b \\ -c & a\end{bmatrix} [d−c−ba] 就是伴随矩阵。
留意上面引用百度百科说的,它(伴随矩阵)与逆矩阵就差一个系数,这个系数就是:determinant的倒数,即:矩阵行列式的倒数: 1 d e t ( A ) = 1 ∣ A ∣ \frac{1}{det(A)}=\frac{1}{|A|} det(A)1=∣A∣1,二维中(或说是二阶方阵) 的这个系数就是: 1 a d − b c \frac{1}{ad-bc} ad−bc1。
就像上面所说的,至于这个伴随矩阵是怎么得来的,之前我只是简单的描述的一下:
“矩阵 [ d − b − c a ] \begin{bmatrix}d & -b \\ -c & a\end{bmatrix} [d−c−ba]是怎么来的,它看起来就像是a与d交换,b,c添加了负数。”
这是我个人观察的规律,但其实它是由一段公式计算出来的,只不过二维矩阵的伴随矩阵比较简单的规律。
但如果要计算N维(或说N阶)矩阵时,还是需要用公式来计算好些,因为大于二维以上的矩阵的伴随矩阵的计算复杂度会越来越大。
说是有一个公式可以算出来的,但伴随矩阵的式子又是怎么来的,我们也不知道,查找的资料中没有收录这方面的信息,它的公式是:
矩阵 A A A的伴随矩阵,记作: A ∗ A^* A∗,它的式子为:
注意: A ∗ A^* A∗的每项元素做了调整从: A 行 列 A_{\red行\green列} A行列位置上的值调整为: A 列 行 A_{\green列\red行} A列行的值(注意下标左边还是表示 行,右边的还是表示 列,上面说的只是他们的转置情况)。可以理解为 伴随矩阵 是 处理了 转置过 的,就是 行和列对调过 的。
A ∗ = [ A 1 1 A 1 2 ⋯ A 1 n A 2 1 A 2 2 ⋯ A 2 n ⋮ ⋮ ⋱ ⋮ A n 1 A n 2 ⋯ A n n ] A^*=\begin{bmatrix} A_{\red 1\green 1} & A_{\red 1\green 2} & \cdots & A_{\red 1\green n} \\ A_{\red 2\green 1} & A_{\red 2\green 2} & \cdots & A_{\red 2\green n} \\ \vdots & \vdots & \ddots & \vdots \\ A_{\red n\green 1} & A_{\red n\green 2} & \cdots & A_{\red n\green n} \end{bmatrix} A∗=⎣⎢⎢⎢⎡A11A21⋮An1A12A22⋮An2⋯⋯⋱⋯A1nA2n⋮Ann⎦⎥⎥⎥⎤
这是错误的,之前没有留意到这个下标不一样,导致我在后续验算是发现结果不对,-_-!!!:
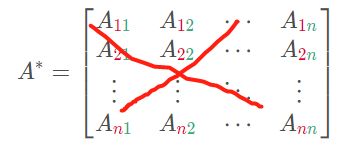
下面的结果是 转置后 的,才是对的:
A ∗ = [ A 1 1 A 2 1 ⋯ A n 1 A 1 2 A 2 2 ⋯ A n 2 ⋮ ⋮ ⋱ ⋮ A 1 n A 2 n ⋯ A n n ] A^*=\begin{bmatrix} A_{\green 1\red 1} & A_{\green 2\red 1} & \cdots & A_{\green n\red 1} \\ A_{\green 1\red 2} & A_{\green 2\red 2} & \cdots & A_{\green n\red 2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{\green 1\red n} & A_{\green 2\red n} & \cdots & A_{\green n\red n} \end{bmatrix} A∗=⎣⎢⎢⎢⎡A11A12⋮A1nA21A22⋮A2n⋯⋯⋱⋯An1An2⋮Ann⎦⎥⎥⎥⎤
矩阵中的元素 A i j A_{ij} Aij是 代数余子式,下面会讲到。
假设有个3x3矩阵 A A A:
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} A=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤
要求伴随矩阵,我们又要先了解下面要讲到:余子式: M i j M_{ij} Mij。后面再加以详细的搬砖。
我们要求得矩阵 A A A的伴随矩阵就等于:它的矩阵 A A A每一项元素的 代数余子式。这里又有一个术语:代数余子式: A i j = ( − 1 ) i + j ⋅ M i j A_{ij}=(-1)^{i+j} \cdot M_{ij} Aij=(−1)i+j⋅Mij(如果要我用一个表情,我会用一个:捂脸哭笑的表情)。
余子式: M i j M_{ij} Mij 与 代数余子式: A i j = ( − 1 ) i + j ⋅ M i j A_{ij}=(-1)^{i+j} \cdot M_{ij} Aij=(−1)i+j⋅Mij 在公式上看的话,后者会多了一个符号的计算: ( − 1 ) i + j (-1)^{i+j} (−1)i+j。后面在加以详细的搬砖。现在先跳过,那么继续伴随矩阵的计算:
所以 A ∗ A^* A∗ 中每一项 代数与字数 也等于 带符号 的 余子式 :
A ∗ = [ A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋱ ⋮ A 1 n A 2 n ⋯ A n n ] = [ ( − 1 ) 1 + 1 ⋅ M 11 ( − 1 ) 2 + 1 ⋅ M 21 ⋯ ( − 1 ) n + 1 ⋅ M n 1 ( − 1 ) 1 + 2 ⋅ M 12 ( − 1 ) 2 + 2 ⋅ M 22 ⋯ ( − 1 ) n + 2 ⋅ M n 2 ⋮ ⋮ ⋱ ⋮ ( − 1 ) 1 + n ⋅ M 1 n ( − 1 ) 2 + n ⋅ M 2 n ⋯ ( − 1 ) n + n ⋅ M n n ] A^*=\begin{bmatrix} A_{11} & A_{21} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{bmatrix}=\begin{bmatrix} (-1)^{1+1}\cdot M_{11} & (-1)^{2+1}\cdot M_{21} & \cdots & (-1)^{n+1}\cdot M_{n1} \\ (-1)^{1+2}\cdot M_{12} & (-1)^{2+2}\cdot M_{22} & \cdots & (-1)^{n+2}\cdot M_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ (-1)^{1+n}\cdot M_{1n} & (-1)^{2+n}\cdot M_{2n} & \cdots & (-1)^{n+n}\cdot M_{nn} \end{bmatrix} A∗=⎣⎢⎢⎢⎡A11A12⋮A1nA21A22⋮A2n⋯⋯⋱⋯An1An2⋮Ann⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡(−1)1+1⋅M11(−1)1+2⋅M12⋮(−1)1+n⋅M1n(−1)2+1⋅M21(−1)2+2⋅M22⋮(−1)2+n⋅M2n⋯⋯⋱⋯(−1)n+1⋅Mn1(−1)n+2⋅Mn2⋮(−1)n+n⋅Mnn⎦⎥⎥⎥⎤
在我们这个3x3矩阵 A A A例子中就是(注意行列 下标 是 转置 过的):
A ∗ = [ A 1 1 A 2 1 A 3 1 A 1 2 A 2 2 A 3 2 A 1 3 A 2 3 A 3 3 ] A^*=\begin{bmatrix} A_{\green 1\red 1} & A_{\green 2\red 1} & A_{\green 3\red 1} \\ A_{\green 1\red 2} & A_{\green 2\red 2} & A_{\green 3\red 2} \\ A_{\green 1\red 3} & A_{\green 2\red 3} & A_{\green 3\red 3} \end{bmatrix} A∗=⎣⎡A11A12A13A21A22A23A31A32A33⎦⎤
余子式-Cofactor、Minor
余子式:英文叫:Cofactor,或:Minor,有辅助因子,或是辅助项,次级项,等意思。
余子式它的符号记作: M i j M_{ij} Mij, i i i和 j j j分别是第 i i i行和第 j j j列的意思, M i j M_{ij} Mij代表的就是减去第 i i i行和第 j j j列后的n-1方阵的行列式。这里先来个简述,后面会重复强调意思。
而中文的理解中在于:“余”字。然后又是令人费解的“式”字。
- 余字:减去对应的的行与列之后剩余的所有项,重组的新的n-1方阵。
- 式字:教你理解这个“式”子的方法,你可以把它理解成编程语言中的:表达式。而编程中的表达式最终会有一个值的,所以式就是表达式,就是会得到一个值的式子。(前面说的 行列式 中的“式”字也是可以这么理解的)
因为它是从原始n方阵中,减去对应的的第 i i i行与第 j j j列之后剩余的所有项,重组的新的n-1方阵的 行列式(注意它是一个余项组成而成的n-1方阵的行列式(determinant),所以它将会是一个值):
还是用回上面的个3x3矩阵 A A A:
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} A=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤
中,假设我要求第2行第1列的余子式,先分两步:
- 先得出 余项,因为是原来的一部分的项目,所以我们叫:余子项
- 再根据 余子项 来求这个 余子项行列式,所以简称 余子式
余子项
第2行第1列的余子项:
先将要删除的第2行第1列的所有项的用红色标出来:
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} \color{#ff0000}a_{11} & a_{12} & a_{13} \\ \color{#ff0000}a_{21} & \color{#ff0000}a_{22} & \color{#ff0000}a_{23} \\ \color{#ff0000}a_{31} & a_{32} & a_{33} \end{bmatrix} A=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤
再将这些项删除:
A = [ 删 除 a 12 a 13 删 除 删 除 删 除 删 除 a 32 a 33 ] A=\begin{bmatrix} \color{#ff0000}删除 & a_{12} & a_{13} \\ \color{#ff0000}删除 & \color{#ff0000}删除 & \color{#ff0000}删除 \\ \color{#ff0000}删除 & a_{32} & a_{33} \end{bmatrix} A=⎣⎡删除删除删除a12删除a32a13删除a33⎦⎤
删除,得到 余子项:
B 21 = [ a 12 a 13 a 32 a 33 ] B_{21}=\begin{bmatrix} a_{12} & a_{13} \\ a_{32} & a_{33} \end{bmatrix} B21=[a12a32a13a33]
余子式
然后是这个用这个 余子项 来来计算矩阵 B B B 的 行列式(determinant):
那么 余子式 记作 M i j M_{ij} Mij,我们的 i i i是2, j j j是1:
M 21 = d e t ( B 21 ) = [ a 12 a 13 a 32 a 33 ] = a 12 ⋅ a 33 − a 13 ⋅ a 32 M_{21}=det(B_{21})=\begin{bmatrix} \color{#ff0000}a_{12} & \color{#00aa00}a_{13} \\ \color{#00aa00}a_{32} & \color{#ff0000}a_{33} \end{bmatrix} ={\color{#ff0000}a_{12}\cdot a_{33}} - {\color{#00aa00}a_{13} \cdot a_{32}} M21=det(B21)=[a12a32a13a33]=a12⋅a33−a13⋅a32
然后是:其他的 M i j M_{ij} Mij都可以使用这种方法计算出对应3x3矩阵中的每一项元素的余子式。
代数余子式-Algebraic cofactor、Minor
我们前面说了伴随矩阵就是每一项的 代数余子式。
而 余子式 与 代数余子式 的区别前面也说过,这里再重新强调一下:
余子式: M i j M_{ij} Mij 与 代数余子式: A i j = ( − 1 ) i + j ⋅ M i j A_{ij}=(-1)^{i+j} \cdot M_{ij} Aij=(−1)i+j⋅Mij 在公式上看的话,后者会多了一个符号的计算: ( − 1 ) i + j (-1)^{i+j} (−1)i+j。
那第 i = 2 i=2 i=2, j = 1 j=1 j=1的 A i j = A 21 A_{ij}=A_{21} Aij=A21:
A 21 = ( − 1 ) 2 + 1 ⋅ M 21 A_{21}=(-1)^{2+1} \cdot M_{21} A21=(−1)2+1⋅M21
A 21 = ( − 1 ) 3 ⋅ M 21 A_{21}=(-1)^{3} \cdot M_{21} A21=(−1)3⋅M21
A 21 = − M 21 A_{21}=-M_{21} A21=−M21
那么我们将之前3x3的矩阵 A A A的每一项元素的 代数余子式 计算得出:
(上面的矩阵 A A A跑太远了,这里再复制过来,方便阅读)
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} A=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤
矩阵 A A A的伴随矩阵 A ∗ A^* A∗为每一项的 代数余字数 (注意行列 下标 是 转置 过的):
A ∗ = [ A 1 1 A 2 1 A 3 1 A 1 2 A 2 2 A 3 2 A 1 3 A 2 3 A 3 3 ] A^*=\begin{bmatrix} A_{\green 1\red 1} & A_{\green 2\red 1} & A_{\green 3\red 1} \\ A_{\green 1\red 2} & A_{\green 2\red 2} & A_{\green 3\red 2} \\ A_{\green 1\red 3} & A_{\green 2\red 3} & A_{\green 3\red 3} \end{bmatrix} A∗=⎣⎡A11A12A13A21A22A23A31A32A33⎦⎤
因为: A i j = ( − 1 ) i + j ⋅ M i j A_{ij}=(-1)^{i+j} \cdot M_{ij} Aij=(−1)i+j⋅Mij,所以式子可以调整为:
A ∗ = [ ( − 1 ) 1 + 1 ⋅ M 11 ( − 1 ) 2 + 1 ⋅ M 21 ( − 1 ) 3 + 1 ⋅ M 31 ( − 1 ) 1 + 2 ⋅ M 12 ( − 1 ) 2 + 2 ⋅ M 22 ( − 1 ) 3 + 2 ⋅ M 32 ( − 1 ) 1 + 3 ⋅ M 13 ( − 1 ) 2 + 3 ⋅ M 32 ( − 1 ) 3 + 3 ⋅ M 33 ] A^*=\begin{bmatrix} (-1)^{1+1}\cdot M_{11} & (-1)^{2+1}\cdot M_{21} & (-1)^{3+1}\cdot M_{31} \\ (-1)^{1+2}\cdot M_{12} & (-1)^{2+2}\cdot M_{22} & (-1)^{3+2}\cdot M_{32} \\ (-1)^{1+3}\cdot M_{13} & (-1)^{2+3}\cdot M_{32} & (-1)^{3+3}\cdot M_{33} \end{bmatrix} A∗=⎣⎡(−1)1+1⋅M11(−1)1+2⋅M12(−1)1+3⋅M13(−1)2+1⋅M21(−1)2+2⋅M22(−1)2+3⋅M32(−1)3+1⋅M31(−1)3+2⋅M32(−1)3+3⋅M33⎦⎤
A ∗ = [ ( − 1 ) 2 ⋅ M 11 ( − 1 ) 3 ⋅ M 21 ( − 1 ) 4 ⋅ M 31 ( − 1 ) 3 ⋅ M 12 ( − 1 ) 4 ⋅ M 22 ( − 1 ) 5 ⋅ M 32 ( − 1 ) 4 ⋅ M 13 ( − 1 ) 5 ⋅ M 23 ( − 1 ) 6 ⋅ M 33 ] A^*=\begin{bmatrix} (-1)^{2}\cdot M_{11} & (-1)^{3}\cdot M_{21} & (-1)^{4}\cdot M_{31} \\ (-1)^{3}\cdot M_{12} & (-1)^{4}\cdot M_{22} & (-1)^{5}\cdot M_{32} \\ (-1)^{4}\cdot M_{13} & (-1)^{5}\cdot M_{23} & (-1)^{6}\cdot M_{33} \end{bmatrix} A∗=⎣⎡(−1)2⋅M11(−1)3⋅M12(−1)4⋅M13(−1)3⋅M21(−1)4⋅M22(−1)5⋅M23(−1)4⋅M31(−1)5⋅M32(−1)6⋅M33⎦⎤
为了对齐,我把正负号的 代数余字数 的 + 也标出来,因为它就是带符号的 余子式:
A ∗ = [ + M 11 − M 21 + M 31 − M 12 + M 22 − M 32 + M 13 − M 23 + M 33 ] A^*=\begin{bmatrix} +M_{11} & -M_{21} & +M_{31} \\ -M_{12} & +M_{22} & -M_{32} \\ +M_{13} & -M_{23} & +M_{33} \end{bmatrix} A∗=⎣⎡+M11−M12+M13−M21+M22−M23+M31−M32+M33⎦⎤
伴随矩阵-二维的例子
那么来计算最简单的二维矩阵,求:二维矩阵的伴随矩阵。
就用我们前门最简单的2x2矩阵: A = [ a b c d ] A=\begin{bmatrix}a & b \\ c & d\end{bmatrix} A=[acbd],它的 伴随矩阵 是: A ∗ = [ d − b − c a ] A^*=\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} A∗=[d−c−ba]
下面来看看它的 A ∗ A^* A∗是怎么计算得来的(注意行列 下标 是 转置 过的):
A ∗ = [ A 11 A 21 A 12 A 22 ] A^*=\begin{bmatrix}A_{11} & A_{21} \\ A_{12} & A_{22}\end{bmatrix} A∗=[A11A12A21A22]
那看看 A 11 , A 12 , A 21 , A 22 A_{11},A_{12},A_{21},A_{22} A11,A12,A21,A22分别都是怎么计算的:
M 11 = [ a b c d ] , 删除1行1列: M 11 = [ d ] , A 11 = ( − 1 ) 1 + 1 ⋅ M 11 = ( − 1 ) 2 ⋅ [ d ] = d M_{11} =\begin{bmatrix}\color{#ff0000}a & \color{#ff0000}b \\ \color{#ff0000}c &{\color{00dd00}d} \end{bmatrix} ,\text{删除1行1列:} M_{11} =[{\color{00dd00}d}], A_{11}=(-1)^{1+1} \cdot M_{11}=(-1)^{2} \cdot [{\color{00dd00}d}]={\color{00dd00}d} M11=[acbd],删除1行1列:M11=[d],A11=(−1)1+1⋅M11=(−1)2⋅[d]=d,所以 A 11 = d \color{#ff0000}A_{11}=d A11=d
M 12 = [ a b c d ] , 删除1行2列: M 12 = [ c ] , A 12 = ( − 1 ) 1 + 2 ⋅ M 12 = ( − 1 ) 3 ⋅ [ c ] = − c M_{12} =\begin{bmatrix}\color{#ff0000}a & \color{#ff0000}b \\ {\color{00dd00}c} & \color{#ff0000}d\end{bmatrix} ,\text{删除1行2列:} M_{12} =[{\color{00dd00}c}], A_{12}=(-1)^{1+2} \cdot M_{12}=(-1)^{3} \cdot [{\color{00dd00}c}]=-{\color{00dd00}c} M12=[acbd],删除1行2列:M12=[c],A12=(−1)1+2⋅M12=(−1)3⋅[c]=−c,所以 A 12 = − c \color{#ff0000}A_{12}=-c A12=−c
M 21 = [ a b c d ] , 删除2行1列: M 21 = [ b ] , A 21 = ( − 1 ) 2 + 1 ⋅ M 21 = ( − 1 ) 3 ⋅ [ b ] = − b M_{21} =\begin{bmatrix}\color{#ff0000}a & {\color{00dd00}b} \\ \color{#ff0000}c & \color{#ff0000}d\end{bmatrix} ,\text{删除2行1列:} M_{21} =[{\color{00dd00}b}], A_{21}=(-1)^{2+1} \cdot M_{21}=(-1)^{3} \cdot [{\color{00dd00}b}]=-{\color{00dd00}b} M21=[acbd],删除2行1列:M21=[b],A21=(−1)2+1⋅M21=(−1)3⋅[b]=−b,所以 A 21 = − b \color{#ff0000}A_{21}=-b A21=−b
M 22 = [ a b c d ] , 删除2行2列: M 22 = [ a ] , A 22 = ( − 1 ) 2 + 2 ⋅ M 22 = ( − 1 ) 4 ⋅ [ a ] = a M_{22} =\begin{bmatrix}{\color{00dd00}a} & \color{#ff0000}b \\ \color{#ff0000}c & \color{#ff0000}d\end{bmatrix} ,\text{删除2行2列:} M_{22} =[{\color{00dd00}a}], A_{22}=(-1)^{2+2} \cdot M_{22}=(-1)^{4} \cdot [{\color{00dd00}a}]={\color{00dd00}a} M22=[acbd],删除2行2列:M22=[a],A22=(−1)2+2⋅M22=(−1)4⋅[a]=a,所以 A 22 = a \color{#ff0000}A_{22}=a A22=a
OK,现在 A 11 , A 12 , A 21 , A 22 A_{11},A_{12},A_{21},A_{22} A11,A12,A21,A22都计算好了。
分别代回伴随矩阵(注意行列 下标 是 转置 过的): A ∗ = [ A 11 A 21 A 12 A 22 ] = [ d − b − c a ] A^*=\begin{bmatrix}A_{11} & A_{21} \\ A_{12} & A_{22}\end{bmatrix}=\begin{bmatrix}\color{#ff0000}d & \color{#ff0000}-b \\ \color{#ff0000}-c & \color{#ff0000}a\end{bmatrix} A∗=[A11A12A21A22]=[d−c−ba]
所以你会看到这个结果就是我之前说的结果。
二维矩阵的伴随矩阵很简单,所以直接总结为之前说的简单处理:“矩阵 [ d − b − c a ] \begin{bmatrix}d & -b \\ -c & a\end{bmatrix} [d−c−ba]是怎么来的,它看起来就像是a与d交换,b,c添加了负数。”
再根据之前描述说的,伴随矩阵 和 逆矩阵 就差一个 系数值,这个系数值就是 矩阵的行列式的倒数
然后我们使用 矩阵的行列式的倒数 的结果,数乘 上 伴随矩阵 得到的就是 逆矩阵
矩阵的行列式 . 伴随矩阵 = 逆矩阵: A − 1 = 1 ∣ A ∣ ⋅ A ∗ A^{-1}=\frac{1}{|A|} \cdot A^* A−1=∣A∣1⋅A∗
如果已知 逆矩阵、矩阵行列式,那么 伴随矩阵 : A ∗ = ∣ A ∣ ⋅ A − 1 A^* = |A| \cdot A^{-1} A∗=∣A∣⋅A−1
总结 & 练习
前面说明,逆矩阵 A − 1 A^{-1} A−1作用就是将某个向量 A → \overrightarrow A A 应用了矩阵 A A A变换成的结果 B → \overrightarrow B B 的结果再反向变换回矩阵变换前的 A → \overrightarrow A A:
A ⋅ A → = B → A − 1 ⋅ B → = A → A \cdot \overrightarrow A=\overrightarrow B\\ \\ A^{-1} \cdot \overrightarrow B= \overrightarrow A A⋅A=BA−1⋅B=A
这种应用是非常广泛的,矩阵Unity中大家都应该熟悉的:GameObject 下的 Transform 组件类有 LocationPosition 与 Position:
LocationPosition是对象的局部坐标Position是世界坐标
假设有GameObject A,B,C,他们的父级关系是:A是B的父级,B是C的父级:
A
|
+--->B
|
+--->C
如果A,B有缩放、旋转、位移过,这时想在脚本里设置C的世界的标对齐到场景中某个对象D的世界位置对齐。
为了方便,直接设置某个C的Position等于D的Position即可,伪代码如下:
GameObject A, B, C, D;
void Start() {
B.Transform.SetParent(A.Transform);
C.Transform.SetParent(B.Transform);
D.Transform.SetParent(.....);
}
void C_Locate_to_D() {
C.Transform.Position = D.Transform.Position;
}
主要看:C.Transform.Position = D.Transform.Position; 这句即可,它内部处理起始用了逆矩阵来更新LocationPosition,这样外部用起来就相当方便了。
Transform 类的代码中,设置 Position 的伪代码大概如下:
class Transform {
Matrix4x4 local2worldMatrix; // local 局部坐标 变换到 world 世界坐标的矩阵
Matrix4x4 world2localnMatrix; // world 世界坐标 变换到 local 矩阵坐标的矩阵,它就是location2worldMatrix矩阵的逆矩阵
public Vector3 Position {
get => position;
set {
position = value;
localPosition= world2localnMatrix.MultiplePoint(position); // 根据 世界坐标 反向变换回 局部坐标
}
}
public Vector3 LocationPosition {
get => localPosition;
set { localPosition= value; }
}
private Vector3 position; // 世界坐标
private Vector3 localPosition; // 矩阵坐标
}
这就有点像是上面说过的:
假设有一个 局部坐标 到 世界坐标 的变换矩阵 M a t l w 2 Mat_{lw2} Matlw2(lw2==Local To World 的简写):
M a t l 2 w = [ a b c d ] Mat_{l2w}=\begin{bmatrix}a & b\\c & d\end{bmatrix} Matl2w=[acbd]
然后是 M a t l 2 w Mat_{l2w} Matl2w 的逆矩阵 M a t w 2 l Mat_{w2l} Matw2l(w2l==World To Local),它的作用是 世界坐标 到 局部坐标 的变换:
M a t w 2 l = 1 a d − b c ⋅ [ d − b − c a ] Mat_{w2l}=\frac{1}{ad-bc}\cdot \begin{bmatrix}d & -b\\-c & a\end{bmatrix} Matw2l=ad−bc1⋅[d−c−ba]
然后是 局部坐标 P o s l Pos_{l} Posl(l==Local):
P o s l = [ x l y l ] Pos_{l}=\begin{bmatrix}x_{l}\\y_{l}\end{bmatrix} Posl=[xlyl]
然后是 世界坐标 P o s w Pos_{w} Posw(w==World):
P o s w = [ x w y w ] Pos_{w}=\begin{bmatrix}x_{w}\\y_{w}\end{bmatrix} Posw=[xwyw]
那么 将 局部坐标 变换到 世界坐标:
M a t l 2 w ⋅ P o s l = P o s w Mat_{l2w} \cdot Pos_{l} = Pos_{w} Matl2w⋅Posl=Posw
[ a b c d ] ⋅ [ x l y l ] = [ x w y w ] \begin{bmatrix} a & b\\ c & d \end{bmatrix} \cdot \begin{bmatrix} x_{l}\\y_{l} \end{bmatrix} =\begin{bmatrix} x_{w}\\y_{w} \end{bmatrix} [acbd]⋅[xlyl]=[xwyw]
那么 将 世界坐标 变换到 局部坐标:
M a t w 2 l ⋅ P o s w = P o s l Mat_{w2l} \cdot Pos_{w} = Pos_{l} Matw2l⋅Posw=Posl
1 a d − b c ⋅ [ d − b − c a ] ⋅ [ x w y w ] = [ x l y l ] \frac{1}{ad-bc}\cdot \begin{bmatrix}d & -b\\-c & a\end{bmatrix} \cdot \begin{bmatrix} x_{w}\\y_{w} \end{bmatrix} =\begin{bmatrix} x_{l}\\y_{l} \end{bmatrix} ad−bc1⋅[d−c−ba]⋅[xwyw]=[xlyl]
最后的通过设置世界坐标的 P o s w Pos_{w} Posw 时,我们是已知 P o s w Pos_{w} Posw 世界坐标点的,和 M a t w 2 l Mat_{w2l} Matw2l 都是已知的,求 P o s l Pos_{l} Posl 是肯定可以的。
M a t w 2 l ⋅ P o s w = P o s l Mat_{w2l} \cdot Pos_{w} = Pos_{l} Matw2l⋅Posw=Posl
但最终的终极理解这个变换,你可以这么理解(可参考 可汗学院 里的视频:Matrix world problem: vector combination):
M a t w 2 l Mat_{w2l} Matw2l的第一列向量就是 w 2 l w2l w2l 坐标系下的 X 轴: [ x 1 y 1 ] \begin{bmatrix}x_1 \\ y_1\end{bmatrix} [x1y1],第二列向量就是 w 2 l w2l w2l 坐标系下的 Y 轴: [ x 2 y 2 ] \begin{bmatrix}x_2 \\ y_2\end{bmatrix} [x2y2],这两个轴分别缩放 [ x w y w ] \begin{bmatrix}x_w\\ y_w\end{bmatrix} [xwyw] 后,再相加(两个轴,或是两个向量相加),就等于 [ x l y l ] \begin{bmatrix}x_l \\ y_l\end{bmatrix} [xlyl]:
[ x 1 x 2 y 1 y 2 ] ⋅ [ x w y w ] = [ x l y l ] \begin{bmatrix}x_1 & x_2\\ y_1 & y_2\end{bmatrix} \cdot \begin{bmatrix}x_w\\y_w\end{bmatrix}=\begin{bmatrix}x_l \\ y_l\end{bmatrix} [x1y1x2y2]⋅[xwyw]=[xlyl]
调整为:
[ x 1 y 1 ] ⋅ x w + [ x 2 y 2 ] ⋅ y w = [ x l y l ] \begin{bmatrix}x_1 \\ y_1 \end{bmatrix} \cdot x_w + \begin{bmatrix}x_2 \\ y_2 \end{bmatrix} \cdot y_w = \begin{bmatrix}x_l \\ y_l\end{bmatrix} [x1y1]⋅xw+[x2y2]⋅yw=[xlyl]
调整为文字+公式:
W 2 L 的 轴 x ⋅ x w + W 2 L 的 轴 y ⋅ y w = 局 部 坐 标 ( W 2 L 的 轴 x 向 量 , 放 大 , 世 界 坐 标 的 x w 倍 ) + ( W 2 L 的 轴 y 向 量 , 放 大 , 世 界 坐 标 的 y w 倍 ) = 局 部 坐 标 W2L的轴_x \cdot x_w + W2L的轴_y \cdot y_w = 局部坐标\\ (W2L的轴_x向量,放大,世界坐标的x_w倍) + (W2L的轴_y向量,放大,世界坐标的y_w倍)= 局部坐标 W2L的轴x⋅xw+W2L的轴y⋅yw=局部坐标(W2L的轴x向量,放大,世界坐标的xw倍)+(W2L的轴y向量,放大,世界坐标的yw倍)=局部坐标
(但注意这里的W2L的X,Y轴,可能都是缩放、旋转过的)
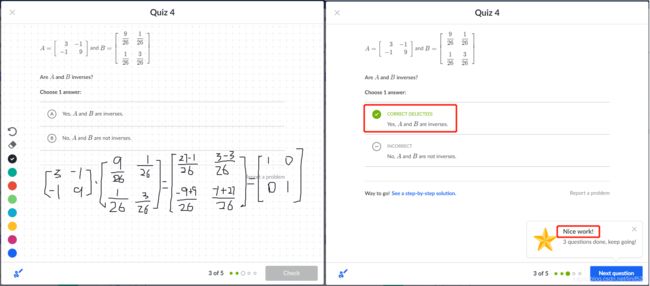
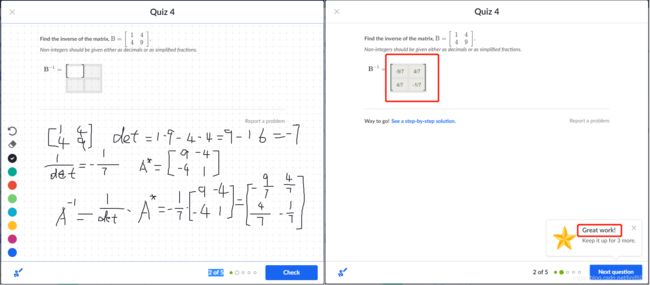
然后我在 可汗学院 的小考的里题目做测试,带上鼠标绘制(我的画板不见了)的过程与提交结果:
References
- 矩阵行列式(determinant)
- 逆矩阵(inverse)
- 伴随矩阵(adjugate、adjoint)
- 余子式(cofactor、minor)
- 代数余子式(algebraic cofactor、minor)
- 怎样用Matlab求矩阵的伴随矩阵
- 高等代数中的余子式和代数余子式的区别,书上对代数余
- 行列式determinant到底是个啥?
- Matrix world problem: vector combination