9. 类别不平衡的二次抽样（The caret package）

1. 简介(The caret package )
2. 可视化(The caret package)
3. 预处理(The caret package)
4. 数据分割（The caret package）
5. 模型训练和调参（The caret package）
6. 可用模型(The caret package )
7. train的模型标签
8. 随机超参搜索（The caret package）

9. 类别不平衡的二次抽样

内容：

• 二次抽样技术
• 重抽样中的二次抽样
• 困难性
• 使用自定义二次抽样技术

在分类问题中，
观测类别数量的不一致会对模型拟合有非常大的负面影响。解决类别不平衡的一项技术就是对训练数据进行二次抽样以缓和这样的问题。达到这种目的的抽样方法为：

• 欠抽样：在训练集中随机抽取所有类别，从而让它们的类别频率达到最小的水平。例如，假设80%的训练样本是第一类别，剩下的20%的样本为第二类别。欠抽样会随机地抽取第一类样本从而使得它的样本量与第二类相同（所以仅有总样本的40%来拟合模型）。caret有一个函数downsample来达到这个目的。
• 过抽样：随机地抽取少数类样本从而使得它的样本量和最多类相等，caret中的函数upsample就是这样的。
• 混合方法：一些技术像SMOTE和ROSE等会把大类欠采样并且在少数类中合成新的样本点。有两个包（DMwR和ROSE）来实施这些步骤。

注意到这种类型的抽样方法和单纯的把数据分割成训练集和测试集不一样。你绝对不会想人工的平衡数据；类别频率应该和显示数据保持一致。上述过程也和重抽样技术是独立的，像交叉验证和bootstrap。

实际上，可以在拟合模型之前使用训练数据抽取数据，但这种方法有两个问题：

• 第一，在模型调整过程中，由重抽样产生的外样本也在产生，并且可能不能反映出类别不平衡，但这在未来预测中可能遇得到。这可能导致更乐观的性能估计。
• 第二，二次抽样过程可能减少模型的不确定性。在不同的二次抽样下由模型得到的结果会有所不同吗？总的来说，重抽样统计量将会使模型表现比它真实的要好。

一种可选的方法就是把二次抽样放到重抽样的过程中去，也提倡放到预处理和特征选择中去。两个缺点就是他可能增加计算时间并且他可能在其他方面对分析更复杂。

9.1二次抽样技术

为了描述这些方法，让我们模拟一些类别不平衡的数据，我们模拟训练集和测试集，每个样本集中包括10000个样本，少数的类别概率为5.9%。

library(caret)

set.seed(2969)
imbal_train <- twoClassSim(10000, intercept = -20, linearVars = 20)
imbal_test  <- twoClassSim(10000, intercept = -20, linearVars = 20)
table(imbal_train$Class)
## 
## Class1 Class2 
##   9411    589

在模型调整之前，我们创建不同版本的训练集。

set.seed(9560)
down_train <- downSample(x = imbal_train[, -ncol(imbal_train)],
                         y = imbal_train$Class)
table(down_train$Class)   
## 
## Class1 Class2 
##    589    589
set.seed(9560)
up_train <- upSample(x = imbal_train[, -ncol(imbal_train)],
                     y = imbal_train$Class)                         
table(up_train$Class) 
## 
## Class1 Class2 
##   9411   9411
library(DMwR)

set.seed(9560)
smote_train <- SMOTE(Class ~ ., data  = imbal_train)                         
table(smote_train$Class) 
## 
## Class1 Class2 
##   2356   1767
library(ROSE)

set.seed(9560)
rose_train <- ROSE(Class ~ ., data  = imbal_train)$data                         
table(rose_train$Class) 
## 
## Class1 Class2 
##   4939   5061

对于这些数据，我们使用装袋分类并且使用重复5次的10折交叉验证来估计ROC曲线下的面积。

ctrl <- trainControl(method = "repeatedcv", repeats = 5,
                     classProbs = TRUE,
                     summaryFunction = twoClassSummary)

set.seed(5627)
orig_fit <- train(Class ~ ., data = imbal_train, 
                  method = "treebag",
                  nbagg = 50,
                  metric = "ROC",
                  trControl = ctrl)

set.seed(5627)
down_outside <- train(Class ~ ., data = down_train, 
                      method = "treebag",
                      nbagg = 50,
                      metric = "ROC",
                      trControl = ctrl)

set.seed(5627)
up_outside <- train(Class ~ ., data = up_train, 
                    method = "treebag",
                    nbagg = 50,
                    metric = "ROC",
                    trControl = ctrl)

set.seed(5627)
rose_outside <- train(Class ~ ., data = rose_train, 
                      method = "treebag",
                      nbagg = 50,
                      metric = "ROC",
                      trControl = ctrl)


set.seed(5627)
smote_outside <- train(Class ~ ., data = smote_train, 
                       method = "treebag",
                       nbagg = 50,
                       metric = "ROC",
                       trControl = ctrl)

我们收集重抽样结果，并且估计测试集的性能：

outside_models <- list(original = orig_fit,
                       down = down_outside,
                       up = up_outside,
                       SMOTE = smote_outside,
                       ROSE = rose_outside)

outside_resampling <- resamples(outside_models)

test_roc <- function(model, data) {
  library(pROC)
  roc_obj <- roc(data$Class, 
                 predict(model, data, type = "prob")[, "Class1"],
                 levels = c("Class2", "Class1"))
  ci(roc_obj)
  }

outside_test <- lapply(outside_models, test_roc, data = imbal_test)
outside_test <- lapply(outside_test, as.vector)
outside_test <- do.call("rbind", outside_test)
colnames(outside_test) <- c("lower", "ROC", "upper")
outside_test <- as.data.frame(outside_test)

summary(outside_resampling, metric = "ROC")
## 
## Call:
## summary.resamples(object = outside_resampling, metric = "ROC")
## 
## Models: original, down, up, SMOTE, ROSE 
## Number of resamples: 50 
## 
## ROC 
##            Min. 1st Qu. Median   Mean 3rd Qu.   Max. NA's
## original 0.8935  0.9311 0.9407 0.9410  0.9564 0.9717    0
## down     0.8937  0.9205 0.9369 0.9347  0.9549 0.9684    0
## up       0.9995  1.0000 1.0000 0.9999  1.0000 1.0000    0
## SMOTE    0.9622  0.9762 0.9808 0.9796  0.9840 0.9925    0
## ROSE     0.8764  0.8908 0.8953 0.8956  0.8999 0.9166    0
outside_test
##              lower       ROC     upper
## original 0.9134895 0.9251843 0.9368791
## down     0.9238817 0.9315572 0.9392327
## up       0.9360997 0.9437082 0.9513167
## SMOTE    0.9390808 0.9457264 0.9523720
## ROSE     0.9409081 0.9474742 0.9540403

训练集和测试集对于ROC曲线下面积的估计并没有展现出相关性。依据重抽样结果分析，可能腿短过抽样接近完美，但是ROSE表现相对较差。过抽样之所以表现那么好是因为大类中的抽样被复制并且很大一部分在模型构建的数据集和测试集中。本质上，测试集并不是真正的独立样本。
实际上，所有的抽样方法都是一样的。没有抽样的基本模型拟合的统计量和其他都是彼此相符的。

9.2重抽样中的二次抽样

caret的最近版本允许用户在使用train的时候设定二次抽样，这样它就包含在重抽样之中了。上述的四种方法在基本包中用简单的语句就能得到。如过你想使用你自己的技术，或者想改变SMOTE/ROSE中的一些参数，最后一节会展示怎样使用自定义的二次抽样方法。
增强二次抽样的方法就是使用trainControl中的选项sampling。最基本的语句就是使用带有抽样方法名称的字符串，即"down","up","smote"或"rose"。当你用SMOTE或ROSE的时候要保证DMwR包和ROSE包已经安装。
这牵涉到预处理的复杂性。二次抽样实在预处理之前还是之后？例如，如果你欠采样数据，并使用PCA进行信号提取，因子载荷应该从整个训练集中估计吗？当使用整个训练集进行估计可能是好的，但是二次抽样可能捕获一部分PCA空间。这没有明显的答案。
默认的行为就是在预处理前进行二次抽样。这可以很容易的改变，下面提供一个例子。
运行袋装树同时在交叉验证中抽样：

ctrl <- trainControl(method = "repeatedcv", repeats = 5,
                     classProbs = TRUE,
                     summaryFunction = twoClassSummary,
                     ## new option here:
                     sampling = "down")

set.seed(5627)
down_inside <- train(Class ~ ., data = imbal_train,
                     method = "treebag",
                     nbagg = 50,
                     metric = "ROC",
                     trControl = ctrl)

## now just change that option
ctrl$sampling <- "up"

set.seed(5627)
up_inside <- train(Class ~ ., data = imbal_train,
                   method = "treebag",
                   nbagg = 50,
                   metric = "ROC",
                   trControl = ctrl)

ctrl$sampling <- "rose"

set.seed(5627)
rose_inside <- train(Class ~ ., data = imbal_train,
                     method = "treebag",
                     nbagg = 50,
                     metric = "ROC",
                     trControl = ctrl)

ctrl$sampling <- "smote"

set.seed(5627)
smote_inside <- train(Class ~ ., data = imbal_train,
                      method = "treebag",
                      nbagg = 50,
                      metric = "ROC",
                      trControl = ctrl)

这儿是重抽样和检测集结果：

inside_models <- list(original = orig_fit,
                      down = down_inside,
                      up = up_inside,
                      SMOTE = smote_inside,
                      ROSE = rose_inside)

inside_resampling <- resamples(inside_models)

inside_test <- lapply(inside_models, test_roc, data = imbal_test)
inside_test <- lapply(inside_test, as.vector)
inside_test <- do.call("rbind", inside_test)
colnames(inside_test) <- c("lower", "ROC", "upper")
inside_test <- as.data.frame(inside_test)

summary(inside_resampling, metric = "ROC")
## 
## Call:
## summary.resamples(object = inside_resampling, metric = "ROC")
## 
## Models: original, down, up, SMOTE, ROSE 
## Number of resamples: 50 
## 
## ROC 
##            Min. 1st Qu. Median   Mean 3rd Qu.   Max. NA's
## original 0.8935  0.9311 0.9407 0.9410  0.9564 0.9717    0
## down     0.8902  0.9348 0.9445 0.9421  0.9507 0.9665    0
## up       0.8928  0.9211 0.9374 0.9352  0.9499 0.9637    0
## SMOTE    0.9299  0.9458 0.9528 0.9527  0.9609 0.9761    0
## ROSE     0.9189  0.9440 0.9529 0.9517  0.9597 0.9741    0
inside_test
##              lower       ROC     upper
## original 0.9134895 0.9251843 0.9368791
## down     0.9234409 0.9308037 0.9381665
## up       0.9241506 0.9340749 0.9439992
## SMOTE    0.9455682 0.9512705 0.9569727
## ROSE     0.9413039 0.9482492 0.9551946

下图展示了ROC曲线下的面积和测试集结果的不同。在每一次重抽样中重复二次抽样过程，它所产生的结果与检测集更一致。

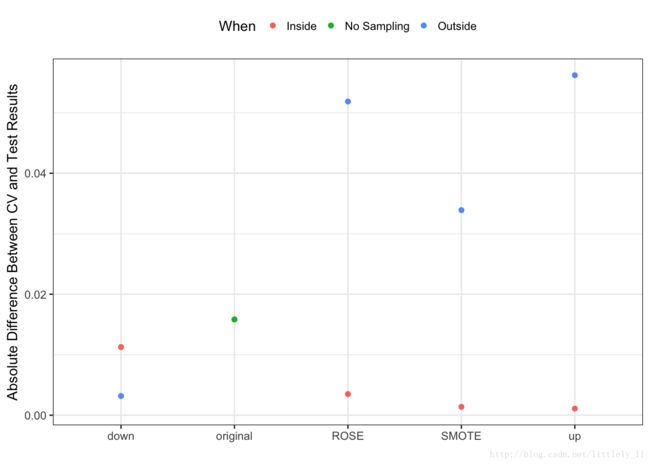
9.3 困难性

用户需要注意，在二次抽样中代码产生的问题可能很少显示出来。就如先前提到的，当抽样发生与预处理相关就是这样的一个问题，其他的如：

• 在因子变量中稀疏地展现分类变量可能导致零方差变量。
• 做抽样（例如SMOTE,downsample等）的方程可能完全使用不同的方法操作，这可能影响到你的结果。例如，SMOTE和ROSE会把你的预测输入参数转变为数据框（即使你开始使用的是矩阵）。
• 现在，二次抽样不支持抽样权重
• 如果你使用tuneLength设定搜索网格，要知道，决定网格的数据并没有被抽样。在很多案例中，这不重要，但是如果网格的创建受到样本量的影响，那么你可能用二次抽样来调整网格。
• 对于一些模型，它可能需要很多样本而非参数，样本量的减少可能让你不能拟合模型。

9.4 使用用户自定义二次抽样技术

用户有能力创建他自己类型的二次抽样过程。为了这样做，一种语句和traonControl中的参数sampling一起使用。先前，我们使用简单的字符串作为该参数的值，另一种设定参数的方法是使用一个有三个元素的列表：

• name：当train对象打印出的时候，name值这个字符串就会使用。它可是任意字符串。
• func：func是进行二次抽样的一个函数，它有参数x和y，包含了预测变量和结果变量。该函数返回具有同样名称的一个列表。
  *first：first是一个逻辑值，表明二次抽样是否先于预处理出现。FALSE意味着二次抽样函数接受x,y的抽样版本。

例如，下面是sampling参数列表的一个版本，它是使用了欠抽样：

down_inside$control$sampling
## $name
## [1] "down"
## 
## $func
## function (x, y) 
## downSample(x, y, list = TRUE)
## 
## $first
## [1] TRUE

另一个例子，假设我们想使用SMOTE但是使用10最近邻代替5最近邻，我们创建一个简单的语句：

smotest <- list(name = "SMOTE with more neighbors!",
                func = function (x, y) {
                  library(DMwR)
                  dat <- if (is.data.frame(x)) x else as.data.frame(x)
                  dat$.y <- y
                  dat <- SMOTE(.y ~ ., data = dat, k = 10)
                  list(x = dat[, !grepl(".y", colnames(dat), fixed = TRUE)], 
                       y = dat$.y)
                  },
                first = TRUE)

控制对象为：

ctrl <- trainControl(method = "repeatedcv", repeats = 5,
                     classProbs = TRUE,
                     summaryFunction = twoClassSummary,
                     sampling = smotest)