3GPP机密性和完整性算法规范128-EEA3和128-EIA3（一）----密钥生成原理

3GPP机密性和完整性算法规范128-EEA3和128-EIA3（一）----密钥生成原理

3GPP机密性和完整性算法规范128-EEA3和128-EIA3（二）----祖冲之算法的C语言实现

3GPP机密性和完整性算法规范128-EEA3和128-EIA3（三）----机密性算法(EEA3）和完整性算法（EIA3）

3GPP机密性和完整性算法规范128-EEA3和128-EIA3（四）----测试用例

3GPP机密性和完整性算法规范128-EEA3和128-EIA3（五）----文档代码资源

       最近公司要研发一款用于链路通信加密的设备，使用祖冲之算法对OSI七层中的数据链路层数据进行流式加密，对祖冲之算法的密钥生成，机密性和完整性算法都进行了学习。

1. 引言

ZUC是一个面向字的流密码。它需要一个128位的初始密钥和一个128位的初始矢量（IV）作为输入，输出一串32位字的密钥流（因此，这里每一个32位的字称为密钥字）。密钥流可以用来加密/解密。

ZUC的执行分为两个阶段：初始化阶段和工作阶段。在第一阶段，将密钥和初始向量IV初始化，也就是，时钟控制着密码运行但不产生输出（见章节3.6.1）。第二阶段是工作阶段，在这个阶段，随着每一个时钟脉冲，它都会产生一个32位字的输出（见章节3.6.2）。

1. 符号和惯例

2.1 基

在这份文档中,除非另有原因，一般整数被表示成十进制数字。我们使用前缀“0 x”表示十六进制数字,下标“2”是以二进制方式表示一个数。

 

例1整数a 可以写成不同的表示方式：

a = 1234567890                            十进制表示法

= 0x499602D2                            十六进制表示法

= 10010011001011000000010110100102      二进制表示法

 

2.2 位排序

在这份文档中，所有的数据变量在左手边提供最高有效位（字节），在右手边提供最低有效位（字节）。

 

例2  假设a=10010011001011000000010110100102   。那么它的最高有效位是1（最左边的那个位），最低有效位是0（最右边的那个位）。

 

2.3 注释

+   两个整数的加法

ab 整数a和b的乘法

= 赋值运算符

mod 整数的模运算

⊕ 整数的位异或运算

                       ⊞  模 232 的加法

a || b  字符串a和b的级联

aH   整数a的最左边16位

aL  整数a的最右边16位

a <<k  n位寄存器a 向左的k 位循环移位

a >> 1 整数a 右移一位

   (a1, a2,…, an)→(b1, b2,…, bn)  把ai 对应赋值给 bi 

例3 对于任意两个字符串a和b，由a和b级联生成的字符串c的描述同样遵循在章节2.2中定义的规则。也就是说，最高有效位在左手边，最低有效位在右手边。例如，

a=0x1234,

b=0x5678,

        于是我们有 

c = a||b =0x12345678.

例 4 假设

a=10010011001011000000010110100102

        于是我们有 

aH=10010011001011002,

aL=00000010110100102.

例 5    假设 

a=110010011001011000000010110100102.

         于是我们有 

a >> 1=11001001100101100000001011010012.

例 6  假设       a0, a1, …, a15, b0, b1, …, b15 都是整型变量，那么 

(a0, a1, …, a15)→(b0, b1, …, b15) 

         结果是 bi=ai, 0≤i≤15。

1.  算法描述

3.1 算法的总体结构

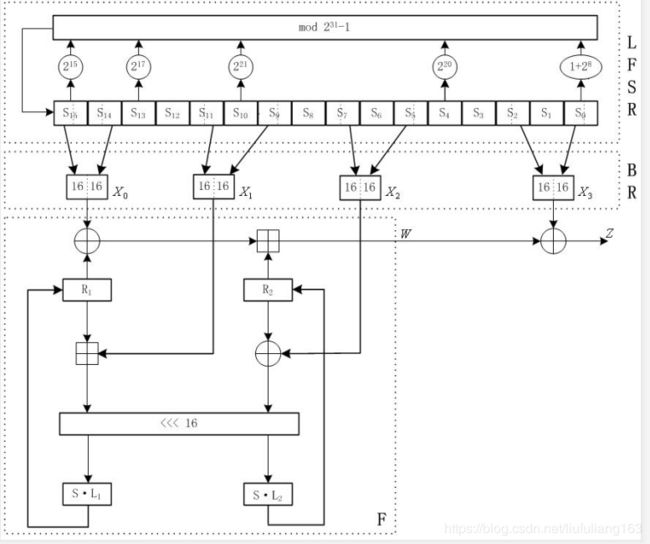
如图1，ZUC有三个逻辑层。顶层是一个16段的线性反馈移位寄存器（LFSR）。中间层是比特重组（BR），底层是一个非线性函数F。

 

 

                                                        图1 ZUC算法的总体结构

 

3.2 线性反馈移位寄存器（LFSR）

线性反馈移位寄存器（LFSR）有16个31位的单元(s0, s1,…, s15)，每个单元 si (0≤i≤15)仅限在下列集合中取值

                   {1,2,3, …,231–1}。

    LFSR包含两个操作模式：初始化模式和工作模式。

初始化模式时，LFSR接收一个31位的输入字u，u是通过去掉非线性函数F输出的32位字W的最右边的位获得的。也就是，u=W>>1。更具体地说，初始化模式工作如下：

 

LFSRWithInitialisationMode(u)
{

1. v=215s15+217s13+221s10+220s4+(1+28)s0 mod (231-1);

2. s16=(v+u) mod (231-1);

3. If s16=0, then set s16=231-1;

4. (s1,s2, …,s15,s16)→(s0,s1, …,s14,s15).

}

 

工作模式时，LFSR不再接收任何输入，其工作如下：

 

LFSRWithWorkMode()
{

1. s16=215s15+217s13+221s10+220s4+(1+28)s0 mod (231-1);

2. If s16=0, then set s16=231-1;

3. (s1,s2, …,s15,s16)→(s0,s1, …,s14,s15).

} 

 

    注意事项：由于在有限域GF(231-1)上的一个31位字符s和2i的乘积可以用s向左循环移位i位来实现，因此在上面函数的步骤1中，加法模231-1是需要的。更确切地说，函数LFSRWithInitialisationMode中的步骤1可以实现如下：v=(s15<<<3115)+(s13<<<3117)+(s10<<<3121)+(s4<<<3120)+(s0 <<<318)+s0 mod (231-1),

并且，在函数LFSRWithWorkMode里的步骤1中也需要同样的实现方式。

 

    注意事项：对于有限域GF(231-1)上的两个元素a和b，v=a+b mod (231-1)的计算可以这样来实现：（1）计算v=a+b ，（2）如果进位是1，那么使v=v+1。或者可以（如果可以抵抗可能的时序攻击，这种实现会更好的），（1）计算w=a+b，这里w是32位数值，（2）使v=（w的最低有效31位）+（w的最高有效位）。

3.3 比特重组

    该算法的中间层是比特重组。该层从LFSR单元抽取128位，形成4个32位的字。这里的前3个字会在底层的非线性函数F中使用。最后一个字将涉及产生密钥流。

    和章节3.2中一样，假设s0, s2, s5, s7, s9, s11, s14, s15 是LFSR里的8个单元。比特重组从上面的8个单元里按如下方式形成4个32位的字X0, X1, X2, X3：

Bitreorganization()
{

1． X0=s15H  || s14L;

2. X1=s11L || s9H;

3． X2=s7L || s5H;

4. X3=s2L ||s0H.

}

    注解： si是31位的整数，因此siH是指si的从第30到15位，而不是第31到16位，对于0≤i≤15。

3.4 非线性函数F

    非线性函数F包括2个32位的记忆单元R1 和 R2。假设F的输入为X0 ，X1 和 X2.，其中 X0, X1 和 X2来自比特重组的输出（见章节3.3），然后F输出一个32位的字W，函数F的具体过程如下：

F (X0, X1, X2)
{

1. W=( X0⊕R1) ⊞ R2;

2. W1= R1⊞X1;

3. W2= R2⊕X2;

4. R1=S(L1(W1L||W2H));

5. R2=S(L2(W2L||W1H)).

}

    见章节3.4.1，在这里，S是一个32×32位的S盒，L1 和L2 是在章节3.4.2里定义的线性变换。

3.4.1  S盒  S

    32×32的S盒S是由4个并列的8×8 的S盒组成，也就是说，S=(S0,S1,S2,S3)，这里S0=S2, S1=S3。S0 和 S1的定义分别在表3.1和表3.2中。

    假设x是S0 (或S1)的一个8位输入。把x像这样x=h||l写成两个十六进制数，那么表3.1（或表3.2）里第h行和l列相交的条目是S0 (或 S1)的输出。

例7 S0(0x12)=0xF9 和S1(0x34)=0xC0

    假设S盒S的32位输入X和32位输出Y如下：

X = x0 || x1 || x2 || x3，

Y = y0 || y1 || y2 || y3，

    这里xi 和yi都是字节，i=0,1,2,3。于是我们有

yi=Si(xi), i=0,1,2,3.

例8 假设X=0x12345678是S盒的32位输入，Y是S盒的32位输出。于是我们有

Y=S(X)=S0(0x12)||S1(0x34)||S2(0x56)||S3(0x78)=0xF9C05A4E. 

表 3.1. S盒 S0

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	3E	72	5B	47	CA	E0	00	33	04	D1	54	98	09	B9	6D	CB
1	7B	1B	F9	32	AF	9D	6A	A5	B8	2D	FC	1D	08	53	03	90
2	4D	4E	84	99	E4	CE	D9	91	DD	B6	85	48	8B	29	6E	AC
3	CD	C1	F8	1E	73	43	69	C6	B5	BD	FD	39	63	20	D4	38
4	76	7D	B2	A7	CF	ED	57	C5	F3	2C	BB	14	21	06	55	9B
5	E3	EF	5E	31	4F	7F	5A	A4	0D	82	51	49	5F	BA	58	1C
6	4A	16	D5	17	A8	92	24	1F	8C	FF	D8	AE	2E	01	D3	AD
7	3B	4B	DA	46	EB	C9	DE	9A	8F	87	D7	3A	80	6F	2F	C8
8	B1	B4	37	F7	0A	22	13	28	7C	CC	3C	89	C7	C3	96	56
9	07	BF	7E	F0	0B	2B	97	52	35	41	79	61	A6	4C	10	FE
A	BC	26	95	88	8A	B0	A3	FB	C0	18	94	F2	E1	E5	E9	5D
B	D0	DC	11	66	64	5C	EC	59	42	75	12	F5	74	9C	AA	23
C	0E	86	AB	BE	2A	02	E7	67	E6	44	A2	6C	C2	93	9F	F1
D	F6	FA	36	D2	50	68	9E	62	71	15	3D	D6	40	C4	E2	0F
E	8E	83	77	6B	25	05	3F	0C	30	EA	70	B7	A1	E8	A9	65
F	8D	27	1A	DB	81	B3	A0	F4	45	7A	19	DF	EE	78	34	60

表 3.2. S盒 S1

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	55	C2	63	71	3B	C8	47	86	9F	3C	DA	5B	29	AA	FD	77
1	8C	C5	94	0C	A6	1A	13	00	E3	A8	16	72	40	F9	F8	42
2	44	26	68	96	81	D9	45	3E	10	76	C6	A7	8B	39	43	E1
3	3A	B5	56	2A	C0	6D	B3	05	22	66	BF	DC	0B	FA	62	48
4	DD	20	11	06	36	C9	C1	CF	F6	27	52	BB	69	F5	D4	87
5	7F	84	4C	D2	9C	57	A4	BC	4F	9A	DF	FE	D6	8D	7A	EB
6	2B	53	D8	5C	A1	14	17	FB	23	D5	7D	30	67	73	08	09
7	EE	B7	70	3F	61	B2	19	8E	4E	E5	4B	93	8F	5D	DB	A9
8	AD	F1	AE	2E	CB	0D	FC	F4	2D	46	6E	1D	97	E8	D1	E9
9	4D	37	A5	75	5E	83	9E	AB	82	9D	B9	1C	E0	CD	49	89
A	01	B6	BD	58	24	A2	5F	38	78	99	15	90	50	B8	95	E4
B	D0	91	C7	CE	ED	0F	B4	6F	A0	CC	F0	02	4A	79	C3	DE
C	A3	EF	EA	51	E6	6B	18	EC	1B	2C	80	F7	74	E7	FF	21
D	5A	6A	54	1E	41	31	92	35	C4	33	07	0A	BA	7E	0E	34
E	88	B1	98	7C	F3	3D	60	6C	7B	CA	D3	1F	32	65	04	28
F	64	BE	85	9B	2F	59	8A	D7	B0	25	AC	AF	12	03	E2	F2

注：上面S盒S0 和S1 里的条目都是以十六进制表示的

3.4.2 线性变换L1 和L2

    L1 和L2 都是32位到32位的线性变换，其定义如下：

L1(X)=X⊕(X<<<322)⊕(X<<<3210)⊕(X<<<3218)⊕(X<<<3224)， 

L2(X)=X⊕(X<<<328)⊕(X<<<3214)⊕(X<<<3222)⊕(X<<<3230)。

3.5 密钥加载

    随着LFSR的初始化，密钥加载过程将会把初始的密钥和初始矢量扩展到16个31位的整数。假设128位的初始密钥k和128位的初始向量iv如下：

k=k0||k1||k2||…||k15

和 

iv= iv0|| iv1|| iv2||…|| iv15

    这里ki 和 ivi分别都是字节，0≤i≤15 。接着k和iv被加载到LFSR的s0, s1, …, s15 ，如下：

1. 假设D是一个由16个15位子字符串组成的240位的长常字符串：

D= d0||d1 ||…||d15,

    这里

d0 = 1000100110101112,

d1 = 0100110101111002,

d2 = 1100010011010112,

d3 = 0010011010111102,

d4 = 1010111100010012,

d5 = 0110101111000102,

d6 = 1110001001101012,

d7 = 0001001101011112,

d8= 1001101011110002,

d9 = 0101111000100112,

d10 = 1101011110001002,

d11 = 0011010111100012,

d12 = 1011110001001102,

d13 = 0111100010011012,

d14 = 1111000100110102,

d15 = 1000111101011002.

2、对0≤i≤15，使si=ki||di||ivi。

3.6 ZUC算法的执行

    执行ZUC算法分两个阶段：初始化阶段和工作阶段。

3.6.1初始化阶段

    在初始化阶段，算法调用密钥加载过程把128位的密钥k和128位的初始向量iv加载到LFSR里，（见章节3.5），并且把32位记忆单元 R1 和 R2全部清零，然后密码按如下方式操作32次：

1. Bitreorganization();                // 见章节 3.3

2. w=F(X0, X1, X2);                   // 见章节3.4

3. LFSRWithInitialisationMode(w>>1). // 见章节 3.2

3.6.2工作阶段

    在初始化阶段之后，算法进入到工作阶段。在工作阶段，算法执行一次下面的操作，并丢弃函数F的输出W。

1. Bitreorganization();          // 见章节3.3

2.    F(X0, X1, X2);                     //丢弃输出，见章节 3.4

3. LFSRWithWorkMode().     // 见章节3.2

    接着算法进入产生密钥流阶段，也就是说，对于每一次迭代，执行一次下列操作，并输出一个32位的字Z：

1. Bitreorganization();          // 见章节 3.3

2.   Z= F(X0, X1, X2)⊕X3;                   // X3的定义，见章节 3.3

3. LFSRWithWorkMode() .     //见章节 3.2