k-means聚类算法简介及正态分布实例演示
一、k-means聚类算法简介
1、什么是聚类
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常
被称为无监督学习。
2、什么是k-means聚类
K-means算法是最简单的一种聚类算法。算法的目的是使各个样本与所在类均值的误差平方和达到最小(这也是评价
K-means算法最后聚类效果的评价标准)
k均值聚类是最著名的划分聚类算法,由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚
类数目k,k由用户指定。先随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配
给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了,每个聚类的聚类中心会根据聚类
中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚
类,没有(或最小数目)聚类中心再发生变化,误差平方和局部最小。
K-means聚类算法的一般步骤:
- 初始化。输入基因表达矩阵作为对象集X,输入指定聚类类数N,并在X中随机选取N个对象作为初始聚类中心。设定迭代中止条件,比如最大循环次数或者聚类中心收敛误差容限。
- 进行迭代。根据相似度准则将数据对象分配到最接近的聚类中心,从而形成一类。初始化隶属度矩阵。
- 更新聚类中心。然后以每一类的平均向量作为新的聚类中心,重新分配数据对象。
- 反复执行第二步和第三步直至满足中止条件。
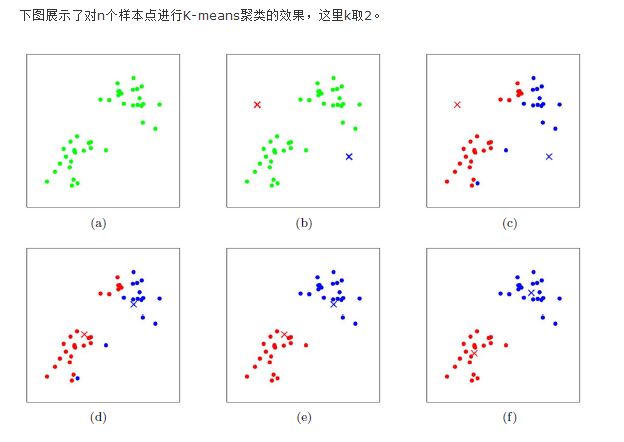
b图,红叉和蓝叉为初始聚类中心,c图,根据样本到初始聚类中心的距离对样本分类,d图,根据分类后的样本,得到新的聚类中心,这
个新的聚类中心由各类样本的中心(横纵坐标的平均值)确定。e图是重复c图的步骤,对样本再次分类,f图是重复d图的步骤,划分新的
聚类中心,不断重复这两个步骤直到满足某个终止条件。
二、正态分布实例演示
1、结果展示
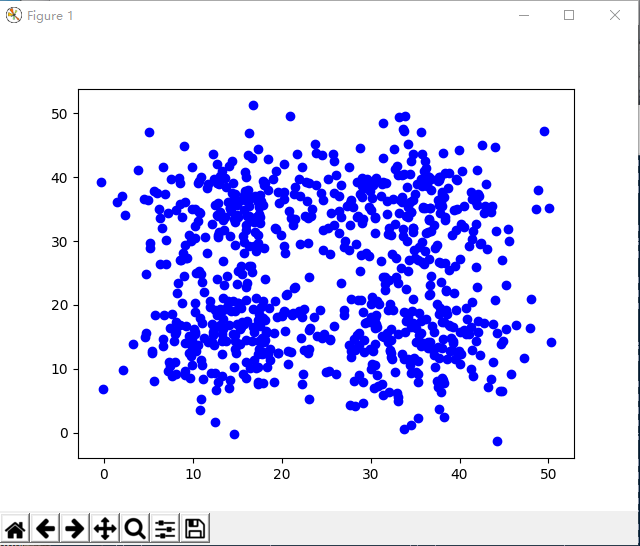
原始的点集
原始的4个正太分布点集
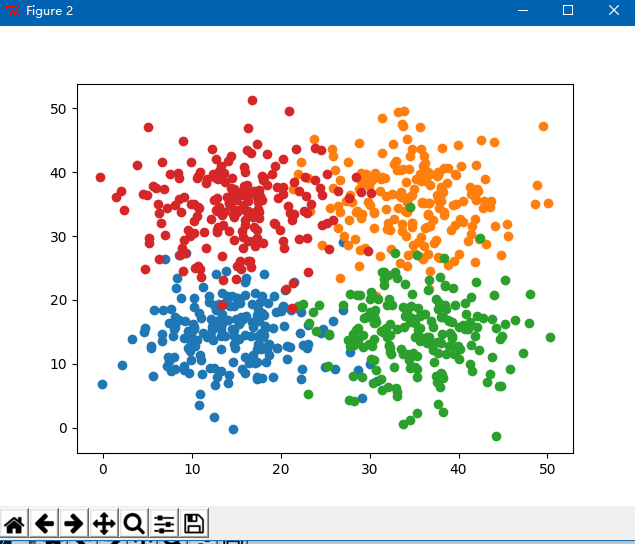
分类后的4个点集
2、完整的源代码(含注解)
# -*- coding: utf-8 -*-
import numpy
#import pylab as pl
import matplotlib.pyplot as plt
plt.figure(1)
plt.figure(2)
plt.figure(3)
import random
def distance(a, b): #定义了一个求距离平方的公式(用于比较距离大小)
return (a[0]- b[0]) ** 2 + (a[1] - b[1]) **2
A = numpy.round(numpy.random.normal(15,5.5 , 200),2) #定义4个正态分布的点集
B = numpy.round(numpy.random.normal(15,5.5 ,200), 2)
C = numpy.round(numpy.random.normal(35,5.5 , 200),2)
D = numpy.round(numpy.random.normal(35,5.5 ,200), 2)
E = numpy.round(numpy.random.normal(35,5.5 ,200) ,2)
F = numpy.round(numpy.random.normal(15,5.5 ,200), 2)
G = numpy.round(numpy.random.normal(15,5.5 ,200) ,2)
H = numpy.round(numpy.random.normal(35,5.5, 200), 2)
'''
plt.figure(1)
plt.plot(A,B,'ob')
plt.plot(C,D,'ob')
plt.plot(E,F,'ob')
plt.plot(G,H,'ob')
plt.show()
'''
'''
k1 = [15,15] #确定的初始聚类中心(已被注释掉,本次使用随机的)
k2 = [35,35]
k3 = [35,15]
k4 = [15,35]
'''
clu_k1 = [] #定义空列表,用于后续存储数据
clu_k2 = []
clu_k3 = []
clu_k4 = []
a = []
b = []
for i in A: #把4个正态分布点集的横纵坐标,分别存储在两个列表中
a.append(i) #并用 i 来排列次序
for i in C:
a.append(i)
for i in E:
a.append(i)
for i in G:
a.append(i)
for i in B:
b.append(i)
for i in D:
b.append(i)
for i in F:
b.append(i)
for i in H:
b.append(i)
k1=[random.randint(5,25) for _ in range(2)] #定义随机的初始聚类中心的位置
k2=[random.randint(25,45)for _ in range(2)]
k3=[random.randint(5,45) for _ in range(2)]
k4=[random.randint(5,45) for _ in range(2)]
while True: #不断迭代,直至循环终止
clu_k1 = []
clu_k2 = []
clu_k3 = []
clu_k4 = []
for i in range(800): #计算每个样本到聚类中心的距离
distance1 = distance(k1, [a[i], b[i]])
distance2 = distance(k2, [a[i], b[i]])
distance3 = distance(k3, [a[i], b[i]])
distance4 = distance(k4, [a[i], b[i]])
if (distance1 <= distance2 and distance1 <= distance3 and distance1 <= distance4):
clu_k1.append(i)
elif(distance2 <= distance1 and distance2 <= distance3 and distance2 <= distance4):
clu_k2.append(i)
elif(distance3 <= distance1 and distance3 <= distance2 and distance3 <= distance4):
clu_k3.append(i)
elif(distance4 <= distance1 and distance4 <= distance2 and distance4 <= distance3):
clu_k4.append(i)
#如果样本到哪一中心距离最小,就归为哪一类
k1_x = sum([a[i] for i in clu_k1]) / len(clu_k1) #对每类样本计算质心,并使之成为新的聚类中心
k1_y = sum([b[i] for i in clu_k1]) / len(clu_k1)
k2_x = sum([a[i] for i in clu_k2]) / len(clu_k2)
k2_y = sum([b[i] for i in clu_k2]) / len(clu_k2)
k3_x = sum([a[i] for i in clu_k3]) / len(clu_k3)
k3_y = sum([b[i] for i in clu_k3]) / len(clu_k3)
k4_x = sum([a[i] for i in clu_k4]) / len(clu_k4)
k4_y = sum([b[i] for i in clu_k4]) / len(clu_k4)
if(distance(k1, (k1_x, k1_y))>=0.5)and(distance(k2, (k2_x, k2_y))>=0.5)and(distance(k3, (k3_x, k3_y))>=0.5)and(distance(k4, (k4_x, k4_y))>=0.5): #判断新聚类中心与上一个聚类中心的偏移量是否为0
k1 = [k1_x, k1_y]
k2 = [k2_x, k2_y]
k3 = [k3_x, k3_y]
k4 = [k4_x, k4_y] #偏移量平方和大于0.5,则求出的质心取代原来的聚类中心
else:
break #否则迭代终止
kv1_x = [a[i] for i in clu_k1] #迭代终止后将同一类的点x,y分别以列表形式存放
kv1_y = [b[i] for i in clu_k1]
kv2_x = [a[i] for i in clu_k2]
kv2_y = [b[i] for i in clu_k2]
kv3_x = [a[i] for i in clu_k3]
kv3_y = [b[i] for i in clu_k3]
kv4_x = [a[i] for i in clu_k4]
kv4_y = [b[i] for i in clu_k4]
print '一类是:',list(zip(kv1_x,kv1_y)) #zip的作用是返回一个元组列表
print '一类是:',list(zip(kv2_x,kv2_y)) #打印出每一类的具体数值
print '一类是:',list(zip(kv3_x,kv3_y))
print '一类是:',list(zip(kv4_x,kv4_y))
plt.figure(1) #图1,打印出初始的点,并用同一颜色展示
plt.plot(A,B,'ob')
plt.plot(C,D,'ob')
plt.plot(E,F,'ob')
plt.plot(G,H,'ob')
plt.figure(2) #图2,打印出初始的点,用不同颜色(自带的)展示
plt.plot(A,B,'o')
plt.plot(C,D,'o')
plt.plot(E,F,'o')
plt.plot(G,H,'o')
plt.figure(3) #图3,打印出分类后的点,自定义颜色展示
plt.plot(kv1_x,kv1_y,'ob' )
plt.plot(kv2_x,kv2_y,'or' )
plt.plot(kv3_x,kv3_y,'og' )
plt.plot(kv4_x,kv4_y,'ok' )
plt.show()
一类是: [(12.779999999999999, 24.120000000000001), (22.260000000000002, 18.120000000000001), (12.19, 17.0), (5.4000000000000004, 12.5), (17.789999999999999, 12.380000000000001), (10.85, 3.5), (11.970000000000001, 20.559999999999999), (9.6999999999999993, 14.33), (2.1499999999999999, 9.8000000000000007), (18.129999999999999, 14.5), (9.1300000000000008, 9.0199999999999996), (13.279999999999999, 14.289999999999999), (17.550000000000001, 18.07), (16.059999999999999, 23.390000000000001), (7.4500000000000002, 10.390000000000001), (17.370000000000001, 7.9800000000000004), (14.0, 19.43), (23.09, 13.09), (14.779999999999999, 14.300000000000001), (17.870000000000001, 20.620000000000001), (8.7699999999999996, 20.359999999999999), (12.25, 15.84), (14.869999999999999, 12.460000000000001), (20.039999999999999, 18.239999999999998), (9.8300000000000001, 12.0), (8.0299999999999994, 15.390000000000001), (13.26, 15.48), (4.7400000000000002, 15.66), (20.699999999999999, 12.82), (15.98, 11.039999999999999), (16.02, 22.82), (10.199999999999999, 20.260000000000002), (11.32, 22.010000000000002), (12.02, 9.4199999999999999), (9.1699999999999999, 14.01), (15.949999999999999, 14.49), (12.42, 16.280000000000001), (5.3700000000000001, 12.789999999999999), (14.02, 16.82), (14.279999999999999, 19.039999999999999), (14.75, 15.300000000000001), (17.329999999999998, 17.690000000000001), (10.289999999999999, 15.779999999999999), (17.34, 12.300000000000001), (16.93, 11.42), (7.6100000000000003, 8.8100000000000005), (9.1400000000000006, 9.6799999999999997), (4.5899999999999999, 15.0), (22.399999999999999, 9.1199999999999992), (17.329999999999998, 10.26), (3.2999999999999998, 13.92), (9.5700000000000003, 15.15), (19.600000000000001, 12.41), (8.0500000000000007, 15.94), (18.739999999999998, 13.050000000000001), (20.390000000000001, 18.969999999999999), (13.449999999999999, 16.27), (17.539999999999999, 16.780000000000001), (12.539999999999999, 19.280000000000001), (14.699999999999999, 13.130000000000001), (20.539999999999999, 21.59), (20.260000000000002, 18.989999999999998), (18.52, 19.48), (11.06, 17.190000000000001), (18.02, 14.25), (10.970000000000001, 11.359999999999999), (11.720000000000001, 14.27), (18.210000000000001, 15.949999999999999), (15.31, 16.23), (8.0399999999999991, 11.08), (17.399999999999999, 14.33), (8.3699999999999992, 23.379999999999999), (12.470000000000001, 1.6699999999999999), (15.81, 16.969999999999999), (9.7100000000000009, 8.5299999999999994), (10.199999999999999, 18.870000000000001), (16.469999999999999, 10.119999999999999), (17.859999999999999, 7.7699999999999996), (12.32, 15.24), (19.140000000000001, 15.68), (15.140000000000001, 20.309999999999999), (6.7300000000000004, 18.399999999999999), (17.07, 10.210000000000001), (10.300000000000001, 15.51), (13.06, 19.300000000000001), (17.41, 18.66), (20.760000000000002, 10.69), (22.32, 7.6600000000000001), (13.24, 8.9399999999999995), (18.129999999999999, 24.039999999999999), (9.7899999999999991, 13.779999999999999), (13.1, 16.800000000000001), (12.880000000000001, 7.9400000000000004), (14.640000000000001, 10.300000000000001), (15.94, 8.5899999999999999), (15.949999999999999, 20.84), (20.34, 15.960000000000001), (9.9100000000000001, 14.58), (7.6799999999999997, 18.609999999999999), (13.32, 12.289999999999999), (15.31, 13.93), (8.2300000000000004, 21.890000000000001), (14.66, -0.23000000000000001), (19.120000000000001, 7.8899999999999997), (21.129999999999999, 18.370000000000001), (14.550000000000001, 15.529999999999999), (14.93, 17.100000000000001), (10.970000000000001, 5.2199999999999998), (19.609999999999999, 12.5), (18.25, 15.57), (14.15, 8.2599999999999998), (15.27, 20.199999999999999), (12.390000000000001, 13.75), (12.6, 6.7599999999999998), (8.1699999999999999, 17.309999999999999), (8.0899999999999999, 15.83), (23.030000000000001, 16.100000000000001), (11.99, 19.690000000000001), (8.5999999999999996, 16.879999999999999), (12.73, 18.41), (22.140000000000001, 14.890000000000001), (21.550000000000001, 22.789999999999999), (16.82, 16.550000000000001), (13.9, 19.640000000000001), (-0.089999999999999997, 6.8399999999999999), (15.66, 9.2200000000000006), (14.76, 19.079999999999998), (12.119999999999999, 14.15), (17.68, 19.66), (14.539999999999999, 20.550000000000001), (13.35, 17.809999999999999), (16.789999999999999, 19.34), (17.329999999999998, 16.969999999999999), (10.34, 12.76), (9.2799999999999994, 16.690000000000001), (11.01, 10.539999999999999), (10.1, 16.18), (12.470000000000001, 9.2799999999999994), (17.140000000000001, 21.02), (16.09, 17.460000000000001), (17.329999999999998, 7.6200000000000001), (10.58, 13.67), (15.380000000000001, 16.539999999999999), (22.48, 12.91), (18.489999999999998, 12.390000000000001), (15.59, 17.379999999999999), (10.83, 17.91), (6.6200000000000001, 14.720000000000001), (21.059999999999999, 12.68), (19.289999999999999, 20.649999999999999), (21.989999999999998, 18.800000000000001), (13.359999999999999, 21.129999999999999), (9.5800000000000001, 12.43), (18.66, 11.41), (15.18, 13.960000000000001), (13.880000000000001, 24.59), (22.93, 12.529999999999999), (7.3899999999999997, 16.370000000000001), (18.18, 17.629999999999999), (9.9499999999999993, 10.640000000000001), (13.77, 14.380000000000001), (17.870000000000001, 17.98), (6.6799999999999997, 13.6), (19.510000000000002, 18.16), (11.279999999999999, 14.84), (11.130000000000001, 8.4600000000000009), (7.3499999999999996, 11.140000000000001), (8.1199999999999992, 9.1899999999999995), (18.109999999999999, 12.41), (7.2699999999999996, 9.6799999999999997), (15.1, 20.300000000000001), (13.98, 20.66), (17.93, 12.56), (7.8899999999999997, 14.369999999999999), (16.850000000000001, 15.75), (16.699999999999999, 14.34), (17.739999999999998, 14.84), (14.07, 7.0300000000000002), (5.6799999999999997, 8.0999999999999996), (15.470000000000001, 19.539999999999999), (5.7400000000000002, 18.469999999999999), (13.49, 14.5), (20.09, 18.460000000000001), (18.329999999999998, 10.300000000000001), (17.420000000000002, 13.06), (21.960000000000001, 18.989999999999998), (23.120000000000001, 5.3300000000000001), (23.649999999999999, 18.16), (23.190000000000001, 16.359999999999999), (22.48, 19.34), (9.0600000000000005, 24.510000000000002), (14.99, 23.219999999999999), (23.030000000000001, 24.41), (21.370000000000001, 22.710000000000001), (13.57, 23.100000000000001), (20.59, 21.780000000000001), (13.44, 19.170000000000002), (11.039999999999999, 23.59), (21.309999999999999, 18.690000000000001)]
一类是: [(26.960000000000001, 29.109999999999999), (40.469999999999999, 35.530000000000001), (34.719999999999999, 32.049999999999997), (48.880000000000003, 37.939999999999998), (36.57, 33.280000000000001), (32.469999999999999, 36.530000000000001), (26.460000000000001, 34.740000000000002), (36.640000000000001, 35.149999999999999), (36.789999999999999, 31.559999999999999), (37.869999999999997, 36.159999999999997), (33.780000000000001, 47.310000000000002), (28.890000000000001, 27.809999999999999), (35.630000000000003, 47.049999999999997), (37.609999999999999, 39.369999999999997), (28.539999999999999, 33.920000000000002), (34.509999999999998, 34.520000000000003), (37.729999999999997, 39.57), (36.670000000000002, 35.259999999999998), (35.729999999999997, 26.710000000000001), (36.759999999999998, 39.729999999999997), (35.770000000000003, 38.609999999999999), (32.969999999999999, 41.780000000000001), (39.600000000000001, 39.740000000000002), (32.799999999999997, 32.619999999999997), (37.689999999999998, 26.760000000000002), (44.100000000000001, 31.629999999999999), (48.619999999999997, 34.960000000000001), (29.039999999999999, 38.630000000000003), (29.949999999999999, 37.850000000000001), (43.490000000000002, 34.560000000000002), (44.789999999999999, 27.120000000000001), (28.420000000000002, 33.700000000000003), (45.609999999999999, 30.010000000000002), (42.039999999999999, 37.350000000000001), (32.600000000000001, 44.420000000000002), (35.210000000000001, 39.009999999999998), (33.100000000000001, 40.310000000000002), (30.09, 34.799999999999997), (50.090000000000003, 35.189999999999998), (39.759999999999998, 35.060000000000002), (32.700000000000003, 41.32), (33.990000000000002, 33.979999999999997), (41.289999999999999, 37.670000000000002), (27.620000000000001, 28.57), (35.759999999999998, 43.670000000000002), (36.100000000000001, 28.449999999999999), (28.77, 37.380000000000003), (34.810000000000002, 31.5), (32.350000000000001, 30.98), (31.210000000000001, 37.090000000000003), (33.670000000000002, 47.609999999999999), (32.369999999999997, 28.010000000000002), (36.109999999999999, 42.539999999999999), (29.52, 28.149999999999999), (34.149999999999999, 29.960000000000001), (37.700000000000003, 40.049999999999997), (43.700000000000003, 35.439999999999998), (36.5, 31.43), (27.359999999999999, 35.520000000000003), (31.18, 26.899999999999999), (38.340000000000003, 40.600000000000001), (26.100000000000001, 40.409999999999997), (31.43, 39.310000000000002), (33.740000000000002, 40.469999999999999), (36.049999999999997, 26.420000000000002), (41.899999999999999, 36.109999999999999), (45.450000000000003, 31.960000000000001), (38.090000000000003, 43.740000000000002), (34.759999999999998, 32.060000000000002), (25.91, 37.539999999999999), (42.530000000000001, 45.020000000000003), (36.270000000000003, 31.300000000000001), (41.43, 30.309999999999999), (42.75, 34.469999999999999), (42.0, 41.149999999999999), (36.520000000000003, 40.100000000000001), (38.039999999999999, 35.43), (34.850000000000001, 28.68), (29.559999999999999, 39.729999999999997), (30.59, 39.93), (36.229999999999997, 41.43), (28.350000000000001, 29.530000000000001), (44.030000000000001, 44.810000000000002), (36.390000000000001, 38.590000000000003), (39.740000000000002, 39.539999999999999), (41.890000000000001, 32.619999999999997), (31.379999999999999, 48.520000000000003), (29.460000000000001, 38.369999999999997), (40.090000000000003, 27.190000000000001), (42.009999999999998, 35.710000000000001), (41.5, 31.550000000000001), (34.509999999999998, 42.5), (37.109999999999999, 32.490000000000002), (34.280000000000001, 27.120000000000001), (37.450000000000003, 29.440000000000001), (28.760000000000002, 25.379999999999999), (37.840000000000003, 34.469999999999999), (25.510000000000002, 34.399999999999999), (25.789999999999999, 43.630000000000003), (38.350000000000001, 33.700000000000003), (37.630000000000003, 36.409999999999997), (26.449999999999999, 31.239999999999998), (36.579999999999998, 27.199999999999999), (33.539999999999999, 36.920000000000002), (33.630000000000003, 30.859999999999999), (38.229999999999997, 36.859999999999999), (34.450000000000003, 36.090000000000003), (40.280000000000001, 40.939999999999998), (30.52, 33.700000000000003), (29.07, 39.920000000000002), (36.359999999999999, 40.140000000000001), (35.840000000000003, 35.32), (34.780000000000001, 36.509999999999998), (36.039999999999999, 40.920000000000002), (36.82, 38.009999999999998), (40.189999999999998, 32.640000000000001), (33.579999999999998, 36.060000000000002), (38.079999999999998, 37.32), (29.030000000000001, 32.82), (43.060000000000002, 28.780000000000001), (41.119999999999997, 29.260000000000002), (39.210000000000001, 30.890000000000001), (43.030000000000001, 38.969999999999999), (34.100000000000001, 38.420000000000002), (33.229999999999997, 49.399999999999999), (26.710000000000001, 33.829999999999998), (31.300000000000001, 38.960000000000001), (36.140000000000001, 35.189999999999998), (38.850000000000001, 40.590000000000003), (35.890000000000001, 35.159999999999997), (27.140000000000001, 29.989999999999998), (34.810000000000002, 43.700000000000003), (34.210000000000001, 35.329999999999998), (30.25, 39.490000000000002), (35.659999999999997, 39.780000000000001), (31.789999999999999, 36.270000000000003), (30.48, 33.670000000000002), (38.020000000000003, 37.659999999999997), (33.869999999999997, 49.659999999999997), (34.159999999999997, 45.149999999999999), (34.240000000000002, 33.789999999999999), (36.170000000000002, 39.609999999999999), (29.550000000000001, 39.57), (33.219999999999999, 34.399999999999999), (49.549999999999997, 47.25), (42.850000000000001, 35.479999999999997), (38.82, 25.5), (39.539999999999999, 26.120000000000001), (28.809999999999999, 44.539999999999999), (35.810000000000002, 29.850000000000001), (39.649999999999999, 31.739999999999998), (38.369999999999997, 33.32), (34.960000000000001, 27.399999999999999), (34.979999999999997, 37.310000000000002), (37.649999999999999, 35.590000000000003), (34.460000000000001, 40.520000000000003), (35.43, 29.109999999999999), (27.57, 41.630000000000003), (39.960000000000001, 44.25), (32.07, 32.090000000000003), (33.350000000000001, 36.460000000000001), (41.350000000000001, 36.549999999999997), (41.810000000000002, 25.91), (30.25, 38.82), (30.460000000000001, 31.27), (27.760000000000002, 36.43), (37.909999999999997, 26.600000000000001), (39.329999999999998, 34.810000000000002), (27.640000000000001, 32.5), (29.829999999999998, 35.299999999999997), (33.670000000000002, 31.899999999999999), (42.170000000000002, 37.140000000000001), (34.259999999999998, 25.379999999999999), (33.380000000000003, 25.789999999999999), (25.850000000000001, 42.469999999999999), (37.789999999999999, 40.109999999999999), (31.940000000000001, 31.09), (31.809999999999999, 34.219999999999999), (36.380000000000003, 38.939999999999998), (31.359999999999999, 42.969999999999999), (36.57, 33.399999999999999), (40.5, 32.210000000000001), (26.699999999999999, 38.840000000000003), (29.149999999999999, 33.539999999999999), (28.0, 35.340000000000003), (31.739999999999998, 39.119999999999997), (37.219999999999999, 28.899999999999999), (42.299999999999997, 29.489999999999998), (38.719999999999999, 38.350000000000001), (33.539999999999999, 40.299999999999997), (38.359999999999999, 26.550000000000001), (34.549999999999997, 34.5), (35.340000000000003, 27.079999999999998), (42.460000000000001, 29.73), (32.880000000000003, 27.350000000000001), (29.859999999999999, 27.600000000000001), (25.239999999999998, 39.740000000000002), (28.449999999999999, 39.25), (27.670000000000002, 36.020000000000003), (26.469999999999999, 37.039999999999999), (24.629999999999999, 31.710000000000001), (28.989999999999998, 36.869999999999997), (25.210000000000001, 31.989999999999998), (30.109999999999999, 36.780000000000001), (24.489999999999998, 43.5), (25.84, 32.520000000000003), (24.600000000000001, 36.450000000000003), (25.399999999999999, 27.969999999999999)]
一类是: [(24.789999999999999, 15.4), (29.199999999999999, 4.6500000000000004), (30.789999999999999, 7.2699999999999996), (25.039999999999999, 9.5600000000000005), (27.82, 11.83), (27.030000000000001, 18.48), (25.870000000000001, 16.699999999999999), (30.0, 10.01), (28.710000000000001, 9.0299999999999994), (26.100000000000001, 9.2599999999999998), (24.510000000000002, 14.779999999999999), (26.66, 23.420000000000002), (30.75, 20.640000000000001), (36.799999999999997, 24.57), (36.710000000000001, 21.649999999999999), (32.079999999999998, 23.98), (34.560000000000002, 1.1399999999999999), (31.84, 15.609999999999999), (30.52, 17.890000000000001), (47.259999999999998, 11.66), (41.869999999999997, 14.380000000000001), (33.530000000000001, 12.359999999999999), (33.939999999999998, 18.68), (32.780000000000001, 9.5800000000000001), (39.0, 14.84), (32.549999999999997, 19.25), (38.240000000000002, 17.309999999999999), (33.100000000000001, 5.6299999999999999), (40.060000000000002, 10.69), (35.399999999999999, 18.690000000000001), (32.299999999999997, 16.300000000000001), (35.920000000000002, 14.119999999999999), (38.009999999999998, 8.6199999999999992), (23.920000000000002, 15.19), (28.079999999999998, 14.640000000000001), (38.159999999999997, 14.65), (30.5, 16.43), (38.920000000000002, 16.739999999999998), (38.079999999999998, 17.41), (32.009999999999998, 14.26), (32.240000000000002, 12.5), (32.829999999999998, 24.34), (34.479999999999997, 10.6), (29.899999999999999, 13.16), (45.829999999999998, 9.2200000000000006), (35.619999999999997, 15.630000000000001), (44.890000000000001, 14.34), (44.189999999999998, -1.3600000000000001), (35.100000000000001, 16.460000000000001), (41.340000000000003, 10.029999999999999), (29.140000000000001, 7.9500000000000002), (36.659999999999997, 14.27), (30.420000000000002, 7.0099999999999998), (42.119999999999997, 17.469999999999999), (35.289999999999999, 9.1999999999999993), (28.670000000000002, 15.550000000000001), (32.18, 20.199999999999999), (30.18, 10.83), (36.189999999999998, 17.75), (31.670000000000002, 24.329999999999998), (38.880000000000003, 12.82), (38.439999999999998, 22.210000000000001), (28.510000000000002, 15.25), (28.079999999999998, 8.0399999999999991), (28.289999999999999, 4.1699999999999999), (30.469999999999999, 13.949999999999999), (32.109999999999999, 6.2999999999999998), (35.119999999999997, 9.5), (27.0, 19.25), (27.809999999999999, 12.81), (28.719999999999999, 13.800000000000001), (38.170000000000002, 8.2200000000000006), (32.009999999999998, 19.289999999999999), (30.07, 20.23), (35.670000000000002, 17.539999999999999), (28.960000000000001, 20.809999999999999), (34.0, 17.489999999999998), (41.350000000000001, 20.510000000000002), (41.969999999999999, 22.77), (35.390000000000001, 15.23), (37.450000000000003, 20.16), (43.759999999999998, 11.039999999999999), (32.32, 11.82), (39.329999999999998, 21.82), (30.219999999999999, 12.82), (42.259999999999998, 12.130000000000001), (38.030000000000001, 13.19), (42.090000000000003, 15.73), (38.509999999999998, 19.140000000000001), (39.299999999999997, 14.119999999999999), (38.25, 7.7400000000000002), (43.539999999999999, 8.3699999999999992), (31.329999999999998, 7.5800000000000001), (35.380000000000003, 2.25), (41.240000000000002, 16.609999999999999), (31.25, 15.1), (36.939999999999998, 13.050000000000001), (38.219999999999999, 2.48), (32.380000000000003, 11.56), (42.799999999999997, 17.120000000000001), (39.299999999999997, 14.4), (29.550000000000001, 17.300000000000001), (27.760000000000002, 20.949999999999999), (39.460000000000001, 11.52), (39.140000000000001, 12.949999999999999), (45.280000000000001, 16.25), (30.73, 16.530000000000001), (36.520000000000003, 21.489999999999998), (47.969999999999999, 16.34), (35.710000000000001, 13.52), (33.729999999999997, 0.56999999999999995), (33.009999999999998, 6.1500000000000004), (33.960000000000001, 22.469999999999999), (44.560000000000002, 6.5599999999999996), (36.530000000000001, 13.73), (38.460000000000001, 22.280000000000001), (40.530000000000001, 16.030000000000001), (29.09, 18.879999999999999), (33.759999999999998, 18.859999999999999), (29.350000000000001, 17.149999999999999), (31.41, 24.309999999999999), (34.189999999999998, 18.190000000000001), (37.619999999999997, 7.1699999999999999), (44.810000000000002, 6.5599999999999996), (44.009999999999998, 20.77), (43.740000000000002, 16.98), (29.25, 14.57), (39.270000000000003, 16.550000000000001), (30.620000000000001, 16.969999999999999), (24.350000000000001, 19.149999999999999), (30.059999999999999, 18.190000000000001), (46.399999999999999, 16.91), (28.210000000000001, 12.99), (44.689999999999998, 13.92), (34.530000000000001, 16.600000000000001), (31.550000000000001, 14.98), (34.609999999999999, 19.030000000000001), (37.119999999999997, 12.199999999999999), (32.140000000000001, 13.01), (37.259999999999998, 10.34), (30.73, 9.0600000000000005), (30.649999999999999, 18.48), (41.5, 8.9100000000000001), (39.579999999999998, 19.219999999999999), (33.07, 23.449999999999999), (29.289999999999999, 12.67), (29.920000000000002, 17.390000000000001), (38.799999999999997, 16.82), (38.539999999999999, 11.58), (45.200000000000003, 23.109999999999999), (40.009999999999998, 15.77), (48.079999999999998, 20.969999999999999), (28.530000000000001, 20.710000000000001), (37.770000000000003, 19.579999999999998), (37.640000000000001, 11.630000000000001), (40.770000000000003, 19.530000000000001), (43.210000000000001, 7.1399999999999997), (40.159999999999997, 12.25), (39.780000000000001, 12.09), (27.670000000000002, 4.3399999999999999), (28.370000000000001, 13.31), (34.240000000000002, 11.550000000000001), (33.090000000000003, 15.49), (37.869999999999997, 6.4100000000000001), (37.960000000000001, 23.579999999999998), (37.420000000000002, 8.0399999999999991), (30.460000000000001, 10.609999999999999), (36.670000000000002, 23.109999999999999), (25.289999999999999, 9.5899999999999999), (37.710000000000001, 3.7200000000000002), (33.719999999999999, 11.57), (34.729999999999997, 17.18), (31.620000000000001, 22.280000000000001), (34.509999999999998, 9.2799999999999994), (36.439999999999998, 14.26), (33.82, 15.74), (36.939999999999998, 16.760000000000002), (38.560000000000002, 18.59), (37.140000000000001, 15.720000000000001), (30.940000000000001, 20.170000000000002), (31.609999999999999, 23.289999999999999), (40.799999999999997, 17.73), (37.549999999999997, 13.48), (44.25, 15.539999999999999), (31.41, 5.8300000000000001), (35.329999999999998, 11.19), (50.340000000000003, 14.279999999999999), (27.620000000000001, 13.76), (35.32, 7.8899999999999997), (32.270000000000003, 14.44), (36.460000000000001, 13.27), (41.020000000000003, 15.449999999999999), (41.450000000000003, 12.880000000000001), (34.840000000000003, 11.710000000000001), (30.309999999999999, 20.719999999999999), (37.719999999999999, 18.59), (32.210000000000001, 12.779999999999999), (33.130000000000003, 4.9400000000000004), (25.440000000000001, 14.6), (40.719999999999999, 15.470000000000001), (35.079999999999998, 14.210000000000001), (34.780000000000001, 20.98), (39.950000000000003, 12.76), (30.210000000000001, 21.239999999999998), (25.379999999999999, 14.48)]
一类是: [(7.04, 26.43), (9.3699999999999992, 27.309999999999999), (8.5800000000000001, 26.98), (21.34, 37.310000000000002), (21.98, 39.719999999999999), (24.690000000000001, 28.66), (22.34, 41.549999999999997), (23.75, 45.18), (23.050000000000001, 39.100000000000001), (23.329999999999998, 33.869999999999997), (19.59, 37.740000000000002), (20.82, 34.719999999999999), (5.0199999999999996, 36.359999999999999), (20.23, 29.16), (14.44, 42.539999999999999), (20.260000000000002, 42.030000000000001), (22.010000000000002, 29.559999999999999), (8.4399999999999995, 39.939999999999998), (14.699999999999999, 32.950000000000003), (19.379999999999999, 41.0), (6.3300000000000001, 33.630000000000003), (22.969999999999999, 29.710000000000001), (22.77, 39.229999999999997), (12.25, 43.609999999999999), (18.5, 37.969999999999999), (22.629999999999999, 33.979999999999997), (10.699999999999999, 25.32), (14.32, 34.719999999999999), (9.0600000000000005, 44.859999999999999), (13.42, 33.359999999999999), (14.66, 37.020000000000003), (5.2000000000000002, 29.77), (21.280000000000001, 32.560000000000002), (9.75, 30.050000000000001), (19.239999999999998, 32.030000000000001), (13.630000000000001, 33.740000000000002), (15.119999999999999, 25.289999999999999), (21.010000000000002, 33.630000000000003), (3.8500000000000001, 41.109999999999999), (15.630000000000001, 30.870000000000001), (17.300000000000001, 33.549999999999997), (17.379999999999999, 36.119999999999997), (23.84, 43.719999999999999), (16.16, 43.530000000000001), (14.59, 33.520000000000003), (15.82, 40.869999999999997), (12.109999999999999, 32.68), (11.4, 30.690000000000001), (20.93, 49.600000000000001), (23.370000000000001, 34.969999999999999), (5.1600000000000001, 28.969999999999999), (6.5300000000000002, 32.079999999999998), (15.81, 34.880000000000003), (18.440000000000001, 42.799999999999997), (8.1600000000000001, 34.810000000000002), (17.289999999999999, 30.989999999999998), (16.550000000000001, 26.120000000000001), (19.379999999999999, 31.899999999999999), (16.649999999999999, 43.090000000000003), (12.85, 30.66), (5.0300000000000002, 47.020000000000003), (15.43, 26.109999999999999), (16.059999999999999, 33.880000000000003), (17.079999999999998, 28.399999999999999), (15.77, 29.920000000000002), (14.460000000000001, 35.75), (16.329999999999998, 29.199999999999999), (23.879999999999999, 38.829999999999998), (10.26, 34.990000000000002), (14.15, 30.850000000000001), (9.0999999999999996, 29.449999999999999), (20.210000000000001, 37.670000000000002), (10.74, 39.43), (12.52, 35.689999999999998), (16.609999999999999, 25.149999999999999), (10.619999999999999, 33.189999999999998), (7.5199999999999996, 39.780000000000001), (16.280000000000001, 35.439999999999998), (18.109999999999999, 39.119999999999997), (13.359999999999999, 26.859999999999999), (10.26, 32.310000000000002), (9.2100000000000009, 27.309999999999999), (14.140000000000001, 35.119999999999997), (15.109999999999999, 33.789999999999999), (16.93, 29.23), (17.550000000000001, 32.829999999999998), (8.6799999999999997, 27.050000000000001), (14.369999999999999, 37.490000000000002), (12.91, 38.960000000000001), (6.2999999999999998, 26.460000000000001), (20.390000000000001, 28.190000000000001), (2.02, 37.109999999999999), (14.050000000000001, 41.810000000000002), (22.91, 33.640000000000001), (17.489999999999998, 35.340000000000003), (4.4900000000000002, 36.57), (15.73, 37.240000000000002), (18.030000000000001, 38.710000000000001), (15.949999999999999, 40.0), (14.99, 35.649999999999999), (21.670000000000002, 43.670000000000002), (13.279999999999999, 40.920000000000002), (13.94, 36.140000000000001), (6.6200000000000001, 41.579999999999998), (16.52, 36.810000000000002), (12.890000000000001, 36.039999999999999), (10.970000000000001, 24.91), (10.289999999999999, 30.41), (16.27, 34.0), (14.220000000000001, 35.229999999999997), (13.1, 40.219999999999999), (4.6900000000000004, 24.890000000000001), (22.030000000000001, 37.090000000000003), (17.73, 36.32), (17.039999999999999, 31.460000000000001), (12.970000000000001, 31.449999999999999), (6.0300000000000002, 37.539999999999999), (15.91, 36.369999999999997), (12.890000000000001, 31.02), (17.920000000000002, 35.579999999999998), (10.720000000000001, 34.590000000000003), (6.8300000000000001, 37.380000000000003), (13.49, 31.760000000000002), (15.210000000000001, 36.289999999999999), (16.98, 37.049999999999997), (6.1799999999999997, 34.990000000000002), (14.779999999999999, 37.380000000000003), (-0.37, 39.259999999999998), (22.82, 36.219999999999999), (9.9499999999999993, 41.549999999999997), (8.6199999999999992, 39.079999999999998), (16.579999999999998, 33.409999999999997), (19.719999999999999, 36.039999999999999), (14.710000000000001, 29.34), (11.65, 28.140000000000001), (17.600000000000001, 33.780000000000001), (8.5600000000000005, 35.799999999999997), (7.0199999999999996, 30.170000000000002), (12.779999999999999, 42.030000000000001), (15.52, 24.84), (15.9, 37.899999999999999), (17.489999999999998, 34.270000000000003), (16.739999999999998, 51.25), (2.3700000000000001, 34.090000000000003), (19.960000000000001, 30.940000000000001), (12.869999999999999, 33.979999999999997), (10.960000000000001, 40.079999999999998), (14.5, 39.060000000000002), (13.48, 39.859999999999999), (13.029999999999999, 34.520000000000003), (11.56, 38.350000000000001), (16.370000000000001, 26.18), (13.74, 38.5), (1.52, 36.130000000000003), (20.27, 36.539999999999999), (9.6099999999999994, 30.98), (24.420000000000002, 37.5), (18.010000000000002, 28.960000000000001), (10.85, 34.420000000000002), (10.57, 39.170000000000002), (12.710000000000001, 39.109999999999999), (10.34, 25.010000000000002), (21.469999999999999, 38.479999999999997), (15.98, 31.73), (16.91, 33.009999999999998), (7.2599999999999998, 34.329999999999998), (12.369999999999999, 39.710000000000001), (9.9600000000000009, 35.049999999999997), (15.75, 28.129999999999999), (8.8100000000000005, 33.840000000000003), (8.9499999999999993, 28.109999999999999), (5.6299999999999999, 37.810000000000002), (12.77, 34.049999999999997), (14.94, 34.090000000000003), (17.059999999999999, 33.740000000000002), (21.539999999999999, 33.420000000000002), (16.469999999999999, 36.880000000000003), (17.329999999999998, 29.670000000000002), (17.600000000000001, 37.170000000000002), (16.329999999999998, 46.950000000000003), (16.239999999999998, 37.960000000000001), (17.920000000000002, 39.359999999999999), (9.0800000000000001, 36.079999999999998), (16.0, 32.549999999999997), (17.379999999999999, 44.399999999999999), (18.969999999999999, 39.770000000000003), (11.699999999999999, 38.920000000000002), (13.67, 39.82)]