基于适度贪婪调参策略下的XGBoost集成模型
本篇博客写作背景：
在大三上学期的时候，在本学校某老师的ML相关课程的介绍下，参加了“融360”天机智能金融算法挑战赛的算法竞赛，该竞赛在2018年的选题有三道，我选的是第二道题“拒绝推断”。并且取得了比较好的成绩，在这里分享一下我的比赛思路。如有做的不好的地方，还请走过路过的大佬们批评指正~~
本篇博客目录如下：
本篇博客写作背景：
本篇博客目录如下：
一、数据预处理和数据分析
1.1数据筛选
1.2缺失值处理
二、算法动机与模型介绍
2.1算法动机
2.2数据复筛选
2.3贪心算法调参
3.4XGBoost集成学习
3.5权重分配
三、实验结果与模型验证
3.1实验结果
四、总结与补充
4.1算法总结
4.1补充说明
4.2详细文件及代码我放在了github上面
一、数据预处理和数据分析
1.1数据筛选
本赛题发放的训练集数据量比较庞大，约10万条带有6745列特征属性的数据，处理起来十分费时。其实数据量大带来的处理费时问题不大，我可以多花时间进行处理；但是巨大的数据量还带来一个硬件上的问题，因此必须对数据进行数据规模上的筛选处理。
- 对于行数据的筛选：
题目中给的训练集是共99998(行)*6749(列)数据，由于题目中也说了“信用评分top30%的样本给出每个样本是否逾期，后70%只有3000个是给是否逾期。”我统计共有33464行数据的“label”行标签是给出数据值的，这里我就只选取带有“label”标签的33464行数据作为筛选后的训练集样本数据。
- 对于列数据的筛选：
题目中给的6749列数据中共有6745个特征属性填列（取值分别为：f1, f2, ……, f6745），除掉这6745列之外，还有列标签名为[‘id’, ‘loan_dt’, ‘lebal’, ‘tag’]四列数据，我将其中[‘id’, ‘loan_dt’, ‘tag’]三列数据删除掉，这样只保留‘label’和6745个特征属性列的取值，因此现在的训练样本规模是：33464*6746。
1.2缺失值处理
样本中含量大量的缺失的值，我统计过没有任何一行数据是完整地包含所有6745列特征属性。我尝试过采用“0”填补缺失值，或者是“平均值”、“中位数”、“众数”填补缺失值，耗费巨大时间，然而比较效果之后，反而是XGBoost自身填补缺失值的方法效果最佳。因此采用的是不填补样本缺失值，直接将带有缺失值的训练样本数据（33464*6746）带入XGBoost算法模型中。关于XGBoost的缺失值填补方法，陈天奇博士在论文中已经解释很清楚，具体细节可以参考陈天奇博士的论文。
2.3数据分析：
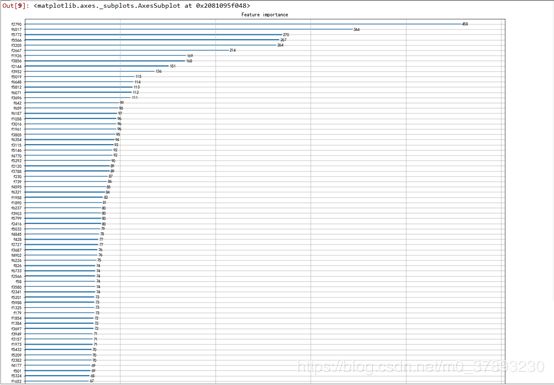
在对训练集初步使用XGBoost的时候生成的特征值得分(Feature importance)图像如下（因为有6745个特征，整张图片有80cm长，我只截取前60个特征值图片放在报告里，原图在附件中）：
二、算法动机与模型介绍
2.1算法动机
众所周知，xgboost由于其优秀的表现被证明在很多任务上能够取得很好的表现。然而，xgboost的使用通常面临着两个比较大的困难：1，xgboost的参数比较多，调参面临较大的困难 2. xgboost对应于gradient boosting的思想，有着较大的过拟合风险。同时，本赛题涉及到的训练和测试数据有着“分布不一致”的问题，所以过拟合风险尤其要注意。最终我设计了一个算法，这个算法在一定程度上缓解了上述两个问题：对于第一个问题，算法采用了贪婪的思想来进行调参；对于第二个问题，算法采用了集成学习来增加稳健性。
在下面的部分，我们首先介绍如何对数据进行预处理和预观察，然后介绍算法的详细思路和训练细节，以及展示我们的实验结果，最后我们给出算法总结和补充说明。
2.2数据复筛选
我的笔记本电脑配置如下：
但是在进行调参的时候，我将在“数据预处理”环节中我筛选后的训练样本数据(规模：33464*6746)带入我的调参代码中，电脑因为数据量巨大程序运行不了。因此我只好将数据再进行一步筛选。我的筛选条件是将特征属性列中缺失值超过10%的训练样本数据删除掉（即将掉缺失675列特征属性的行数据删除掉），这样筛选之后我得到的训练样本数据规模为：2456*6746。说明一下，这里得到的2456*6746训练样本数据仅用作XGBoost调参时使用，在训练模型过程中用到的训练样本数据仍然是我们第一步“数据预处理”时筛选得到的33464*6746规模的训练样本数据。
2.3贪心算法调参
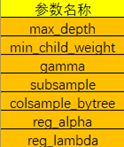
我主要调整的XGBoost参数如下：
利用网格搜索的方式来同时调优上面的参数是一个巨大计算量的工作，这限制了每个参数可取值空间的大小。所以我们采用贪婪的方式对参数进行分组后分步调优，并且每次并不是只依赖于最优的那个参数子集，而是会选取若干个最优的参数子集（所以我称算法为“适度贪婪”）。主要操作细节如下：
参数调整的取值范围：
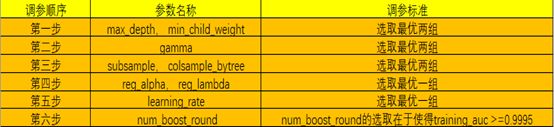
基于贪心算法思想，我将XGBoost的调参过程分为六个步骤，在每一步调参后取得的局部最优参数条件下，再进行下一步的对其他参数调优；以此类推，直至调整完所有参数。
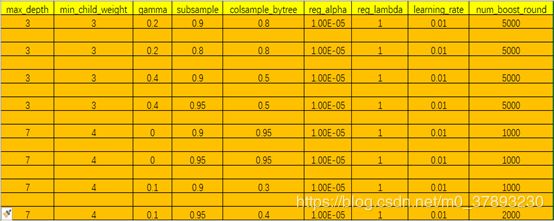
说明：对于reg_alpha，reg_lambda的两组参数调参范围如下，但是考虑到这两组参数是正则化的参数，并且如果再次进行8次调参的话太耗时，我没有再次对它进行8次调参，在目前得到的最优一组参数下（max_depth=3，min_child_weight=3，gamma=0.2，subsample=0.9，colsample_bytree=0.8）调整参数。详细数据如下：
3.4XGBoost集成学习
尽管xgboost表现一直很优越，但由于boosting算法的思想是追求“低偏差”而接受“高偏差”的特点，所以我担心如果用单一的xgboost将在本赛题上表现的不好。因为本赛题的问题涉及到“数据分布不一致”，所以过拟合的风险比较大。于是我决定利用xgboost的集成来增加模型的稳健性。我在调参的过程中采用不是单取最优的那一组参数，而是选取较优的几组参数模型。调参步骤是：
- 先调整max_depth和min_child_weight两组参数，选择得分最优的2组参数；
- 其次我们再调整gamma参数，我们留下最优的2组数据；
- 然后我调整subsample和colsample_bytree这两组参数，选择最优的2组数据；
- 接着对两组正则系数reg_alpha，reg_lambda进行调整参数，选取最优一组数据；
- 因此现在共有2*2*2*1=8组数据。最后再次调整learning_rate和num_boost_round的参数，选取最优的一组参数。
当然在这里调参步骤中也可以考虑分为不同的“步骤组”，所谓步骤组，就是上面列出的9个参数，可以随机分为几个步骤，并且在每一次的步骤中进行调整一个或者两个参数，例如上面的五步调整可以作为一种步骤组；“第一步：max_depth；第二步：min_child_weight；第三步：gamma；第四步：subsample，colsample_bytree；第五步：reg_alpha，reg_lambda；第六步：learning_rate，num_boost_round”这样的参数组调整又可以说是另一种“步骤组”。
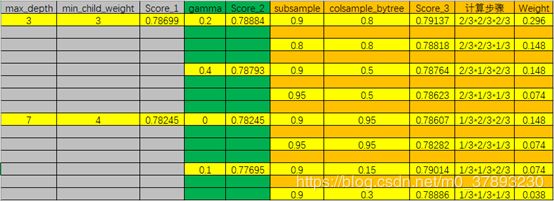
综上所述，最终我得到共8组最靠前的XGboost实验参数如下图：
3.5权重分配
将以上8组不同的参数带入XGBoost中学习，这里学习时使用的数据集是“数据预处理”后得到的33464*6746规模的训练集，采用“sklearn.cross_validation”工具包中 train_test_split将训练集分成train_x, tran_y, test_x, test_y,并且test_size = 0.3。（8组参数学习到的实验模型我已将model保存下来，放在附录中。读者可以使用“bst = xgb.Booster(model_file='文件路径')”这一行代码可以迅速得到我报讯的实验模型，这样可以节约时间。）
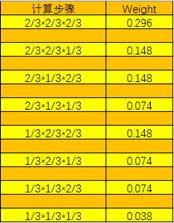
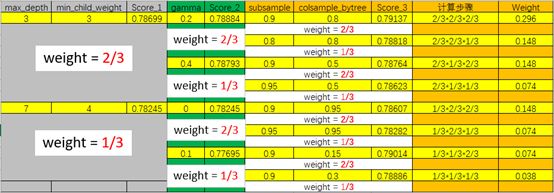
我的最终实验方法是在使用以上方法调参后得到的8组XGBoost实验参数，进行对训练集学习之后得到8个训练model，根据调参时参数的最优和次优比较排序，最优的分配权重2/3，次优的分配权重1/3，这样前三步调整参数后得到8组实验参数的权重计算步骤如下表格：
上图是加入权重分配计算引导后有些乱，下图是没有权重计算过程的表格，方便理解。
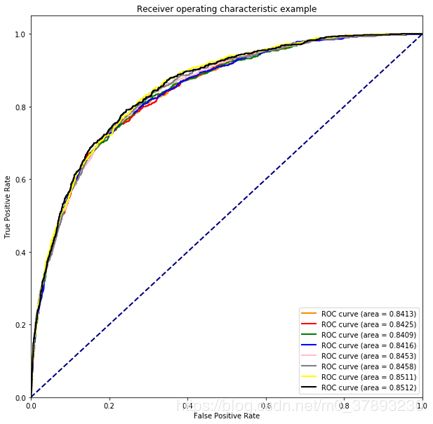
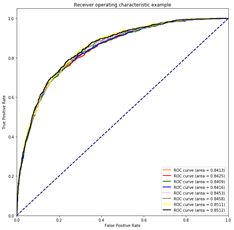
8组参数模型下的训练集的ROC曲线如下：
三、实验结果与模型验证
3.1实验结果
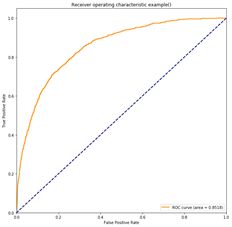
8组参数模型对应的ROC曲线上面已有。然后我将8组训练集的预测参数进行权重相加，得到的ROC曲线如下：
可以看到在进行加权之后，新模型预测的结果AUC为0.8518，得分比较最初8组模型得分都上升了至少0.06%，从而验证该模型有效。
接下来再次将8组实验参数带入XGBoost后对全部的训练集进行学习，因为在上一步学习模型的时候采用train_test_split方法将0.3的训练集数据用来测试模型，所以上面原始的实验模型只学习了训练集中22424（33464*0.7 = 22424）行数据。因此在将模型运用到赛题发放的是验证集和测试集的时候，我将8组参数分别使用33464*6746的训练集再次进行学习，得到的学习模型同样保存在了附录中。这样做的目的是提高模型的泛化能力，避免欠拟合。
四、总结与补充
4.1算法总结
该算法在稳定性和优化性上都表现出了优势：
稳定性：
这种在XGBoost基础上的适度集成学习算法要比单组训练集模型上取得的最优参数模型要稳定的多，因为这种模型一定程度上平衡了算法的局部最优解的的风险。此外，这种XGBoost适度集成的学习方法不仅保证XGBoost算法的自身优势不变之外，还能够保证算法能够在更多的情况下寻找全局最优解提供保障，以防困于贪心算法调参时的陷入局部最优解的过拟合风险。
优化性：
这种算法确实能够对于单个参数组的XGBoost的训练模型带来提升效果，如下两图：
上图体现8组实验参数模型与最终的集成学习模型对比，显然集成学习的效果更佳。
4.1补充说明
- 在本例中，我采用的调参步骤分为六步，但是涉及到权重分配的步骤只是前三步。只要调参过程中选取不单是最优的参数时，那么就会涉及到权重分配。如果涉及到分配权重的步骤记为数列a；
- 本例中涉及到权重分配的步骤中选取的都是2组，如果每一步选取的参数个数不同，对应的个数记为数列b；
- 那么最终会产生 Πbi
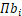组参数模型。
4.2详细文件及代码我放在了github上面
需要的可以点击github访问或下载。
详细文件解释如下：
- 【1】XGBoost调参的程序文件；
- 【2】调参过程的结果我截图保存了，因为这个调参程序文件太大，运行一次很费时间，所以我这几天自己运行了一遍并将程序结果截图保存，以便评委审核；
- 【3】数据筛选的程序文件，筛选出带有‘label’值的33464*6749数据；
- 【4】将模型泛化后的程序文件，即用全部的33464*6749数据进行学习的程序文件；
- 【5】所用数据规模是22424*6749的训练模型程序文件，；
- 【6】训练出的8组模型进行集成学习的程序文件；
- 【7】最终提交在测试集上的数据文件，是【12】的程序文件预测的数据；
- 【8】8组【5】中学习出的模型的ROC曲线图（合并在一张图中）；还有特征得分图是6745个特征的Feature importance图，大概有80cm长，需放大后才能看的清晰；
- 【9】在【6】中程序文件生成的集成学习模型ROC曲线；
- 【10】我将【4】中程序学习到的模型全部保存下来，方便使用；
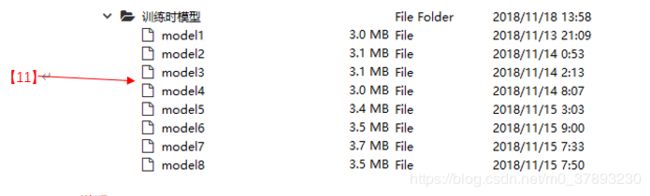
- 【11】我将【5】中程序学习到的模型全部保存下来，方便使用；
- 【12】泛化时的8组模型进行集成学习的程序文件，并生成最终的测试集预测结果；
PS：第一写的正式博客，肯定是有很多不足的地方，还请各位大佬见谅~~~