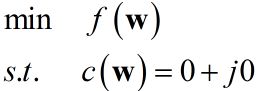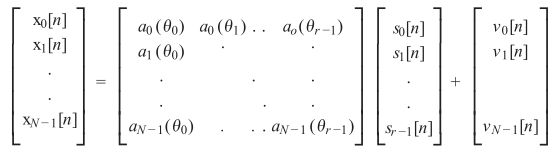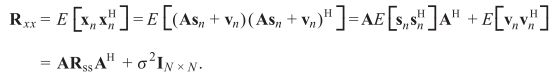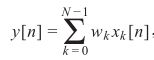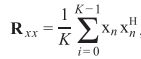自适应滤波:维纳滤波器——LCMV及MVDR实现
自适应滤波:维纳滤波器——LCMV及MVDR实现
作者:桂。
时间:2017-03-24 06:52:36
链接:http://www.cnblogs.com/xingshansi/p/6609317.html
声明:欢迎被转载,不过记得注明出处哦~
【读书笔记03】
前言
西蒙.赫金的《自适应滤波器原理》第四版,上一篇看到维纳滤波基本形式:最优化问题,且无任何条件约束。这次看到有约束的部分,简单整理一下思路:
1)拉格朗日乘子法;
2)线性约束最小方差滤波器(Linearly constrained minimum-variance,LCMV);
3)谱估计之MVDR算法(Minimum variance distortionless response ,MVDR);
内容为自己的学习总结,如有错误之处,还请各位帮忙指出!
一、拉格朗日乘子法
学习到含有约束条件的Wiener Filter,拉格朗日乘子法是解决:将含约束条件的优化问题转化为无约束条件优化问题的途径,故先梳理一下。
A-只含一个等式约束的最优化
实函数f(w)f(w)是参数向量ww的二次函数,约束条件是:
wHs=gwHs=g
其中ss是已知向量,gg是复常数。例如在波束形成应用中ww表示各传感器输出的一组复数权值,ss是一个旋转向量。假设该问题是一个最小化问题,令c(w)=wHs−g=0+j0c(w)=wHs−g=0+j0可以描述为:
所谓拉格朗日乘子法,就是引入拉格朗日乘子:将上述约束最小化问题转化为无约束问题,定义一个新的实函数:
h(w)=f(w)+λ1Re[c(w)]+λ2Im[c(w)]h(w)=f(w)+λ1Re[c(w)]+λ2Im[c(w)]
现在定义一个复拉格朗日乘子:
λ=λ1+λ2λ=λ1+λ2
h(w)h(w)改写为:
h(w)=f(w)+Re[λ∗c(w)]h(w)=f(w)+Re[λ∗c(w)]
至此,无约束优化问题转化完成,利用偏导求参即可,其实这是一个简化的形式,分别求解λ1λ1、λ2λ2也是一样的。
B-包含多个等式约束的最优化
实函数f(w)f(w)是参数向量ww的二次函数,约束条件是:
wHsk=gkwHsk=gk
其中k=1,2...Kk=1,2...K,方法同单个约束情况相同,求解伴随方程:
∂f∂w∗+∑k=1K∂∂w∗(Re[λ∗kck(w)])=0∂f∂w∗+∑k=1K∂∂w∗(Re[λk∗ck(w)])=0
此时与多个等式约束联合成方程组,这个方程组定义了ww和拉格朗日乘子λ1λ1、λ2λ2...λKλK的解。
二、线性约束最小方差滤波器
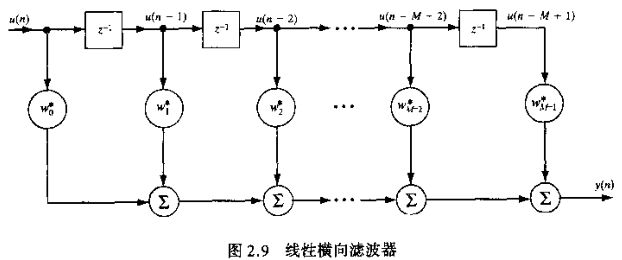
之前看到的维纳滤波都是基于最小均方误差准则,而没有添加任何约束,此处考虑含有线性约束情况下的方差滤波器,文中给了一个图:
其中x(n)x(n)为输入信号(即uu,为了与下文统一,用xx表示),wiwi为权重,y(n)y(n)为滤波器输出:
y(n)=∑k=0M−1w∗kx(n−k)y(n)=∑k=0M−1wk∗x(n−k)
这个优化问题如果没有约束可以表述为:
argminwJ=E[yHy]argminwJ=E[yHy]
假设θ0θ0为目标达到角,希望对该角度特殊处理:如果该角是目标角,希望其幅度保持不衰减,即∑k=0M−1w∗ke−jkθ0=1∑k=0M−1wk∗e−jkθ0=1;反之,如果是干扰信号,希望其幅度衰减为0,即∑k=0M−1w∗ke−jkθ0=0∑k=0M−1wk∗e−jkθ0=0;无论是0还是1,都是对优化问题的一种约束形式,写出更一般的约束形式:
∑k=0M−1w∗ke−jkθ0=g∑k=0M−1wk∗e−jkθ0=g
gg是一个复增益。利用拉格朗日乘子法给出约束条件下准则函数(暂不考虑噪声情况):
J=wHRxxw+Re[λ∗[wHs(θ0)−g]]J=wHRxxw+Re[λ∗[wHs(θ0)−g]]
其中s(θ0)=[1,e−jθ0,...,e−j(M−1)θ0]s(θ0)=[1,e−jθ0,...,e−j(M−1)θ0],MM是权向量ww的个数,则到系数解:
λ=−2gsH(θ0)R−1s(θ0)λ=−2gsH(θ0)R−1s(θ0)
对应最优权向量:
wopt=g∗R−1s(θ0)sH(θ0)R−1s(θ0)wopt=g∗R−1s(θ0)sH(θ0)R−1s(θ0)
以权向量woptwopt表征的波束形成器称为线性约束最小方差(LCMV, linearly constrained minimum-variance)波束形成器,也称LCMV滤波器。
三、LCMV应用——MVDR算法
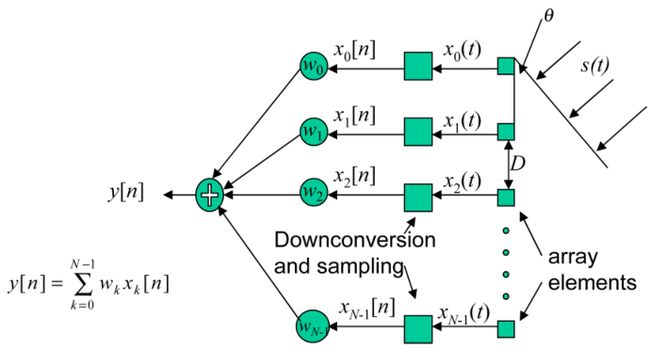
实际应用中信号掺杂了噪声。假设原信号s(t)s(t),接收器收集的是不同时延的混合信号,经过采样量化后得x(n)x(n),现在希望通过自适应权重ww输出符合需求的yy,假设通道个数为NN,给出接收通道模型:
写成矩阵形式:
![]()
进行相关矩阵求解:
可以发现如果wHwwHw为定值,则噪声对最优权值的求解无影响,LCMV可用。
给出混合模型:
对应准则函数(此处g=1g=1):
借助LCMV的分析,得出MVDR最优权重:
实际应用中,通常用时间换空间,借助遍历性近似求解相关矩阵:
给出代码:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
|
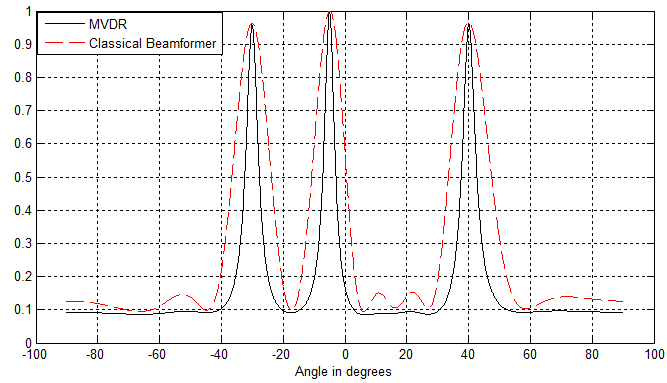
对应结果图:
噪声较大时:
二者就比较接近,可以发现:
- 信号与噪声不相关、且噪声为白噪声时,仍能求解最优权值;
- 噪声较大时,MVDR与无约束最优滤波效果接近,此时MVDR的优势不再明显,这也容易理解,噪声占主要成分时对波束的约束保留效果不再明显。
两点补充:
1)因为LCMV中有矩阵求逆一项,所以补充说明一点:默认不同角度信号不相干,只记录学习的理论知识,不论及技术细节处。
2)基于窄带分析。如果是宽带,则可以划分多个自带,或者利用聚焦矩阵预处理,窄带才有如下近似(且一个频带内才可以用一个频率表征):
参考:
Jeffrey Foutz, Andreas Spanias, and Mahesh K. Banavar《Narrowband Direction of Arrival Estimation for Antenna Arrays》.
Simon Haykin 《Adaptive Filter Theory Fourth Edition》.