变分推断二(基于随机梯度求解分布Q)
高方差的问题
根据上一节变分推断一(根据平均场理论求解Q)我们得到了需要求解的分布 Q Q Q的函数。
L ( Q ) = ∫ Z Q ( Z ) l o g P ( X , Z ) Q ( Z ) d Z Q = E Q ( Z ) [ l o g P ( X , Z ) − l o g Q ( Z ) ] (1) \begin{aligned} \tag{1} L(Q) = & \int_{Z} Q(Z)log{P(X,Z) \over Q(Z)} dZ \\Q = & E_{Q(Z)}[logP(X, Z) - logQ(Z)] \end{aligned} L(Q)=Q=∫ZQ(Z)logQ(Z)P(X,Z)dZEQ(Z)[logP(X,Z)−logQ(Z)](1)
我们最终的目的是求解 Q Q Q,在实际中 Q Q Q分布是有参数的,参数记为 φ \varphi φ,只要求解了参数 φ \varphi φ,也就求得了分布 Q Q Q。因此我们可以将(1)式进一步写成关于未知参数 φ \varphi φ的函数。即
L ( φ ) = E q φ ( z ) [ l o g p ( x i , z ) − l o g q φ ( z ) ] (2) \tag{2}L(\varphi) = E_{q_{\varphi}(z)}[logp(x^{i},z) - logq_{\varphi}(z)] L(φ)=Eqφ(z)[logp(xi,z)−logqφ(z)](2)
其中 x i x^{i} xi表示第i个样本,并且将(1)式中的大写字母全部转化为小写。这对推导并没有影响。
既然题目是用梯度来求未知参数 φ \varphi φ,那么就要对(2)式求关于 φ \varphi φ的导数。
∇ φ L ( φ ) = ∇ φ ( E q φ ( z ) [ l o g p ( x i , z ) − l o g q φ ( z ) ] ) = ∇ φ ∫ z q φ ( z ) [ l o g p ( x i , z ) − l o g q φ ( z ) ] d z = ∫ z ∇ φ q φ ( z ) [ l o g p ( x i , z ) − l o g q φ ( z ) ] d z + ∫ z q φ ( z ) ∇ φ [ l o g p ( x i , z ) − l o g q φ ( z ) ] d z = A + B (3) \begin{aligned} \tag{3} \nabla_{\varphi}L(\varphi) = & \nabla_{\varphi}(E_{q_{\varphi}(z)}[logp(x^{i}, z)-logq_{\varphi}(z)]) \\ = & \nabla_{\varphi}\int_{z}q_{\varphi}(z)[logp(x^{i}, z) -logq_{\varphi}(z)]dz \\ = & \int_{z}\nabla_{\varphi}q_{\varphi}(z)[logp(x^{i}, z) - logq_{\varphi}(z)]dz \\ & +\int_{z}q_{\varphi}(z)\nabla_{\varphi}[logp(x^{i}, z)-logq_{\varphi}(z)]dz \\ = & A + B \end{aligned} ∇φL(φ)====∇φ(Eqφ(z)[logp(xi,z)−logqφ(z)])∇φ∫zqφ(z)[logp(xi,z)−logqφ(z)]dz∫z∇φqφ(z)[logp(xi,z)−logqφ(z)]dz+∫zqφ(z)∇φ[logp(xi,z)−logqφ(z)]dzA+B(3)
将(3)式第三行的两项分别记为 A 和 B A和B A和B,接下来分别求解。

所以最后 L ( φ ) 对 φ 的 导 数 L(\varphi)对\varphi的导数 L(φ)对φ的导数就可以用(4)式所示的期望来代替。这样我们就可以用蒙特卡洛模拟的方法,从 q φ ( z ) q_{\varphi}(z) qφ(z)中采样若干个点,然后来近似(4)式的期望,也就是近似 ∇ φ L ( φ ) \nabla_{\varphi}L(\varphi) ∇φL(φ)。这样就可以使用梯度下降的方法来更新 φ \varphi φ,最后求得 φ \varphi φ。
上面的方法看似可以,但是仔细分析会存在一些问题。(4)式是函数 ∇ φ l o g q φ ( z ) [ l o g p ( x i , z ) − l o g q φ ( z ) ] \nabla_{\varphi}logq_{\varphi}(z)[logp(x^{i}, z)-logq_{\varphi}(z)] ∇φlogqφ(z)[logp(xi,z)−logqφ(z)]在分布 q φ ( z ) q_{\varphi}(z) qφ(z)下的期望,但是 l o g q φ ( z ) logq_{\varphi}(z) logqφ(z)的梯度变化会非常大(log函数的图像是由陡变缓的)。假如采样了两个点 z 1 , z 2 , 但 是 q φ ( z 1 ) 接 近 0 , 而 q φ ( z 2 ) 接 近 1 z_{1}, z_{2},但是q_{\varphi}(z_{1})接近0,而q_{\varphi}(z_{2})接近1 z1,z2,但是qφ(z1)接近0,而qφ(z2)接近1,求导之后这两个点的梯度差是非常大的,所以会存在高方差的问题,高方差问题会导致在梯度更新时不稳定。所以就需要一种方法来降方差,使得梯度能稳定的更新。
重参数化降方差
关于重参数化技巧可以看苏剑林的科学空间漫谈重参数,讲解的很详细。下面贴一张从VAE中采样的图,帮助大家理解重参数。
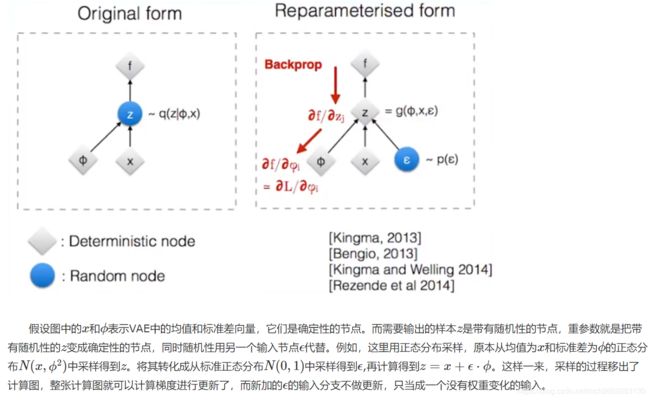
从(2)式可以看到,问题的根源是 z z z是从分布 q φ ( z ) q_{\varphi}(z) qφ(z)中采样得到的,所以将(2)式转化为积分形式后(如(3)式所示),里面会出现 q φ ( z ) q_{\varphi}(z) qφ(z),再对 φ \varphi φ求导就会变成(4)式,里面就会出现一项 ∇ φ l o g q φ ( z ) \nabla_{\varphi}logq_{\varphi}(z) ∇φlogqφ(z),这就会导致高方差的问题。
要是 z z z不从 q φ ( z ) q_{\varphi}(z) qφ(z)中直接采样,而是从一个已知的分布 p ( ε ) p(\varepsilon) p(ε)中采样得到 ε \varepsilon ε,再通过一个变换 z = g φ ( ε ) z=g_{\varphi}(\varepsilon) z=gφ(ε)得到 z z z,通过这样的过程来采样 z z z,将 z z z的随机性转化为 ε \varepsilon ε的随机性,这样就消除了高方差的问题。下面就通过公式来体验一下。
已知:
ε ∼ p ( ε ) , z = g φ ( ε ) \varepsilon \thicksim p(\varepsilon),z = g_{\varphi}(\varepsilon) ε∼p(ε),z=gφ(ε)。

通过推导我们得到了(6)式。在计算时,先从 p ( ε ) p(\varepsilon) p(ε)中采样出 ε 1 , , , ε k \varepsilon^{1}, ,,\varepsilon^{k} ε1,,,εk,对于某个 ε i \varepsilon^{i} εi,求出 ∇ z f ( z ) \nabla_{z}f(z) ∇zf(z), ∇ z f ( z ) \nabla_{z}f(z) ∇zf(z)中必定含有 z z z,再将 z = g φ ( ε i ) z=g_{\varphi}(\varepsilon^{i}) z=gφ(εi)带入计算,最后得到 ∇ z f ( z i ) ∇ φ g φ ( ε i ) \nabla_{z}f(z^{i})\nabla_{\varphi}g_{\varphi}(\varepsilon^{i}) ∇zf(zi)∇φgφ(εi),则
∇ φ L ( φ ) = 1 k ∑ i = 1 k ∇ z f ( z i ) ∇ φ g φ ( ε i ) φ ( t + 1 ) = φ ( t ) + λ ( t ) ∇ φ L ( φ ) \begin{aligned} \nabla_{\varphi}L(\varphi)= & {1 \over k} \sum_{i = 1}^{k} \nabla_{z}f(z^{i})\nabla_{\varphi}g_{\varphi}(\varepsilon^{i}) \\ \varphi^{(t+1)}=& \varphi^{(t)} + \lambda^{(t)}\nabla_{\varphi}L(\varphi) \end{aligned} ∇φL(φ)=φ(t+1)=k1i=1∑k∇zf(zi)∇φgφ(εi)φ(t)+λ(t)∇φL(φ)
通过上面的梯度更新,最后便可算出 φ \varphi φ,也就求得了分布 q φ ( z ) q_{\varphi}(z) qφ(z)。就可以用 q φ ( z ) 来 近 似 代 替 后 验 分 布 p ( z ∣ x ) q_{\varphi}(z)来近似代替后验分布p(z|x) qφ(z)来近似代替后验分布p(z∣x)。
参考:Gumbel-Softmax Trick和Gumbel分布
最后推荐苏剑林的科学空间中的有关博客和b站白板推导系列视频。