【图形与渲染】相机平面镜反射与斜裁剪矩阵(下)-斜裁剪矩阵
上一篇文章分析了平面镜反射效果实现中,如何计算镜像矩阵,我们已经可以得到镜像相机并渲染出镜像后的效果了,但是只是纯粹的镜像会遇到以下问题:
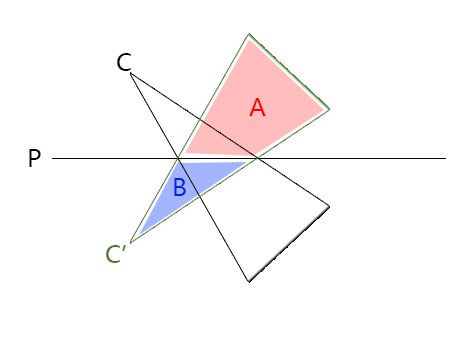
如图,当相机镜像到C’位置后,其视锥体裁剪范围是A+B,但实际应该位于反射贴图中的区域仅仅只有A区域,也就是我们需要根据平面P对相机C’裁剪。
投影矩阵:
先回顾一下渲染管线中的投影变换阶段,该阶段将相机空间的坐标变换到投影空间,以便于裁剪。
投影变换后会得到一个归一化设备坐标(NDC),其值在视锥体内的范围分别是x:[-1,1],y[-1,1],z:[-1,1](Direct3D中是[0,1],OpenGL中是[-1,1],unity采用了OpenGL的NDC)
投影矩阵可以通过相机的相关参数计算得到:
透视投影:
| 1/(tan(fov/2)*aspect) 0 0 0|
|0 1/tan(fov/2) 0 0|
|0 0 -(far+near)/(far-near) -2*near*far/(far-near)|
|0 0 -1 0|
正交投影:
|1/(aspect*size) 0 0 0|
|0 1/size 0 0|
|0 0 -2/(far-near) -(far+near)/(far-near)|
|0 0 0 1|
投影矩阵的详细推导可以参考相关文章,这里限于篇幅只给出具体的公式以方便下面的计算。
投影矩阵的推导:http://www.songho.ca/opengl/gl_projectionmatrix.html
近裁面和远裁面:
相机的视锥体由六个平面围成,其每个平面都可以用投影矩阵中的分量计算得到,但对于我们要实现的镜面反射效果,最重要的就是近裁面和远裁面,因此这里只考虑这两个平面。
根据投影变换的相关知识,实际上我们可以把投影空间看出一个”正方体”,它由六个面围成,
其中,近裁面为法线为(0,0,1),且过点(0,0,-1)的平面,则投影空间的近裁面P’near = <0,0,1,1>
远裁面为法线为(0,0,-1),且过点(0,0,1)的平面,则投影空间的远裁面P’far = <0,0,-1,1>
那么我们通过投影矩阵M即可求得相机空间对应的平面的表示,关于平面的变化可以参考:
http://www.lsngo.net/2018/01/07/graphics_plane/
因此,对于投影空间的平面L’,其相机空间对应的L即为:
![]()
即我们通过上述投影矩阵的转置矩阵可以求得相机空间的近裁面和远裁面,
最终计算结果,发现相机空间的近裁面和远裁面与投影矩阵刚好满足下列关系:
near = M4+M3
far = M4-M3
M4和M3表示矩阵M的第四行和第三行,这一步的结论对后序的推导十分重要。
替换近裁面:
有了以上基础知识后,我们就可以开始替换近裁面了,根据前面的实现,我们现在需要使用前面的平面P来替换近裁面,目前平面P是一个世界空间下的平面,我们需要先计算得到相机空间的平面Pc,由于近裁面near=M4+M3,因此替换近裁面后则有Pc=M4+M3。
通过对投影矩阵的推导可知投影矩阵的第四阶需要保持相机空间深度信息,且该阶需要对顶点透视校正插值,因此不可修改该阶的值,只能修改M3,即M3’=Pc-M4。
已知far=M4-M3,则替换近裁面后的远裁面far’=M4-M3’=M4-Pc+M4=2M4-Pc
但仅仅是这样求得新的远裁面far’并不一定能满足要求,大部分情况下,新的近裁面Pc和远裁面far’都不平行(只要Pc的x或y坐标有一个不为0),此时投影深度将不再表示延z坐标轴的距离,而仅仅只是新的近裁面和远裁面之间的一个点,这会对深度的精度产生影响。不过平面Pc中包含一个可以调节的比例系数,可以调整远裁面的方向,使得近裁面和远裁面不平行的情况下,近裁面和远裁面的夹角最小,且不对原始视锥进行裁剪。
修改远裁面:
far’=2M4-u*Pc
对于平面Pc,乘上比例系数u后,其表示的平面仍然是原平面。
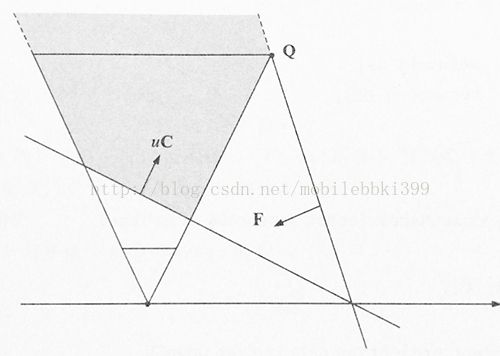
我们知道在投影空间中,远裁面上的四个角点的坐标分别是:(-1,-1,1,1),(-1,1,1,1),(1,-1,1,1),(1,1,1,1),为了使新的远裁面far’在不裁剪原视锥的同时又与近裁面夹角最小,其必须要经过一个离近裁面最远的角点,如下图:
此时的远裁面F经过离近裁面C最远的角点Q,这时的裁剪空间不会对原视锥进行裁剪,同时又使得夹角最小,
假设该点Q在投影空间对应的点为Q’,令Pc’为平面Pc在投影空间对应的平面,根据Pc’的法线可以计算得到点Q’的坐标为(sign(Pc’x),sign(Pc’y),1,1),(即和平面Pc’的法线同符号)
最后再利用投影矩阵M的逆矩阵计算得到相机空间的点Q,为了使远裁面far’包含Q,只需far’·Q=0,即可,
即far’ = 2M4-uPc
far’·Q=0,
最后得到u = (2*M4·Q)/(Pc·Q)
通过该u最终可以计算得到M3′
private Matrix4x4 ObliqueMatrix(Vector4 plane)
{
//世界空间的平面先变换到相机空间
plane = (m_MirrorCamera.worldToCameraMatrix.inverse).transpose * plane;
Matrix4x4 proj = m_MirrorCamera.projectionMatrix;
//计算近裁面的最远角点Q
Vector4 q = default(Vector4);
q.x = (Mathf.Sign(plane.x) + proj.m02) / proj.m00;
q.y = (Mathf.Sign(plane.y) + proj.m12) / proj.m11;
q.z = -1.0f;
q.w = (1.0f + proj.m22) / proj.m23;
Vector4 c = plane * (2.0f / Vector4.Dot(plane, q));
//计算M3'
proj.m20 = c.x;
proj.m21 = c.y;
proj.m22 = c.z + 1.0f;
proj.m23 = c.w;
return proj;
}最后渲染得到的RenderTexture传入shader,并在shader中计算投影坐标:
sampler2D _ReflTex;
half4 _Color;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.proj = ComputeGrabScreenPos(o.vertex);
return o;
}
fixed4 frag (v2f i) : SV_Target
{
fixed4 col = tex2Dproj(_ReflTex, i.proj);
col.rgb = lerp(col.rgb, _Color.rgb, 0.5);
return col;
}以上就是斜裁剪矩阵的推导。
最后,关于在unity引擎中实现斜裁剪,unity还提供了一个更方便的API,可以直接根据相机计算出斜裁剪矩阵:m_Camera.CalculateObliqueMatrix(clipPlane),可以直接使用这个API计算出斜裁剪矩阵,效果和上述方法是一样的。
更多内容请浏览我的博客原文:http://www.lsngo.net/2018/01/07/graphics_mirrorcamera_2/