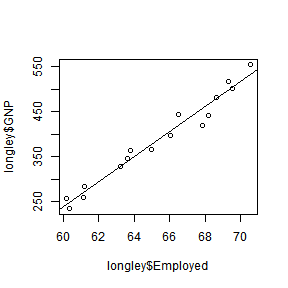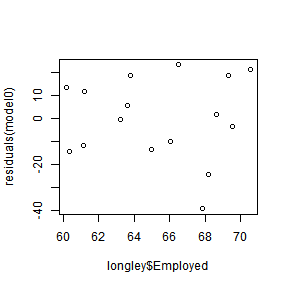统计与R入门: 回归分析
内容:
- 回归
- 零假说显著性检验
- 中央极限定理
- 抽样分布
- 一般线性模型
- 方差分析
- 调节
- 中介
- 路径模型
回归 (regression)
回归:用一个或多个预测变量(predictor)来预测结果变量(outcome variable)值的 统计 分析
- 简单回归:使用一个预测变量
- 多元回归:使用多个预测变量
简单回归的公式为:Y=B 0 +B 1 X 1 +e,其中:
- Y是X 1 的线性函数,是真实值
- m是回归常数(regression constant)(或称截距intercept)
- b是回归系数(regression coefficient)(或称斜率slope)
- e是误差(error)(或称残差residual)
实际使用时的回归模型是:Ŷ=B 0 +B 1 X 1 ,其中:
- Ŷ是预测值
评价回归模型,有如下两个较为重要的量:
- R多元回归系数(multiple correlation coefficient):即预测值与观测值之间的相关系数r ŶY
- R 2 :Y变量的偏差能被回归模型所能解释的程度
R和R 2 都是用来评价模型的总体表现的
- Y=B 0 +B 1 X 1 +B 2 X 2 +…+B K X K +e
R示例,使用longley数据集,数据集包含1947年至1962年16年的包含7个变量的经济数据。
head(longley)
## GNP.deflator GNP Unemployed Armed.Forces Population Year Employed ## 1947 83.0 234.3 235.6 159.0 107.6 1947 60.32 ## 1948 88.5 259.4 232.5 145.6 108.6 1948 61.12 ## 1949 88.2 258.1 368.2 161.6 109.8 1949 60.17 ## 1950 89.5 284.6 335.1 165.0 110.9 1950 61.19 ## 1951 96.2 329.0 209.9 309.9 112.1 1951 63.22 ## 1952 98.1 347.0 193.2 359.4 113.3 1952 63.64
plot(longley$Employed, longley$GNP) abline(lm(longley$GNP ~ longley$Employed))
尝试构建一个用就业人口预测国民生产总值的简单回归模型
用公式计算非标准化的回归系数、标准化的回归系数,以及运用coef函数和lm()函数计算回归系数
B <- cor(longley$Employed, longley$GNP) * sd(longley$GNP)/sd(longley$Employed) B
## [1] 27.84
model0 <- lm(longley$GNP ~ longley$Employed)
coef(model0)
## (Intercept) longley$Employed ## -1430.48 27.84
beta <- cor(longley$GNP, longley$Employed)
beta
## [1] 0.9836
计算多元回归系数R与R 2
R <- cor(longley$GNP, coef(model0)[1] + coef(model0)[2] * longley$Employed)
RSquared <- R^2
R
## [1] 0.9836
RSquared
## [1] 0.9674
R中可以用summary()来方便地获得这些量
summary(model0)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed) ## ## Residuals: ## Min 1Q Median 3Q Max ## -39.22 -11.92 0.85 14.88 23.56 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1430.48 89.36 -16.0 2.1e-10 *** ## longley$Employed 27.84 1.37 20.4 8.4e-12 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 18.6 on 14 degrees of freedom ## Multiple R-squared: 0.967, Adjusted R-squared: 0.965 ## F-statistic: 415 on 1 and 14 DF, p-value: 8.36e-12
回归系数的计算
选择回归系数的主要思想是:
- 选择能够使回归模型预测结果最佳的回归系数。
回归模型预测结果最佳,意味着残差(预测误差)最小。
残差e=Ŷ-Y,可能为正也可能为负,求平方和处理。
计算残差的平方和SS RESIDUAL =Σ(Ŷ-Y) 2 ,选择能够使这项最小的回归系数
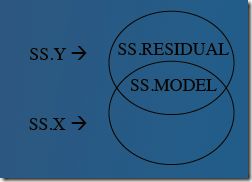
另一种考虑方式是,残差是模型所不能解释的偏差情况,用韦恩图加以解释:
- SS X 是变量X偏差的平方和SS X =Σ(X-M X ) 2
- SS Y 是变量Y偏差的平方和SS Y =Σ(Y-M Y ) 2
- SS MODEL =SP XŶ 是外积和即模型所能解释的偏差的平方和,SP XŶ = Σ[(X-MX )×(Ŷ-M Ŷ )]
- SS RESIDUAL 是模型所不能解释的残差的平方和SS RESIDUAL =Σ(Ŷ-Y) 2
选择能够使模型所不能解释的残差平方和最小的回归系数
非标准化的回归系数计算公式为:
- B 1 =r×(SD Y /SD X )
r是皮尔森积差相关系数,是变量Y随着变量X变化的程度,将其乘以Y与X的标准差之比,是考虑到Y与X的不同取值范围。
标准化的回归系数计算公式为:β=r
其原因是:经过标准化处理(均转换为Z值)的X与Y的标准差都为1。
线性回归的前提假设
线性回归的前提假设与相关性分析的前提假设基本一致:
- Y是正态分布
- X与Y之间是线性关系
- 方差齐性
- 变量X与Y的可靠性
- 变量X与Y的有效性
- 变量X与Y是否来自于随机抽样生成的具有代表性的样本
唯一的区别是,X不一定是正态分布的。
为了测试这些假设前提,通常可以绘制预测变量与残差的图表
回顾Anscombe’s quartet
par(mfrow = c(2, 2)) model1 <- lm(anscombe$y1 ~ anscombe$x1) plot(anscombe$x1, anscombe$y1, main = "1") abline(model1) model2 <- lm(anscombe$y2 ~ anscombe$x2) plot(anscombe$x2, anscombe$y2, main = "2") abline(model2) model3 <- lm(anscombe$y3 ~ anscombe$x3) plot(anscombe$x3, anscombe$y3, main = "3") abline(model3) model4 <- lm(anscombe$y4 ~ anscombe$x4) plot(anscombe$x4, anscombe$y4, main = "4") abline(model4)
计算残差,可以用公式计算,也可以调用predict()函数或者residuals()函数。
e1 <- anscombe$y1 - (coef(model1)[1] + coef(model1)[2] * anscombe$x1) e2 <- anscombe$y2 - (coef(model2)[1] + coef(model2)[2] * anscombe$x2) e3 <- anscombe$y3 - predict(model3) e4 <- residuals(model4)
par(mfrow = c(2, 2)) plot(anscombe$x1, e1, main = "1") plot(anscombe$x2, e2, main = "2") plot(anscombe$x3, e3, main = "3") plot(anscombe$x4, e4, main = "4")
只有左上方的满足方差齐性,残差与X无关,是随机的。
其他三个数据集都不满足线性回归分析的前提假设。
检验一下longley数据集中构建的线性回归模型
零假说显著性检验(Null Hypothesis Significance Testing,NHST)
- H 0 :零假说(Null Hypothesis)
- H A :对立假说(Alternative Hypothesis)
例如,相关性分析中,想证明两个变量之间不是无关的,运用零假说显著性检验,则:
- 零假说H 0 是:r=0
- 对立假说H A 是:r>0
- 零假说H 0 是:B=0
- 对立假说H A 是:B!=0
如果对立假说预测了X与Y之间的方向性,则称为:定向检验(directional test)或单尾检验(single tail test)=
否则称为无方向性检验(non-directional test),或双尾检验(two tail test)
考虑如下线性回归分析的显著性检验设定:
- 零假说H 0 是:B=0
- 对立假说H A 是:B!=0
假设H 0 为真,计算获得我们所拥有的数据的条件概率:
- p = P(D|H 0 )
如果发现该概率p值非常小,则驳回零假说,否则保留H 0 。
运用零假说显著性检验测试的可能结果如上图所示:
- 如果H 0 为真,显著性检验测试结果保留H 0 ,则检验结果是正确的
- 如果H 0 为假,显著性检验测试结果拒绝H 0 ,则检验结果是正确的
- 如果H 0 为真,显著性检验测试结果拒绝H 0 ,则是1型错误或称假警报(false alarm)
- 如果H 0 为假,显著性检验测试结果保留H 0 ,则是2型错误或称遗漏(miss)
- 正确的解读是:如果零假说是正确的,那么我们获得手头上数据或者更加极端数据的概率是p,即P(D|H 0 )
- 错误的解读是:零假说正确的概率是p,即即P(H 0 |D)
为了获得p值,需要首先计算出t值,公式为:
- B为非标准化的回归系数
- SE是的标准误差(standard error)是抽样 统计 量的标准差
对于回归系数而言,计算公式为:SE=SQRT[SS RESIDUAL /(DF)/SS X ]
t值是一个比例!
回归系数B是我们观测到的两个变量之间的线性相关程度
标准误差SE,是随机误差的情况
t值这个比例是:观测到的情况/随机情况,
如果t值为1,则说明观测到的情况与完全随机的情况是一样的
明显的t值越大,p值越小
中央极限定理部分再仔细解释t值。
R演示,计算以就业人数Employed预测国民生产总值GNP的回归系数的t值
此时SE计算公式为:SE=SQRT[(SS RESIDUAL /(N-2))/SS X ]
summary(model0)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed) ## ## Residuals: ## Min 1Q Median 3Q Max ## -39.22 -11.92 0.85 14.88 23.56 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1430.48 89.36 -16.0 2.1e-10 *** ## longley$Employed 27.84 1.37 20.4 8.4e-12 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 18.6 on 14 degrees of freedom ## Multiple R-squared: 0.967, Adjusted R-squared: 0.965 ## F-statistic: 415 on 1 and 14 DF, p-value: 8.36e-12
B <- coef(model0)[2] SSRESIDUAL <- sum((predict(model0) - longley$GNP)^2) NMinusP <- 16 - 2 SSX <- sum((longley$Employed - mean(longley$Employed))^2) SEReg <- sqrt((SSRESIDUAL/NMinusP)/SSX) tReg <- B/SEReg tReg
## longley$Employed ## 20.37
零假说显著性检验的问题和补救方法
零假说显著性检验的若干问题:
- 受到样本量的偏倚:样本量越大,t值越大,p值越小,越有可能拒绝零假说
- 随机选择的阀值α:即使是“标准”的阀值0.05的选择也是随机的
- 只知道NHST:有些情况下有比NHST更合适的显著性检验
- 容易产生误差:如果对同一个数据集做多个NHST容易产生1型错误,很多领域获得的数据的抽样误差较大,NHST容易产生2型错误
- 有问题的逻辑:NHST的逻辑是,如果假说成立,则不太可能获得当前数据(p->~q)。现在我们有这样的数据,因此假说不成立(q->~p)。
零假说显著性检验的补救方法:
- 受到样本量的偏倚:在NHST以外提供效应量(effect size)作为补充
- 随机选择的阀值α:提供效应量(effect size)作为补充,并且解读p值时,不按p值与α的距离汇报”高”显著性或”低”显著性
- 只知道NHST:学习其他假说检验方法,考虑模型比较(model comparison)
- 容易产生误差:重复试验以避免1型错误,获得随机的有代表性的样本以避免2型错误
- 有问题的逻辑:不要错误地解读p值
抽样分布 (sampling distributions)
如果知道样本数据的分布情况,我们可以做概率上的推理。
例如:知道人的体温是正态分布的,平均体温为36.5摄氏度。
那么随机选一个人测体温,其体温大于等于36.5摄氏度的概率是50%。
将其转换成Z值,即Z>0的概率为50%
体温大于38摄氏度,对应于Z值>2的概率为2%
抽样分布 的概念:
- 通过多个数据量相同的样本所获得的 统计 量的分布
- 平均值的抽样分布
- 相关性系数的抽样分布
- 回归系数的抽样分布
通常我们并没有多个样本,而只是估计抽样分布的情况。
- 假设我们有一个随机从总体中抽样出的样本量为N的样本
- 对这个样本,我们计算出平均值
- 假设我们现今有多个这样的随机样本,数据量均为N
- 这些样本的平均值一起构成了平均值的抽样分布
有了这样的平均值的抽样分布,我们可以回答这样的问题:
如果我们从总体中抽取一个样本,这个样本的平均值小于Z=0的概率是多少。
如果抽样分布是正态分布的,答案是0.5。
R演示,总体为1至50,每次抽取样本量为20的样本,4次实验分别抽取20次,100次,500次和2000次,分别绘制抽样平均值的柱图。
linearData <- c(1:50)
d <- c(20, 100, 500, 2000)
par(mfrow = c(2, 2))
set.seed(1)
for (i in 1:4) {
me <- vector()
for (j in 1:d[i]) {
me[j] <- mean(sample(linearData, 20))
}
hist(me)
}可以看出,无论总体分布情况如何,抽样次数越多,点统计量的抽样分布越接近于正态分布。
中央极限定律(central limit theorem)
- 抽样分布的平均值与总体的平均值相同
- 抽样分布的标准差是抽样分布方差的平方根,σ 2 =σ 2 /N
- 如果N>=30,或总体满足正态分布,则抽样分布的形状近似于正态分布
第三条告诉我们样本量足够大时,抽样分布的形状近似于正态分布。
t值也有一个抽样分布,称为t分布
t分布是一个分布族,不同的样本量大小对应不同的t分布,样本量越大t分布越接近正态分布
样本量越小,t分布越宽,达到同样大小的p值所需要的t值越大。
因此,在计算出t值后,根据样本量大小找出对应的t分布,在该分布上根据t值计算出p值。
将p值与0.05比较解读为:t值是否属于t分布中5%的极端情况中。
置信区间(confidence intervals)
任何一个样本统计量,如均值、标准差,都是点估计量(point estimates)。
即,一个样本平均值,代表的是平均值的抽样分布中的一个点。
置信区间是汇报一个可能值的区间估计(interval estimate),而非一个点估计量。置信区间是:根据随机样本,对总体参数所作出的一个区间估计。
例如:95%置信度意味着有95%的概率,区间中包含总体参数的真实值。
抽样误差将会导致不同的样本会有不同的点估计值
置信区间的优点是,将抽样误差考虑进来了,汇报的是区间估计
置信区间受到两方面的影响:
- 样本大小
- 总体和样本的方差大小
回顾平均值的标准误差为SE=SD/SQRT(N)很好解释了,置信区间与标准误差之间的关系。
- 上限M+t*SE
- 下限M+t*SE
t值取决于自由度(样本量决定)和置信度。
R示例,从国民生产总值中抽取一个样本量为10的样本,计算平均值,并汇报置信区间
set.seed(1)
S1 <- sample(longley$GNP, 10)
S1
## [1] 329.0 347.0 397.5 444.5 258.1 419.2 442.8 518.2 502.6 234.3
S1Mean <- mean(S1)
tcrit <- qt(c(0.025, 0.0975), df = 15)
S1SEMean <- sd(S1)/sqrt(16)
S1Mean + S1SEMean * tcrit
## [1] 338.1 356.7
回归系数的置信区间
回归系数B也是点估计量,从单一样本中获得的B值,是回归系数的抽样分布中的一个点。
回归系数的置信区间也是考虑进标准误差之后的结果。
置信度95解读为:有%95的概率,总体的回归系数在置信区间中。
R示例,用就业人数预测国民生产总值时回归系数的置信区间,confint()是简便算法。
tcrit <- qt(c(0.025, 0.0975), df = 14)
B + tcrit * SEReg
## [1] 24.91 25.98
confint(model0)
## 2.5 % 97.5 % ## (Intercept) -1622.14 -1238.82 ## longley$Employed 24.91 30.77
R示例,在图表上绘制回归系数的置信区间
library(ggplot2) ggplot(longley, aes(x = Employed, y = GNP)) + geom_smooth(method = "lm") + geom_point()
多元回归(multiple regression)
简单回归是只使用一个预测变量,多元回归是使用多个预测变量
公式为:Ŷ=B 0 +B 1 X 1 +B 2 X 2 +…+B K X K =Σ(B n X n )
- Ŷ是结果变量Y的预测值
- B 0 是在所有X均为0时的预测值
- X K 是预测变量
- B K 是非标准化的回归系数
- Y-Ŷ是残差(预测误差)
- K是预测变量的数量
同简单回归模型一样,评价多元回归模型,有如下两个较为重要的量:
- R多元回归系数(multiple correlation coefficient):即预测值与观测值之间的相关系数r ŶY
- R 2 :Y变量的偏差能被回归模型所能解释的程度
- R和R 2 都是用来评价模型的总体表现的
R示例,在longley数据集中,利用就业人数和总人口两个变量预测国民生产总值;
model5 <- lm(longley$GNP ~ longley$Employed + longley$Population) summary(model5)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed + longley$Population) ## ## Residuals: ## Min 1Q Median 3Q Max ## -11.689 -4.586 -0.695 3.858 14.241 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1372.095 36.141 -37.97 1.1e-14 *** ## longley$Employed 11.561 1.948 5.93 5.0e-05 *** ## longley$Population 8.556 0.984 8.70 8.8e-07 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 7.39 on 13 degrees of freedom ## Multiple R-squared: 0.995, Adjusted R-squared: 0.994 ## F-statistic: 1.35e+03 on 2 and 13 DF, p-value: 8.3e-16
betaEmployed <- coef(model5)[2]/sd(longley$GNP) * sd(longley$Employed) betaPopulation <- coef(model5)[3]/sd(longley$GNP) * sd(longley$Population) betaEmployed
## longley$Employed ## 0.4085
betaPopulation
## longley$Population ## 0.5988
通过p值发现,这两个变量均是显著的。比较标准化的回归系数,在这个多元回归模型中,相对于就业人数而言,人口是更强的预测变量。
多元回归的回归系数的估计
同简单回归一样,回归系数的值也是要是的模型的预测误差最小,即使残差的平方和最小。
标准化的多元回归模型公式(矩阵形式)为:Ŷ=B(X)
- Ŷ是N×1的向量
- B是K×1的向量
- X是N×K的矩阵
等式两边同时乘以X T 有:X T (Y)=X T (XB)
两边再同时乘以(X T X) -1 得到:B=(X T X) -1 (X T Y)
R示例,ginv()是矩阵求逆(inverse),需要MASS包裹,%*%是矩阵乘法,t()是矩阵转置(transpose)
library(MASS)
X <- data.matrix(longley[3:7])
Y <- data.matrix(longley[2])
B <- ginv(t(X) %*% X) %*% (t(X) %*% Y)
B
## GNP ## [1,] 0.007516 ## [2,] 0.087477 ## [3,] 9.518376 ## [4,] -0.713011 ## [5,] 9.773732
一般线性模型(general linear model,GLM)
一般线性模型是在许多常见的统计分析,例如多元回归和 方差分析 ( ANOVA )中采用的数学框架(mathematical framework)
- 线性的(linear):变量对之间假设是呈线性关系的
- 累加的(addictive):如果是用多个变量来预测一个结果变量,则每一个预测变量的效果都被认为是累加的
可以利用GLM来做一系列的检验,例如测试变量之间的非累加性质等。
下面举例说明一般线性模型的几种实例:
简单回归:Y=B 0 +B 1 X 1 +e,其中
- Y为薪水
- X 1 为工作年限
多元回归:Y=B 0 +B 1 X 1 +B 2 X 2 +B 3 X 3 +e,其中
- Y为薪水
- X 1 为工作年限
- X 2 为获奖次数
- X 3 为(工作年限*获奖次数)
X 3 是非累加的,加上这个变量可以用来测试获奖次数是否是 调节 变量,获奖次数是否能 调节 工作年限对薪水的影响。
单因素 方差分析 (one way ANOVA ): Y=B 0 +B 1 X 1 +e,其中
- Y为薪水
- X 1 为性别
在这个方差分析中,性别是类别变量,而非连续型变量。
因素方差分析(factorial ANOVA ):Y=B 0 +B 1 X 1 +B 2 X 2 +B 3 X 3 +e,其中
- Y为薪水
- X 1 为性别
- X 2 为民族
- X 3 为性别*民族
这个方差分析可以分析性别和民族之间的交互作用。
方差分析(Analysis of Variance,ANOVA)
是在因变量为类别变量而结果变量为连续变量时适用的分析方法。
方差分析最常用于有超过两个实验组时的随机实验所获得的数据
如果实验组只有2个,可以用非独立或独立t检验(indenpendent t-test, dependent t-test)
R示例,glm()函数,以npk数据集为例,做因素方差分析
head(npk)
## block N P K yield ## 1 1 0 1 1 49.5 ## 2 1 1 1 0 62.8 ## 3 1 0 0 0 46.8 ## 4 1 1 0 1 57.0 ## 5 2 1 0 0 59.8 ## 6 2 1 1 1 58.5
model6 <- glm(npk$yield ~ npk$N + npk$P + npk$K) summary(model6)
## ## Call: ## glm(formula = npk$yield ~ npk$N + npk$P + npk$K) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -9.267 -3.654 0.708 3.479 9.333 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 54.65 2.21 24.78 <2e-16 *** ## npk$N1 5.62 2.21 2.55 0.019 * ## npk$P1 -1.18 2.21 -0.54 0.597 ## npk$K1 -3.98 2.21 -1.81 0.086 . ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for gaussian family taken to be 29.17) ## ## Null deviance: 876.37 on 23 degrees of freedom ## Residual deviance: 583.48 on 20 degrees of freedom ## AIC: 154.7 ## ## Number of Fisher Scoring iterations: 2
虚拟编码(dummy coding)
虚拟编码是在回归分析中,将类别预测变量进行编码的系统。
- 因变量为:学科类别{人文社会科学,自然学科}
- 结果变量为:发文量
R示例,以iris数据集为例,对Species做虚拟编码处理,用以做回归分析,预测Sepal.Length。
演示两种dummy coding方法,C()和factor()
head(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species ## 1 5.1 3.5 1.4 0.2 setosa ## 2 4.9 3.0 1.4 0.2 setosa ## 3 4.7 3.2 1.3 0.2 setosa ## 4 4.6 3.1 1.5 0.2 setosa ## 5 5.0 3.6 1.4 0.2 setosa ## 6 5.4 3.9 1.7 0.4 setosa
spec.code <- C(iris$Species, treatment) model7 <- lm(iris$Sepal.Length ~ iris$Petal.Length + (spec.code)) summary(model7)
## ## Call: ## lm(formula = iris$Sepal.Length ~ iris$Petal.Length + (spec.code)) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.7531 -0.2314 -0.0008 0.2308 1.0310 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 3.6835 0.1061 34.72 < 2e-16 *** ## iris$Petal.Length 0.9046 0.0648 13.96 < 2e-16 *** ## spec.codeversicolor -1.6010 0.1935 -8.28 7.4e-14 *** ## spec.codevirginica -2.1177 0.2735 -7.74 1.5e-12 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.338 on 146 degrees of freedom ## Multiple R-squared: 0.837, Adjusted R-squared: 0.833 ## F-statistic: 249 on 3 and 146 DF, p-value: <2e-16
model7 <- lm(iris$Sepal.Length ~ iris$Petal.Length + factor(iris$Species)) summary(model7)
## ## Call: ## lm(formula = iris$Sepal.Length ~ iris$Petal.Length + factor(iris$Species)) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.7531 -0.2314 -0.0008 0.2308 1.0310 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 3.6835 0.1061 34.72 < 2e-16 *** ## iris$Petal.Length 0.9046 0.0648 13.96 < 2e-16 *** ## factor(iris$Species)versicolor -1.6010 0.1935 -8.28 7.4e-14 *** ## factor(iris$Species)virginica -2.1177 0.2735 -7.74 1.5e-12 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.338 on 146 degrees of freedom ## Multiple R-squared: 0.837, Adjusted R-squared: 0.833 ## F-statistic: 249 on 3 and 146 DF, p-value: <2e-16
调节(moderation)
也称交互作用(interaction)
一个调节变量(moderator variable)Z,能够加强回归模型,如果X与Y之间的关系是Z的函数。
以实验研究为例:通过调整自变量X,研究因变量Y的变化。
如果存在一个变量Z,并且发现X随着Y的变化情况随着Z的不同分布呈现出不一致的情况,则此时Z为调节变量
以相关性分析为例:假设X与Y之间存在相关性
存在调节变量Z意味着:X与Y之间的相关性对应于Z的分布呈现出不一致的情形。
即:在Z值不同的时候,X与Y之间的相关性不同
- 调节模型示例:假设X与Z均为连续型变量:
- Y=B 0 +B 1 X+B 2 Z+B 3 (X×Z)+e
假设X为类型变量,Z为连续变量,X有三种不同类型:
- Y=B 0 +B 1 (D1)+B 2 (D2)+B 3 (Z)+B 4 (D1×Z)+B 5 (D2×Z)+e
调节的检验:假设X与Z均为连续型变量,构建两个模型:
- Y=B 0 +B 1 X+B 2 Z+e
- Y=B 0 +B 1 X+B 2 Z+B 3 (X×Z)+e
假设X为类型变量,Z为连续变量,X有三种不同类型,构建两个模型:
- Y = B 0 +B 1 (D1)+B 2 (D2)+B 3 Z+e
- Y=B 0 +B 1 (D1)+B 2 (D2)+B 3 (Z)+B 4 (D1×Z)+B 5 (D2×Z)+e
- 比较R 2 的值
- 评价与调节效应有关的预测变量的回归系数,如(X×Z),(D1×Z),(D1×Z)对应的回归系数
model00 <- lm(longley$GNP ~ longley$Employed + longley$Unemployed) model01 <- lm(longley$GNP ~ longley$Employed + longley$Unemployed + (longley$Employed * longley$Unemployed)) summary(model00)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed + longley$Unemployed) ## ## Residuals: ## Min 1Q Median 3Q Max ## -28.092 -6.154 0.062 7.498 22.245 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1.34e+03 7.01e+01 -19.16 6.5e-11 *** ## longley$Employed 2.57e+01 1.16e+00 22.12 1.1e-11 *** ## longley$Unemployed 1.57e-01 4.37e-02 3.58 0.0034 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 13.7 on 13 degrees of freedom ## Multiple R-squared: 0.984, Adjusted R-squared: 0.981 ## F-statistic: 389 on 2 and 13 DF, p-value: 2.52e-12
summary(model01)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed + longley$Unemployed + ## (longley$Employed * longley$Unemployed)) ## ## Residuals: ## Min 1Q Median 3Q Max ## -23.423 -7.784 0.028 8.694 20.475 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -988.7175 340.7291 -2.90 0.0133 ## longley$Employed 20.2828 5.2582 3.86 0.0023 ## longley$Unemployed -0.9030 0.9963 -0.91 0.3826 ## longley$Employed:longley$Unemployed 0.0162 0.0152 1.06 0.3080 ## ## (Intercept) * ## longley$Employed ** ## longley$Unemployed ## longley$Employed:longley$Unemployed ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 13.6 on 12 degrees of freedom ## Multiple R-squared: 0.985, Adjusted R-squared: 0.981 ## F-statistic: 262 on 3 and 12 DF, p-value: 3.34e-11
anova(model00, model01)
## Analysis of Variance Table ## ## Model 1: longley$GNP ~ longley$Employed + longley$Unemployed ## Model 2: longley$GNP ~ longley$Employed + longley$Unemployed + (longley$Employed * ## longley$Unemployed) ## Res.Df RSS Df Sum of Sq F Pr(>F) ## 1 13 2435 ## 2 12 2225 1 210 1.13 0.31
预测变量的中心化(centralization)
中心化处理是对变量值进行转变,转变为以0为均值
公式为:X=X-M X
- 如果所有的预测变量取0时都无意义,则截距/回归常数B 0 的解读是无意义的
- 如果不存在调节效应,无论Z的取值,B 1 的取值是稳定的
- 如果存在调节效应,Z的取值不同,B 1 的取值是变化的
-
避免多元共线性(multicolinearity),如果一般线性模型中的两个变量之间相关性很高,则两者是冗余的,预测两者分别对应的回归系数会很困难
中介 (mediation)
中介 分析(mediation analysis)被用来更好地理解观测到的自变量对因变量的影响,或者X与Y之间的相关性
如果X与Y是相关的,但是有中介变量M在其中起作用(X->M->Y),意味着:
- Y=B 0 +B 1 M+e
- M=B 0 +B 1 X+e
- Y=B 0 +B 1 M+B 2 X+e
我们可以看回归系数B 2 是否显著。如果一个中介变量M对X与Y之间的关系起到作用,则可分为:
- 起到部分作用:部分中介
- 起到全部作用:完全中介
- lm(Y~X)
- lm(M~X)
- lm(Y~X+M)
- lm(Y~X)中X的回归系数应该显著
- lm(M~X)中X的回归系数应该显著
- lm(Y~X+M)中M的回归系数显著,看X的回归系数如何
model11 <- lm(longley$GNP ~ longley$Employed) model12 <- lm(longley$Population ~ longley$Employed) model13 <- lm(longley$GNP ~ longley$Employed + longley$Population) summary(model11)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed) ## ## Residuals: ## Min 1Q Median 3Q Max ## -39.22 -11.92 0.85 14.88 23.56 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1430.48 89.36 -16.0 2.1e-10 *** ## longley$Employed 27.84 1.37 20.4 8.4e-12 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 18.6 on 14 degrees of freedom ## Multiple R-squared: 0.967, Adjusted R-squared: 0.965 ## F-statistic: 415 on 1 and 14 DF, p-value: 8.36e-12
summary(model12)
## ## Call: ## lm(formula = longley$Population ~ longley$Employed) ## ## Residuals: ## Min 1Q Median 3Q Max ## -3.522 -1.364 -0.362 1.851 2.792 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -6.824 9.648 -0.71 0.49 ## longley$Employed 1.902 0.148 12.90 3.7e-09 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 2.01 on 14 degrees of freedom ## Multiple R-squared: 0.922, Adjusted R-squared: 0.917 ## F-statistic: 166 on 1 and 14 DF, p-value: 3.69e-09
summary(model13)
## ## Call: ## lm(formula = longley$GNP ~ longley$Employed + longley$Population) ## ## Residuals: ## Min 1Q Median 3Q Max ## -11.689 -4.586 -0.695 3.858 14.241 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1372.095 36.141 -37.97 1.1e-14 *** ## longley$Employed 11.561 1.948 5.93 5.0e-05 *** ## longley$Population 8.556 0.984 8.70 8.8e-07 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 7.39 on 13 degrees of freedom ## Multiple R-squared: 0.995, Adjusted R-squared: 0.994 ## F-statistic: 1.35e+03 on 2 and 13 DF, p-value: 8.3e-16
路径模型(path model)
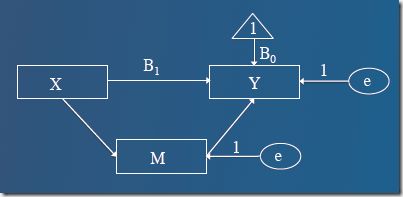
中介分析通常使用路径模型来分析,其中:
- 矩形代表观测到的变量(X,Y,M)
- 圆圈代表未观测到的变量(误差e)
- 三角代表常量
- 箭头代表关系
Sobel检验中z值的计算公式:
z=(B a *B b )/SQRT[(B a 2 *SE b 2 )+(B b 2 *SE a 2 )]
library(multilevel)
## Loading required package: nlme
sobel(longley$Employed, longley$Population, longley$GNP)
## $`Mod1: Y~X` ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1430.48 89.361 -16.01 2.146e-10 ## pred 27.84 1.366 20.37 8.363e-12 ## ## $`Mod2: Y~X+M` ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1372.095 36.1406 -37.965 1.051e-14 ## pred 11.561 1.9484 5.933 4.958e-05 ## med 8.556 0.9837 8.698 8.850e-07 ## ## $`Mod3: M~X` ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -6.824 9.6480 -0.7073 4.910e-01 ## pred 1.902 0.1475 12.8956 3.693e-09 ## ## $Indirect.Effect ## [1] 16.28 ## ## $SE ## [1] 2.257 ## ## $z.value ## [1] 7.211 ## ## $N ## [1] 16