算法与数据结构学习笔记-字符串之最长公共子序列,LCS问题的动态规划解法
问题:给定两个字符串,找出它们的最长公共子序列。
首先了解题目,子序列和字串是不同的。在字符串匹配里,子串通常指的是给定字符串的一部分,是连续的不可断开的。而子序列是不同的,是在给定字符串里,按照顺序取字符,可以连续可以断开,然后组合构成新的字符串。通常子序列都不是给定字符串的子串,但是子串也可以称为子序列。另外公共子序列不一定是最长公共子序列的子串。
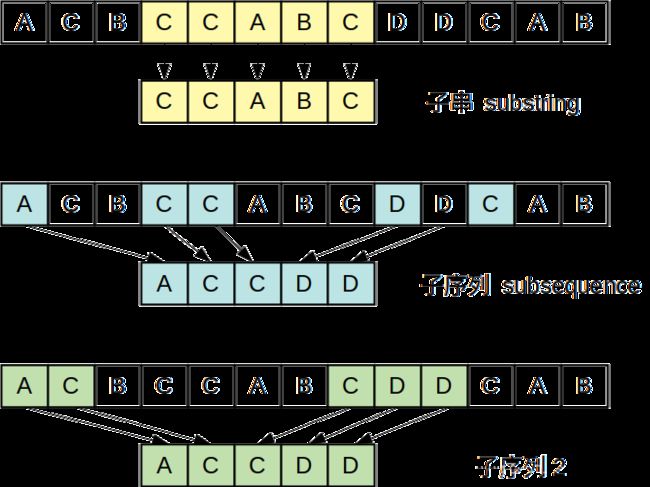
不同的取字符方式可以构建出相同的子序列,如上图子序列和子序列2。而当给定两个字符串,公共子序列代表可以从两个字符串里按顺序抽取字符并组成新的序列,且新的序列相同,最长公共子序列则代表能用这种方式取出最长的相同序列。
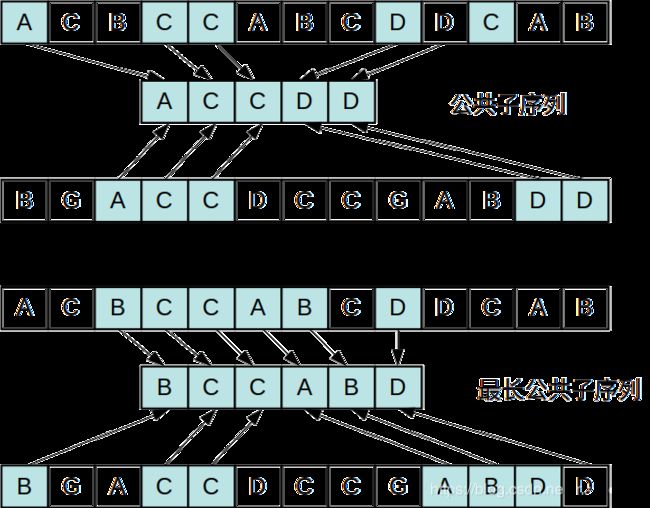
生物学上的DNA匹配其实就是在寻找最长公共子序列。比如 S 1 = A C C G G A T C C G , S 2 = C C G A T C G C G C C G S_1=ACCGGATCCG, S_2=CCGATCGCGCCG S1=ACCGGATCCG,S2=CCGATCGCGCCG,可以找到它们的最长公共子序列为 C C G A T C C G CCGATCCG CCGATCCG。如果用暴力解法来解决这个问题,需要对检查两条字符串的所有子序列,效率很低。如果想找到更快的解法,需要研究一下公共子序列的性质,即它与两条给定字符串有什么关系,为了方便,称给定字符串为X和Y,它们的最长公共子序列为Z。
- 如果X和Y的最后一个元素相同,那么它们的最后一个元素也是Z的最后一个元素。若将X,Y和Z的最后一个元素全部去掉,得到X’,Y’,Z’,Z’依旧是X’和Y’的最长公共子序列。
- 如果X和Y的最后一个元素不同,如果Z的最后一个元素和X的最后一个元素不同,那么把X的最后一个元素去掉得到X’,那么Z依旧是X’和Y的最长公共子序列。
- 如果X和Y的最后一个元素不同,如果Z的最后一个元素和Y的最后一个元素不同,那么把Y的最后一个元素去掉得到Y’,那么Z依旧是X和Y‘的最长公共子序列。
这几条性质比较好理解。其中2和3是对称的。如果一个给定字符串里的最后一个元素不能放在公共子序列里, 那么这个字符串的搜索范围可以缩小,这也是用动态规划解这道题的部分基础:如果X和Y的最末元素相同,那么子问题是在X’和Y’里查找最长公共子序列(找到后需要将最末公共元素加上); 如果X和Y的最末元素不同,则产生了两个子问题:1. 查找X’和Y的最长公共子序列。2. 查找X和Y’的最长公共子序列(找到后需要比较两个子序列并取最长)。
用递归公式来表示如下:
c [ i , j ] = { 0 i = 0 或 j = 0 c [ i − 1 , j − 1 ] + 1 i , j > 0 且 x i = y i m a x ( c [ i , j − 1 ] , c [ i − 1 , j ] ) i , j > 0 且 x i ≠ y i . c[i,j]= \begin{cases} 0 & & {i=0 或 j=0}\\ c[i-1,j-1]+1 & & {i, j>0 且 x_i=y_i}\\ max(c[i,j-1], c[i-1,j]) & & {i, j>0 且 x_i\neq y_i} \end{cases} . c[i,j]=⎩⎪⎨⎪⎧0c[i−1,j−1]+1max(c[i,j−1],c[i−1,j])i=0或j=0i,j>0且xi=yii,j>0且xi=yi.
我们使用自下而上的动态规划法,使用一个表格c来记录对所有i和j得到的最长公共子序列的长度(记录已经计算过的数据是动态规划的基本思想,否则一般的递归会对很多相同问题重复计算)。如果要求最后不仅仅获得最优解的长度,且要输出解,那么还需要另外记录其它信息,以便输出找到的最长公共子序列。我们先看一下另一个表格可能的模样:
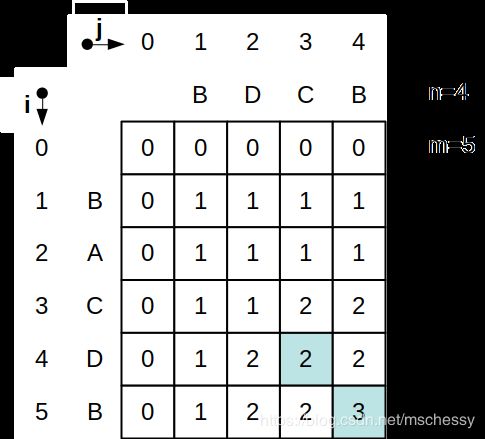
给定的两个序列分别是 X = B A C D B , Y = B D C B X=BACDB,Y=BDCB X=BACDB,Y=BDCB,其中 n = 5 , m = 4 n=5,m=4 n=5,m=4。假设搜索到 i = 4 , j = 3 i=4,j=3 i=4,j=3时,发现 X i + 1 = Y j + 1 ( X 5 = Y 4 ) X_{i+1}=Y_{j+1}(X_5=Y_4) Xi+1=Yj+1(X5=Y4),那么确定地,如果 c [ 4 ] [ 3 ] c[4][3] c[4][3]在Z里, c [ 5 ] [ 4 ] c[5][4] c[5][4]也会加到Z上,且在 c [ 4 ] [ 3 ] c[4][3] c[4][3]后面。如果发现 X i + 1 ≠ Y j + 1 X_{i+1}\neq Y_{j+1} Xi+1=Yj+1,则要比较 c [ i ] [ j + 1 ] c[i][j+1] c[i][j+1]和 c [ i + 1 ] [ j ] c[i+1][j] c[i+1][j],取较大的并沿着该方向搜索。如果 c [ i ] [ j + 1 ] = c [ i + 1 ] [ j ] c[i][j+1]=c[i+1][j] c[i][j+1]=c[i+1][j],取其中一个方向就好了。
所以我们可以在表格上加一些标记,记录三种情况: X i = Y j X_i=Y_j Xi=Yj, X i ≠ Y j X_i\neq Y_j Xi=Yj但 c [ i ] [ j − 1 ] ≥ c [ i − 1 ] [ j ] c[i][j-1]\geq c[i-1][j] c[i][j−1]≥c[i−1][j], X i ≠ Y j X_i\neq Y_j Xi=Yj但 c [ i ] [ j − 1 ] < c [ i − 1 ] [ j ] c[i][j-1]
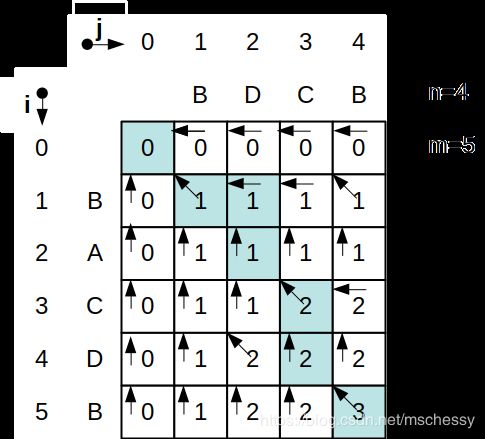
根据箭头检索,能输出符合条件的序列,注意只有 ↖ \nwarrow ↖的值会被输出。为了方便,可以先反向地看。找到表中的最大值3,此时 i = 5 , j = 4 i=5,j=4 i=5,j=4,发现是 ↖ \nwarrow ↖,输出该值,看箭头指的下一个值, i = 4 , j = 3 i=4,j=3 i=4,j=3,发现 ↑ \uparrow ↑,按箭头指向继续查找,找到 i = 3 , j = 3 i=3,j=3 i=3,j=3,是 ↖ \nwarrow ↖,输出该值。下一次查看 i = 2 , j = 2 i=2,j=2 i=2,j=2,按照箭头 i = 1 , j = 2 i=1,j=2 i=1,j=2; i = 1 , j = 1 i=1,j=1 i=1,j=1,发现是 ↖ \nwarrow ↖,输出并结束。此时我们得到BCB这个序列。我们此时是从后往前的检索,得到的序列是反的。虽然这道题结果相同,但实际输出的时候要反过来,如按照这种方式得到了ABCD序列,输出时应该是DCBA。
#include