CV笔记9:纹理特征之LBP特征(基于python实现)
目录
- 一、背景介绍
- 1.1 什么是纹理特征?
- 1.2 纹理描述方法
- 二、基于python的LBP算法说明及实现
- 2.1 LBP特征提取的一般步骤
- 2.2 原始LBP
- 2.3 圆形LBP算子
- 2.5 旋转不变性
- 2.4 等价模式和混合模式
- 三、基于python-skimage的LBP实现
- 四、基于python-opencv的LBP实现
- 参考
一、背景介绍
LBP特征曾广泛应用在人脸检测中,但随着深度学习的发展,其竞争力有所下降,但却不能抹灭其存在的价值意义。LBP特征是一种用来描述图像局部纹理的特征描述子,具有旋转不变性、灰度不变性等有点,虽然原理简单但效果非凡。
1.1 什么是纹理特征?
人们对纹理的感受是与心理效果相结合的,所以用语言和文字来描述是有一定困难的。我们先给出简单的描述:纹理是一种反映图像中同质现象的视觉特征,它体现了物体表面的具有缓慢变化或者周期性变化的表面结构组织排列属性。
纹理具有三大标志:
- 某种局部序列性不断重复;
- 非随机排列;
- 纹理区域内大致为均匀的统一体;
什么意思呢?我们来看图片:

细品,纹理是不是能够体现出不同物体表面的固有属性?虽然表面看似没有规律,但又含有内在的规律。所以,纹理特征有助于将两种不同的物体(或者两幅图像)区别开来,比如树叶的纹理和建筑物的纹理就会有很大的区别。进一步的我们还应该从下面两个角度去理解纹理:
- 纹理与尺度有密切联系,一般仅在一定的尺度上可以观察到,对纹理的分析也需要在恰当的尺度上进行。例如,在给定的一幅图像中,当在较粗的尺度上观察时可能看不出纹理,可能需要到更细的尺度上才能观察的到。任何物体的表面,如果一直放大下去进行观察的话一定能够显现出纹理。
- 同时,纹理也具有区域性的特点,通常被看作对局部区域中像素之间关系的一种度量,对单个的像素来说是没有纹理概念的。纹理能用来描述不同的图像区域,要描述一个图像中的纹理区域,常会使用区域的尺寸、可分辨灰度元素的数目以及这些灰度元素的相互关系等。
1.2 纹理描述方法
纹理分析其实是一门很深的学问,对纹理的描述也有多种方法:统计方法、结构方法、频谱方法等,此处就不再多做叙述,可以参见文章《图像纹理特征总体简述》。而对于LBP特征描述子就是结构方法中的一种,是一种借助局部邻域定义的纹理测度。本文也重点讲述LBP特征描述子。
二、基于python的LBP算法说明及实现
2.1 LBP特征提取的一般步骤
- 将检测窗口划分为16*16的小区域(cell)
- 对于每个cell中的一个像素,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0.这样, 3 × 3 3×3 3×3邻域内的8个点经过比较可产生8位二进制数,即得到该窗口中心像素点的LBP值;
- 计算每个cell的直方图,即每个数字出现的频率,然后对该直方图进行归一化处理
- 最后将得到的每个cell的统计直方图进行连接成一个特征向量,也就是整幅图的LBP纹理特征向量
2.2 原始LBP
原始的LBP算子简单讲就是在像素 3 × 3 3×3 3×3的邻域内,以邻域中心像素为阈值,相邻的8个像素的灰度值分别与邻域中心的像素值做比较,若周围像素大于中心像素值,则该像素点的位置被标记为1,否则为0,如下面的图片描述。这样, 3 × 3 3×3 3×3邻域内的8个点经过比较可产生8为二进制数,将这8位二进制数按一定次序排列成一个二进制数字,这个二进制数字就是中心像素的LBP值,可以看出LBP值共有 2 8 2^8 28种可能。因此,中心像素的LBP值也就反映了该像素周围区域的纹理信息。

再严谨一点,我们使用公式进行表示:
在LBP特征表达中,可以用图像的局部领域的联合分布 T T T 来描述图像的纹理特征。假设局部邻域中像素个数为 P ( P > 1 ) P(P >1) P(P>1),那么纹理特征的联合分布 T T T 可以表述成:
T = t ( g c , g 0 , … , g p − 1 ) p = 0 , … , P − 1 (2-1) T=t\left(g_{c}, g_{0}, \ldots, g_{p-1}\right) \quad p=0, \ldots, P-1\tag{2-1} T=t(gc,g0,…,gp−1)p=0,…,P−1(2-1)其中, g c g_c gc 表示相应局部邻域的中心像素的灰度值, g p g_p gp 表示以中心像素圆心,以R为半径的圆上的像素的灰度值。
假设中心像素和局部邻域像素相互独立,那么这里可以将上面定义式写成如下形式:
T = t ( g c , g 0 − g c , … , g p − 1 − g c ) p = 0 , … , P − 1 ≈ t ( g c ) t ( g 0 − g c , … , g p − 1 − g c ) (2-2) \begin{aligned} T &=t\left(g_{c}, g_{0}-g_{c}, \ldots, g_{p-1}-g_{c}\right) \quad p=0, \ldots, P-1 \\ & \approx t\left(g_{c}\right) t\left(g_{0}-g_{c}, \ldots, g_{p-1}-g_{c}\right) \end{aligned}\tag{2-2} T=t(gc,g0−gc,…,gp−1−gc)p=0,…,P−1≈t(gc)t(g0−gc,…,gp−1−gc)(2-2)其中 t ( g c ) t(g_c) t(gc)决定了局部区域的整体亮度,对于纹理特征,可以忽略这一项,最终得到:
T ≈ t ( g 0 − g c , … , g p − 1 − g c ) p = 0 , … , P − 1 (2-3) T \approx t\left(g_{0}-g_{c}, \ldots, g_{p-1}-g_{c}\right) \quad p=0, \ldots, P-1\tag{2-3} T≈t(g0−gc,…,gp−1−gc)p=0,…,P−1(2-3)上式说明,将纹理特征定义为邻域像素和中心像素的差的联合分布函数,因为 g p − g c g_p − g_c gp−gc是基本不受亮度均值影响的,所以从上式可以看出,此时统计量T 是一个跟亮度均值,即灰度级无关的值。
最后定义特征函数如下:
T ≈ t ( s ( g 0 − g c ) , … , s ( g p − 1 − g c ) ) p = 0 , … , P − 1 s ( x ) = { 1 , x ≥ 0 0 , x < 0 (2-4) \begin{array}{l} T \approx t\left(s\left(g_{0}-g_{c}\right), \ldots, s\left(g_{p-1}-g_{c}\right)\right) \quad p=0, \ldots, P-1 \quad s(x)=\left \{ \begin{matrix} 1, x \geq 0 \\ 0, x<0 \end{matrix}\right. \end{array}\tag{2-4} T≈t(s(g0−gc),…,s(gp−1−gc))p=0,…,P−1s(x)={1,x≥00,x<0(2-4)定义灰度级不变LBP为:
L B P P , R = ∑ p = 0 P − 1 s ( g p − g c ) 2 p (2-5) L B P_{P, R}=\sum_{p=0}^{P-1} s\left(g_{p}-g_{c}\right) 2^{p}\tag{2-5} LBPP,R=p=0∑P−1s(gp−gc)2p(2-5)即二进制编码公式。
代码实现
def lbp(src):
'''
:param src:灰度图像
:return:lbp特征
'''
height, width = src.shape[:2]
dst = np.zeros((height, width), dtype=np.uint8)
lbp_value = np.zeros((1,8), dtype=np.uint8)
neighbours = np.zeros((1,8), dtype=np.uint8)
for row in range(1, height-1):
for col in range(1, width-1):
center = src[row, col]
neighbours[0, 0] = src[row-1, col-1]
neighbours[0, 1] = src[row-1, col]
neighbours[0, 2] = src[row-1, col+1]
neighbours[0, 3] = src[row, col+1]
neighbours[0, 4] = src[row+1, col+1]
neighbours[0, 5] = src[row+1, col]
neighbours[0, 6] = src[row+1, col-1]
neighbours[0, 7] = src[row, col-1]
for i in range(8):
if neighbours[0, i] > center:
lbp_value[0, i] = 1
else:
lbp_value[0, i] = 0
# 转成二进制数
lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
+ lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 7] * 128
dst[row, col] = lbp
return dst
2.3 圆形LBP算子
原始的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征,并达到灰度级和旋转不变性的要求,Ojala等对 LBP算子进行了改进,将 3×3邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP算子允许在半径为 R的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子,表示为 L B P P R LBP^{R}_P LBPPR;
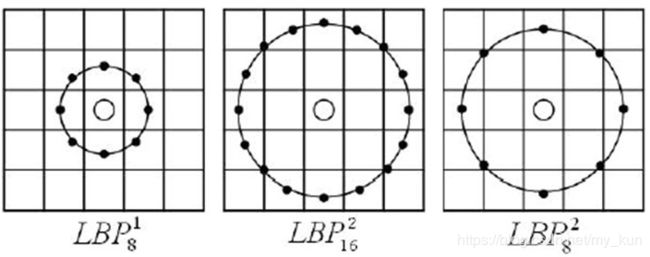
对于给定中心点 ( x c , y c ) (x_c,y_c) (xc,yc),其邻域像素位置为 ( x p , y p ) (x_p,y_p) (xp,yp), p ∈ P p∈P p∈P,其采样点 ( x p , y p ) (x_p,y_p) (xp,yp)用如下公式计算:
x p = x c + R×cos ( 2 π p P ) y p = y c + R×sin ( 2 π p P ) (2-6) \begin{array}{l} x_{p}=x_{c}+\operatorname{R×cos}\left(\frac{2 \pi p}{P}\right) \\ \\ y_{p}=y_{c}+\operatorname{R×sin}\left(\frac{2 \pi p}{P}\right) \end{array}\tag{2-6} xp=xc+R×cos(P2πp)yp=yc+R×sin(P2πp)(2-6)R是采样半径,p是第p个采样点,P是采样数目。如果近邻点不在整数位置上,就需要进行插值运算,一般可以使用双线性插值法来计算该点的像素值。
2.5 旋转不变性
从原始LBP的定义来看,LBP算子是灰度不变的,但不是旋转不变的。图像旋转的话就会得到不同的LBP值。可对原始LBP算子进行了扩展,不断旋转圆形邻域得到一系列初始定义的 LBP值,取其最小值作为该邻域的 LBP 值,即具有旋转不变性的 LBP 算子。
实现方法:不断旋转圆形邻域得到一系列初始定义的LPB值,取最小值作为该邻域的值。
L B P P R r i = min ( R O R ( L B P P , R r i , i ) ∣ i = 0 , 1 , … , P − 1 ) (2-7) L B P_{P R}^{ri}=\min \left(R O R\left(L B P_{P, R}^{ri}, i\right) | i=0,1, \ldots, P-1\right)\tag{2-7} LBPPRri=min(ROR(LBPP,Rri,i)∣i=0,1,…,P−1)(2-7)其中 L B P P R r i L B P_{P R}^{ri} LBPPRri表示具有旋转不变性的LBP特征。 R O R ( x , i ) ROR(x, i) ROR(x,i)为旋转函数,表示将 x x x右循环 i i i位。
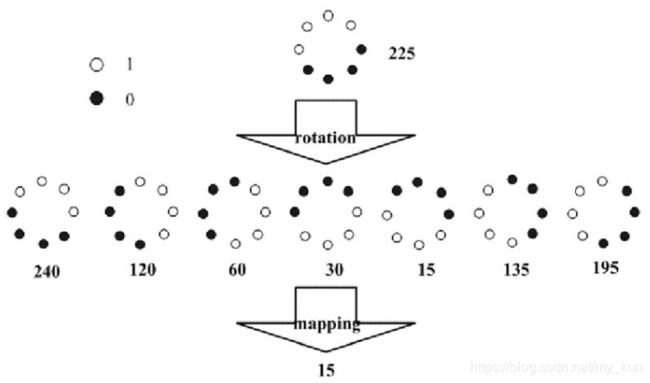
从上图中可以进一步解释,原始LBP得到的数值转化为二进制编码,对它进行循环移位操作,有8种情况(包括自身)。取其中最小的一个值,比如图中就对应着15,这个值是旋转不变的,因为对图像做旋转操作等价与上面8种移位的过程,而8种情况都对应同一个值,即8个值中的最小值15,即拥有了旋转不变特性。
2.4 等价模式和混合模式
一个LBP算子可以产生不同的二进制模式,对于半径为R的圆形区域内含有 p p p个采样点的LBP算子将会产生 2 p 2^p 2p种模式。很显然,随着邻域集内采样点数的增加,二进制模式的种类是急剧增加的。例如: 5 × 5 5×5 5×5邻域内20个采样点,有 2 20 = 1 , 048 , 576 2^{20}=1,048,576 220=1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时,过多的模式种类对于纹理的表达是不利的。
为了解决二进制模式过多的问题,提高统计性,Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。Ojala等认为,在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变),00000111(只含一次从0到1的跳变),10001111(先由1跳到0,再由0跳到1,共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共四次跳变)。
通过这样的改进,二进制模式的种类大大减少,而不会丢失任何信息。模式数量由原来的 2 p 2^p 2p种减少为 p ( p − 1 ) + 2 p( p-1)+2 p(p−1)+2种,其中 p p p表示邻域集内的采样点数。对于3×3邻域内8个采样点来说,二进制模式由原始的256种减少为58种,这使得特征向量的维数更少,并且可以减少高频噪声带来的影响。
关于 p ( p − 1 ) + 2 p( p-1)+2 p(p−1)+2的推导:
假设在某一邻域的采样点个数为 p p p,分别对跳变次数为0、1、2的二进制数进行求解:
0次跳变: 意味着二进制数的每一位上都相同,所以全为0或1,则存在2种可能;
1次跳变: 意味着二进制数可以分成2段看待,其前半段和后半段保持不同,如11110000,00000011,则存在 2 × ( p − 1 ) 2×(p-1) 2×(p−1)种可能;
2次跳变: 意味着二进制数可以分成3段看待前段、中间段和后端,其前段和后段要保持数值一致,中间段与其不同,如11000001,00010000,则存在 2 × ( p − 2 ) × ( p − 3 ) × ( p − 4 ) × ⋯ × 1 = ( p − 2 ) + ( p − 2 ) 2 2×(p-2)×(p-3) ×(p-4)×\dots ×1 = (p-2)+(p-2)^2 2×(p−2)×(p−3)×(p−4)×⋯×1=(p−2)+(p−2)2种可能;
将以上三种相加合并化简可以得到 p ( p − 1 ) + 2 p( p-1)+2 p(p−1)+2种模式。
检查某种模式是否是等价模式:
U ( G p ) = ∣ s ( g p − 1 − g c ) − s ( g 0 − g c ) ∣ + ∑ p = 1 P − 1 ∣ s ( g p − g c ) − s ( g P − 1 − g c ) ∣ (2-8) U\left(G_{p}\right)=\left|s\left(g_{p_{-1}}-g_{c}\right)-s\left(g_{0}-g_{c}\right)\right|+\sum_{p=1}^{P_{-1}}\left|s\left(g_{p}-g_{c}\right)-s\left(g_{P-1}-g_{c}\right)\right|\tag{2-8} U(Gp)=∣s(gp−1−gc)−s(g0−gc)∣+p=1∑P−1∣s(gp−gc)−s(gP−1−gc)∣(2-8)将其和其移动一位后的二进制模式按位相减。并绝对值求和。若U ( G p ) \left(G_{p}\right) (Gp) 小于等于2,则为等价模式。
三、基于python-skimage的LBP实现
在skimage包中提供了LBP算法,可以很简单的实现LBP特征提取功能,并且提供了原始LBP、灰度旋转不变的LBP、均匀模式的LBP等多种实现方法。
skimage.feature.local_binary_pattern(image, P, R, method=‘default’)
Parameters
image:(N, M) array
Graylevel image.
P: int
Number of circularly symmetric neighbour set points (quantization of the angular space).
R: float
Radius of circle (spatial resolution of the operator).
method: {‘default’, ‘ror’, ‘uniform’, ‘var’}
Method to determine the pattern.
- ‘default’: original local binary pattern which is gray scale but not rotation invariant.
- ‘ror’: extension of default implementation which is gray scale and rotation invariant.
- ‘uniform’: improved rotation invariance with uniform patterns and finer quantization of the angular space which is gray scale and rotation invariant.
- ‘nri_uniform’: non rotation-invariant uniform patterns variant which is only gray scale invariant.
- ‘var’: rotation invariant variance measures of the contrast of local image texture which is rotation but not gray scale invariant.
Returns
output: (N, M) array
LBP image.
四、基于python-opencv的LBP实现
LBP常应用于人脸识别和目标检测中,在OpenCV中有使用LBP特征进行人脸识别的接口,也有用LBP特征训练目标检测分类器的方法,OpenCV实现了LBP特征的计算,但没有提供一个单独的计算LBP特征的接口。也就是说OpenCV中使用了LBP算法,但是没有提供函数接口。
opencv提供了一个级联分类器,可以进行人脸检测,该分类器不仅可以使用Harr,也可以使用LBP特征。具体使用可以参考文章《浅析cv2.CascadeClassifier()函数》
将lbpcascade_frontalface_improved.xml下载至本地以方便调用,下载链接:https://github.com/opencv/opencv/blob/master/data/lbpcascades/lbpcascade_frontalface_improved.xml
#coding:utf-8
import cv2 as cv
# 读取原始图像
img= cv.imread('*.png')
#face_detect = cv2.CascadeClassifier('haarcascade_frontalface_default.xml')
face_detect = cv.CascadeClassifier("lbpcascade_frontalface_improved.xml")
# 检测人脸
# 灰度处理
gray = cv.cvtColor(img, code=cv.COLOR_BGR2GRAY)
# 检查人脸 按照1.1倍放到 周围最小像素为5
face_zone = face_detect.detectMultiScale(gray, scaleFactor = 2, minNeighbors = 2) # maxSize = (55,55)
print ('识别人脸的信息:\n',face_zone)
# 绘制矩形和圆形检测人脸
for x, y, w, h in face_zone:
# 绘制矩形人脸区域
cv.rectangle(img, pt1 = (x, y), pt2 = (x+w, y+h), color = [0,0,255], thickness=2)
# 绘制圆形人脸区域 radius表示半径
#cv.circle(img, center = (x + w//2, y + h//2), radius = w//2, color = [0,255,0], thickness = 2)
# 设置图片可以手动调节大小
cv.namedWindow("Easmount-CSDN", 0)
# 显示图片
cv.imshow("Easmount-CSDN", img)
# 等待显示 设置任意键退出程序
cv.waitKey(0)
cv.destroyAllWindows()
参考
LBP纹理特征提取学习笔记
local_binary_pattern参考文档
Datawhale计算机视觉基础-图像处理(下)-Task02 LBP特征描述算子-人脸检测
