UESTC 1690 这是一道比CCCC简单题难的简单题||HiHoCoder #1048 : 状态压缩·二
这道题搞了很久终于搞懂了,感觉受益匪浅,先贴上题目:
题目一:UESTC 1690 这是一道比CCCC简单题难的简单题
这是一道比CCCC简单题难的简单题
Time Limit: 3000/1000MS (Java/Others) Memory Limit:65535/262140KB (Java/Others)
集训队的CFT大爷精通Python
有一天,CFT大爷跑在vps上的python爬虫程序挂了
CFT大爷经过缜密的推断,发现程序挂了的原因是Python的垃圾回收机制不够优越,导致内存炸了,那些卖vps的奸商强行杀掉了他的爬虫程序
CFT大爷决定再也不用python这门垃圾语言,他要发明一个新的语言CFTthon
CFT大爷的CFTthon是跑在CFT大爷以前写的CFT_OS上的,在CFT_OS中,内存布局是一个n*m的长方形矩阵,而CFTthon所有的变量,都只占用1*2大小的小长方形内存空间。
CFT大爷在手写CFTthon的GC系统时,想到了一个问题:给定n,m,要求用CFTthon的变量把整个内存空间完全覆盖,不重合不遗漏,有多少种方法呢?
**** 扯淡题意分割线 ****
给定一个n*m的矩阵,使用1*2的小长方形覆盖矩阵,要求完全覆盖的同时不出现重合,也不允许超出边界,问有多少种可能的覆盖方法,方案数对1e9+7取模
2<=n<=1000
3<=m<=5
Input
整数n,m
Output
方案数
Sample input and output
| Sample Input |
Sample Output |
2 4 |
5 |
题目二:HiHoCoder #1048 : 状态压缩·二
描述
历经千辛万苦,小Hi和小Ho终于到达了举办美食节的城市!虽然人山人海,但小Hi和小Ho仍然抑制不住兴奋之情,他们放下行李便投入到了美食节的活动当中。美食节的各个摊位上各自有着非常多的有意思的小游戏,其中一个便是这样子的:
小Hi和小Ho领到了一个大小为N*M的长方形盘子,他们可以用这个盒子来装一些大小为2*1的蛋糕。但是根据要求,他们一定要将这个盘子装的满满的,一点缝隙也不能留下来,才能够将这些蛋糕带走。
这么简单的问题自然难不倒小Hi和小Ho,于是他们很快的就拿着蛋糕离开了~
但小Ho却不只满足于此,于是他提出了一个问题——他们有多少种方案来装满这个N*M的盘子呢?
值得注意的是,这个长方形盘子的上下左右是有区别的,如在N=4, M=3的时候,下面的两种方案被视为不同的两种方案哦!
提示:我们来玩拼图吧!不过不同的枚举方式会导致不同的结果哦!
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第一行为两个正整数N、M,表示小Hi和小Ho拿到的盘子的大小。
对于100%的数据,满足2<=N<=1000, 3<=m<=5。
输出
考虑到总的方案数可能非常大,只需要输出方案数除以1000000007的余数。
2 4
样例输出
5
分析:
其实这两道题本质是完全一样的,就是用1*2的小长方形完全覆盖n * m的矩形有多少方案。
下面分析如何用状态压缩DP来解这道题(如果不理解为什么要用DP,为什么要用状压DP见hihoCoder题目中的提示链接,虽然我也看得云里雾里)
DP顾名思义,我们需要用到状态转移,假设我们现在正在考虑(i,j)这个位置该怎么放(此时这个位置之前的位置已经铺好了)。有三种情况:
- 不需要铺砖,因为在位置(i-1,j)铺的是竖砖,(i,j)已经被铺好了。(为什么不用考虑(i,j-1)铺横砖在下面会解释)
- 铺横砖,那么(i,j+1)也就被同时铺好了,直接考虑(i,j+2),这正解释了(1)中为什么不用考虑(i,j-1)铺横砖的情况。
- 铺竖砖,那么(i+1,j)也就被同时铺好了.
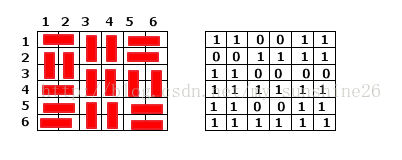
鉴于以上几种情况,我们将每一个位置的状态用0或1来表示,如果我们在(i,j)铺横砖,那么(i,j)和(i,j+1)都为1,如果我们在(i,j)铺竖砖,那么(i,j)为0,(i,j+1)为1。
可以用下面的图片增进理解:
那为什么要这样定义呢,我们可以这么认为,某一个位置的状态为1则表示它对下一行的状态没有限制,而为0时,表示它对下一行的状态有限制(必须为1)。(读者可以将上面的两种情况自己模拟一下)
然后下一步我们要做的就是对每个位置的放置方法进行检测可行性,并对它计数。
我们先用一个数来表示某一行的状态,这个数转化为二进制数后,第i个数*(0/1)代表该行第i列的状态。我们需要做的便是判断相邻行的状态是否合法。
判断方法的解析见代码中的注释。
由于第一行没有前驱,我们先对第一行进行特判,然后再从第二行开始进行状态转移。
用dp[i][j]表示铺到第i行,且第i行的状态为j时的总方案数。容易写出状态转移方程为dp[i][j]=dp[i][j]+dp[i-1][k](dp[i][j]一定等于i-1行能与j状态兼容的所有方案数和)
由于最后一行的状态不可能出现0,所以结果就是dp[n-1][total-1],
(计算过程中注意取模)
#include
#include
#include
#include
#include
#include
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define f(i,a,b) for(int i=(a);i<=(b);++i)
#define rush() int T;scanf("%d",&T);while(T--)
typedef long long ll;
const int maxn= 1005;
const ll mod = 1e9+7;
const int INF = 0x3f3f3f3f;
const double eps = 1e-6;
ll dp[maxn][1<<5];
bool one(int state,int len) //检测某一行内部的状态是否满足要求
{
int pos=0;
while(posn) //优化,因为此题时间、空间主要消耗在每一行的多种状态上
swap(m,n);
int total=1<