Controllable Person Image Synthesis with Attribute-Decomposed GAN（CVPR20）

3. Method Description

framework中涉及到pose $P\in {\mathbb{R}}^{18\times H\times W}$表示为18通道的heatmap

3.1. Generator

Generator的输入为source person image $I_s$和target pose $P_t$，输出为generated image $I_g$

一个常见的做法是将$I_s$和$P_t$拼接起来送入生成器
本文将$I_s$和$P_t$编码为latent code，分别叫做pose encoding和decomposed component encoding

3.1.1 Pose encoding

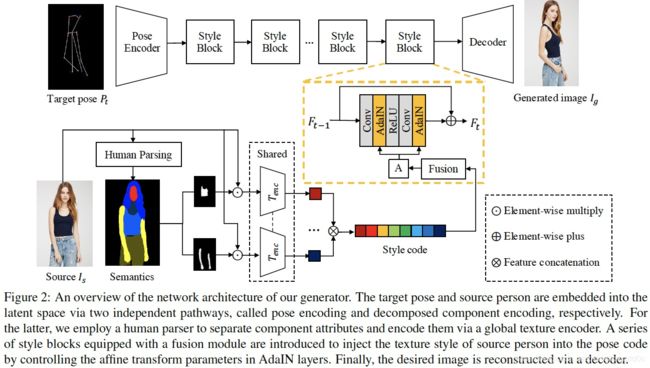
如Fig.2上方所示，target pose $P_t$输入pose encoder（是一个2层down-sampling convolutional layers结构），得到pose code $C_{pose}$

3.1.2 Decomposed component encoding（DCE）

对source person image $I_s$提取semantic map $S$，将$S$表示为$K$通道的heatmap $M\in {\mathbb{R}}^{K\times H\times W}$，$K$为human parser的分割类别（实验中$K=8$，包括background, hair, face, upper clothes, pants, skirt, arm and leg），每一个通道是一个binary mask $M_i\in {\mathbb{R}}^{H\times W}$，与$I_s$进行点乘，就得到了decomposed person image，即通过分割mask完成了source image每一个component的分解
$$I_s^i=I_s\odot M_i(1)$$
然后将每一个$I_s^i$送入texture encoder $T_{enc}$，得到style code $C_{sty}^i$
$$C_{sty}^i=T_{enc}\left(I_s^i\right)(2)$$
将style code $C_{sty}^i$拼接到一起，得到full style code $C_{sty}$，见Fig.2中的$\otimes$操作

In contrast to the common solution that directly encodes the entire source person image, this intuitive DCE module decomposes the source person into multiple components and recombines their latent codes to construct the full style code.

仔细想想，DCE的做法其实是等价于local patch的做法的，都是分离出不同的部分，单独进行处理

作者认为DCE有2点好处

1. 能加速模型收敛
2. 这是一种无监督的attribute separation方式，semantic map是human parser白送的，不需要任何annotation
   
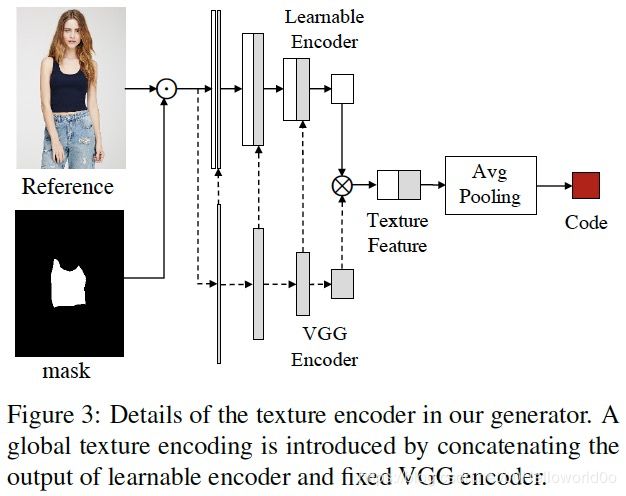
   下面介绍texture encoder的结构，如Fig.3所示，texture encoder其实包含了2个encoder，Learnable Encoder和VGG Encoder（pretrained on the COCO dataset），这种双Encoder的方式称为global texture encoding（GTE）

Fig.4展示了DCE和GTE的效果

3.1.3 Texture style transfer

Texture style transfer的目标是将source image的texture迁移到target pose上，是联系style code和pose code的桥梁

transfer network级联了若干个style block，内部细节见Fig.2黄色框

对于第$t$个style block，输入是前一个feature map $F_{t-1}$和full style code $C_{sty}$，通过残差的方式得到输出的feature map $F_t$
$$F_t={\varphi }_t\left(F_{t-1},A\right)+F_{t-1}(3)$$

令$F_0=C_{pose}$，总共设置8个style block

Fig.2中的$A$表示affine transform，输出scale $\mu$和shift $\sigma$用于执行AdaIN
Fig.2中的方框Fusion表示fusion module，包含3个fully connected layer，前两个layer用于select the desired features via linear recombination，最后一个layer用于维度变换

3.1.4 Person image reconstruction

将最后一个style block的输出送入decoder，得到生成结果$I_g$

3.2. Discriminators

参考文献[46]，设置2个判别器$D_p$和$D_t$，$D_p$用于使$I_g$具备target pose $P_t$，$D_t$用于使$I_g$的texture与$I_s$相似

对于$D_p$，假样本定义为$\left(P_t,I_g\right)$，真样本定义为$\left(P_t,I_t\right)$
注：数据集的特点是同一个人穿某件衣服，摆出不同pose，所以$I_t$其实是ground-truth

3.3. Training

$${\mathcal{L}}_{total}={\mathcal{L}}_{adv}+{\lambda }_{rec}{\mathcal{L}}_{rec}+{\lambda }_{per}{\mathcal{L}}_{per}+{\lambda }_{CV}{\mathcal{L}}_{CX}(4)$$

Adversarial loss

这里梳理一下${\mathcal{L}}_{adv}$所涉及的变量：原图$I_s$指定$P_t$生成$I_g=G(I_s,P_t)$，ground-truth为$I_t$
$$\begin{array}{rl}{\mathcal{L}}_{adv}=& {\mathbb{E}}_{I_s,P_t,I_t}\left[\log \left(D_t(I_s,I_t)\cdot D_p(P_t,I_t)\right)\right]+\\ & {\mathbb{E}}_{I_s,P_t}\left[\log \left(1-D(I_s,I_g)\right)\cdot \log \left(1-D(P_t,I_g)\right)\right](5)\end{array}$$
注：这个公式使用了一个符号$\cdot$，还是能够明白公式所表达的意思

Reconstruction loss

因为有ground-truth $I_t$，所以直接最小化$I_g$与$I_t$之间的误差
$${\mathcal{L}}_{rec}={\Vert I_g-I_t\Vert }_1(6)$$
注：因为有了ground-truth，所以就不需要一个令$I_g$有$P_t$的pose loss了

Perceptual loss

利用pretrained VGG19，取layer $l=relu\left\{3\_2,4\_2\right\}$，${\mathcal{F}}^l$就对应了VGG19 layer $l$的feature map

作者认为visual style statistics本质上是feature correlations，所以考虑$I_g$和$I_t$的Gram matrix，以$I_t$为例，Gram matrix计算如下
$$\mathcal{G}\left({\mathcal{F}}^l(I_t)\right)=\left[{\mathcal{F}}^l(I_t)\right]{\left[{\mathcal{F}}^l(I_t)\right]}^T(7)$$
于是perceptual loss令$I_g$和$I_t$的Gram matrix之间的差异最小化
$${\mathcal{L}}_{per}={\Vert \mathcal{G}\left({\mathcal{F}}^l(I_g)\right)-\mathcal{G}\left({\mathcal{F}}^l(I_t)\right)\Vert }^2(8)$$

Contextual loss

Contextual loss是文献[25]提出的
$${\mathcal{L}}_{CX}=-\log \left(CX\left({\mathcal{F}}^l(I_g),{\mathcal{F}}^l(I_t)\right)\right)(9)$$
其中$CX$表示2个feature map之间的相似性度量，若similarity越大，则$-\log \left(\text{similarity}\right)$的值就越小
Q：不是很明白为什么要加一个$\log$

Implementation details

实验中设置${\lambda }_{rec}=2,{\lambda }_{per}=2,{\lambda }_{CX}=0.02$
总共训练120k iterations，学习率设置为0.001，从60k iteration开始，线性衰减到0
注：文中没说batch size是多少