笔记-编译原理-第十、十一、十二章、十三章-语法分析-自下而上分析

第10章 - 自下而上分析1

10.1 自下而上分析

10.1.1 自下而上分析的一个示例

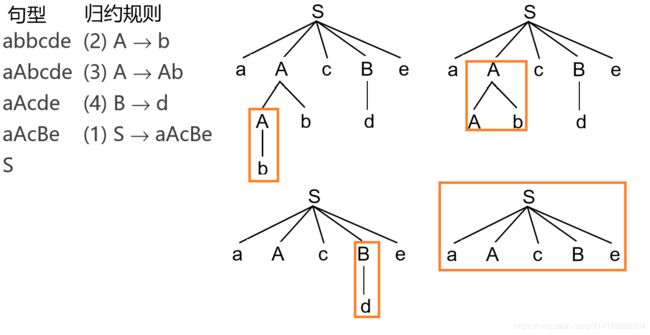
可以看出自下而上分析的主要步骤是不断的用文法来“规约”，最后找到一种句型的表示

10.1.2 自下而上分析的基本思想

• 采用 “移进－归约” 思想进行自下而上分析
• 基本思想: 用一个寄存符号的先进后出栈，把输入符号一个一 个地移进到栈里，当栈顶形成某个产生式的候选式 时，即把栈顶的这一部分替换成(归约为)该产生式的 左部符号。

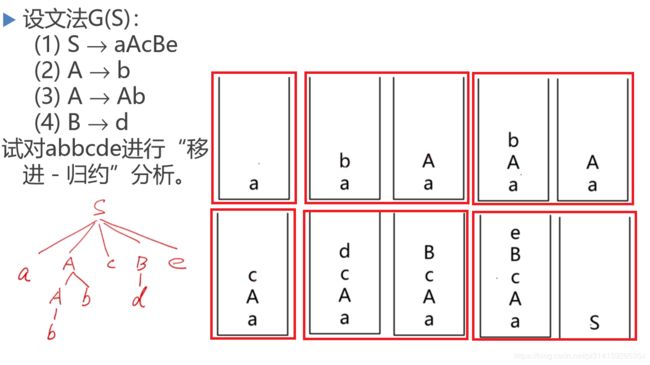
10.1.3 移进－归约分析示例

其中每一步的操作都可以构成语法树（分析树）的一部分。

什么是可归约串：短语

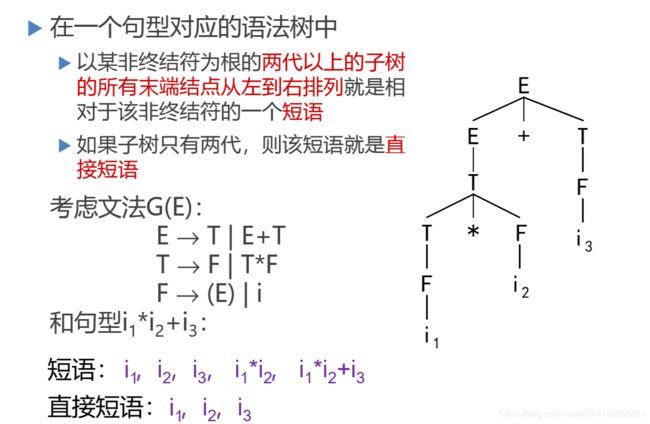
10.2 短语与直接短语

10.2.1 短语

• 定义：令G是一个文法，S是文法的开始符号， 假定 $\alpha \beta \delta$ 是文法G的一个句型，如果有 $S{\Rightarrow }^{\ast }\alpha A\delta 且A{\Rightarrow }^{+}\beta$ 则 β称是句型 $\alpha \beta \delta$ 相对于非终结符A的短
• 如果有 $A\Rightarrow \beta$ ,则称 $\beta$ 是句型 $\alpha \beta \delta$ 相对于规则 $A\to \beta$ 的 直接短语。

10.2.2 测试：短语和直接短语

10.3 分析过程描述

10.4 算符优先文法

10.4.1 算符优先文法

算符优先分析法:

• 按照算符的优先关系和结合性质进行语法分析
• 适合分析表达式

LR分析法:

• 规范归约：句柄作为可归约串

10.4.2 运算的优先级

四则运算的优先规则: 先乘除后加减，同级从左到右

考虑文法G’(E)： E →i| E+E | E-E | E*E | E/E | (E) : 句子i+i-i*(i+i)有几种不同的归约 :

归约顺序不同，计算的顺序也不 同，结果也不一样；归约顺序不同，计算的顺序也不 同，结果也不一样。

句子i+i-i*(i+i)的归约过程：

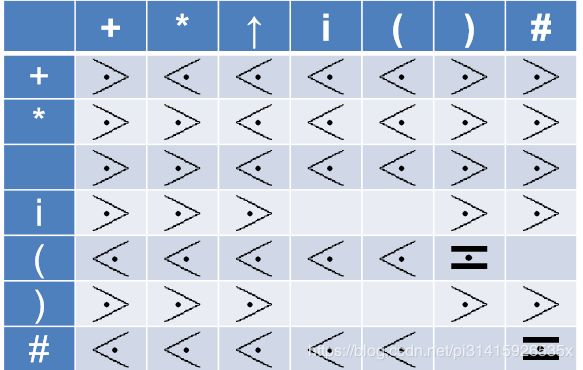
10.4.3 优先关系

任何两个可能相继出现的终结符a与b可能三种 优先关系 ：

• $a⋖b$ a的优先级低于b
• $a\doteq b$ a的优先级等于b （这里的点是在等号中间的，找不到对应的latex了，就用在上面的表示了，有知道的告诉我一下，谢谢啦）
• $a⋗b$ a的优先级高于b

算符优先关系与数学上的<>=不同 :

• $+⋖+$
• $a⋖b$ 并不意味着 $b⋗a$ 如 $(⋖+和+⋖($

10.4.4 算符文法

一个文法，如果它的任一产生式的右部都不含 两个相继(并列)的非终结符，即不含 $\dots QR\dots$ 形式的产生式右部，则我们称该文法为算符文法。

约定：

• a、b代表任意终结符
• P、Q、R代表任意非终结符
• ‘…’代表由终结符和非终结符组成的任意序列，包括空字

10.4.5 算符优先文法

示例：算符优先文法：

对应的优先关系表：

10.5 构造优先关系表

10.5.1 构造优先关系表的算法——FIRSTVT和LASTVT集合

根据FIRSTVT和LASTVT集合，检查每个产生式 的候选式，确定满足关系 $⋖$ 和 $⋗$ 的所有终结符对 ：

• 假定有个产生式的一个候选形为…aP…，那么，对 任何 $b\in FIRSTVT(P)$ ，有 $a⋖b$
• 假定有个产生式的一个候选形为…Pb…，那么，对 任何 $a\in LASTVT(P)$ ，有 $a⋗b$

10.5.2 构造集合FIRSTVT§的算法

反复使用下面两条规则构造集合 $FIRSTVT(P)$ :

• 若有产生式 $P\to a\dots$ 或 $P\to Qa\dots$ ，则 $a\in FIRSTVT(P)$
• 若 $a\in FIRSTVT(Q)$ ，且有产生式 $P\to Q\dots$ ，则 $a\in FIRSTVT(P)$

算法的一种实现:

• 布尔数组F[P，a] ，使得F[P，a]为真的条件是，当且 仅当a∈FIRSTVT§。开始时，按上述的规则1对每 个数组元素F[P，a]赋初值。
• 栈STACK ，把所有初值为真的数组元素F[P，a]的符 号对(P，a)全都放在STACK之中。
• 若栈STACK不空，就将栈顶项弹出，记此项为 (Q， a) 。对于每个形如 P→Q… 的产生式，若F[P，a]为假， 则变其值为真且将 (P，a) 推进STACK栈。
• 上述过程一直重复，直至栈STACK为空为止。

算法的工作结果得到一个二维数组F，从它可得 任何非终结符P的FIRSTVT $FIRSTVT(P)＝\{a|F[P，a]=TRUE\}$

10.5.3 构造集合LASTVT§的算法

同样的思想：

反复使用下面两条规则构造集合LASTVT§

• 若有产生式 $P\to \dots a$ 或 $P\to \dots aQ$ ，则 $a\in LASTVT(P)$
• 若 $a\in LASTVT(Q)$ ，且有产生式 $P\to \dots Q$，则 $a\in LASTVT(P)$

10.5.4 FIRSTVT和LASTVT集合计算示例

10.5.5 构造优先关系表的算法

• 通过检查G的每个产生式的每个候选式，可找 出所有满足 $a\doteq b$ 的终结符对。
• 根据FIRSTVT和LASTVT集合，检查每个产生式 的候选式，确定满足关系 $⋖$ 和 $⋗$ 的所有终结符对
  • 假定有个产生式的一个候选形为 $\dots aP\dots$ ，那么，对 任何 $b\in FIRSTVT(P)$ ，有 $a⋖b$
  • 假定有个产生式的一个候选形为 $\dots Pb\dots$ ，那么，对 任何 $a\in LASTVT(P)$ ，有 $a⋗b$

10.5.6 示例：构造优先关系表

对于#的判断可以通过句型： #E# 来判断。

没有任何两个终结符之间是有多个关系的，所以该文法是一个算符优先文法。

10.6 算符优先分析算法

10.6.1 最左素短语

• 可归约串，句型，短语
• 一个文法G的句型的 素短语 是指这样一个短语， 它至少含有一个终结符，并且，除它自身之外 不再含任何更小的素短语
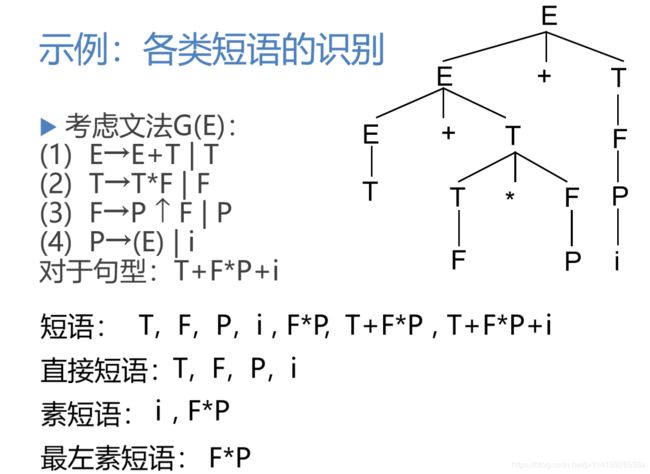
• 最左素短语 是指处于句型左边的那个素短语
  

10.6.2 最左素短语定理

• 算符优先文法句型(括在两个＃之间)的一般形式： $\#N_1{a}_1{N}_2{a}_2\dots N_n{a}_n{N}_{n+1}\#$ 其中， $a_i$ 都是终结符，$N_i$ 是可有可无的非终结符。
• 定理：一个算符优先文法G的任何句型的左素短语是 满足如下条件的左子串 $N_j{a}_j\dots N_i{a}_i{N}_{i+1}$ ， 且：
  • $a_{j-1}⋖a_j$
  • $a_j\doteq a_{j+1},\dots ,a_{i-1}\doteq a_i$
  • $a_i⋗a_{i+1}$
    

10.6.3 算符优先分析算法

• 使用一个符号栈S，用它寄存终结符和非终结符， k代表符号栈S的使用深度
• 在正确的情况下，算法工作完毕时，符号栈S应 呈现：# N #

整个算法的执行如下：

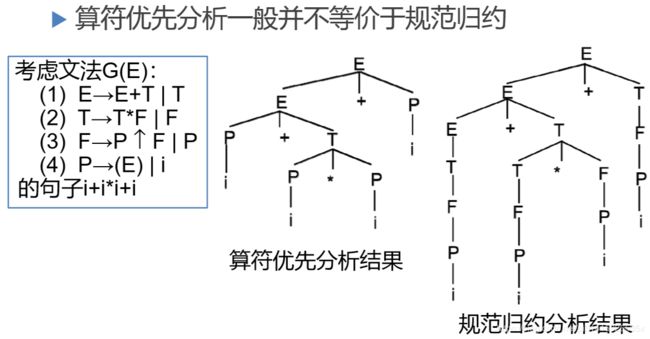
根据上面的规约那一部分的算法可知：对于文法的句子来说，它的算符优先分析的结果 不一定 就是语法树，所以语法树和分析树要分开指代，这章一开始便已强调：

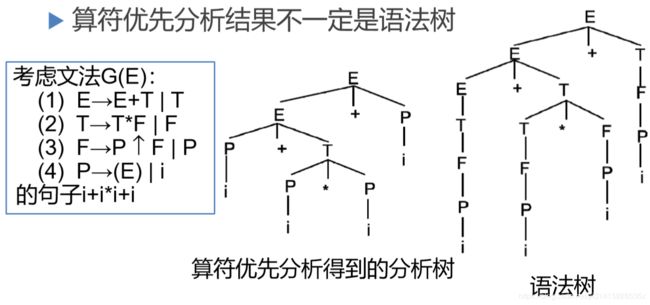
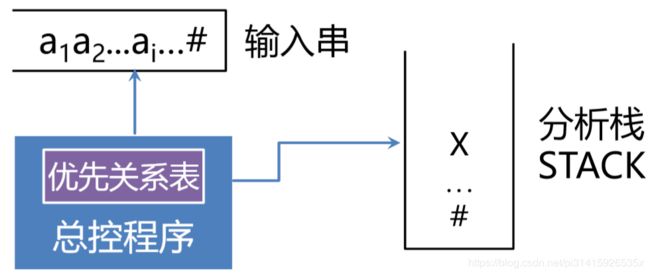
10.6.4 算符优先分析程序构成

• 总控程序 ，根据现行栈顶符号和当前输入符号， 执行动作
• 优先关系表 ，用于指导总控程序进行移进-归约
• 分析栈STACK ，用于存放文法符号
  

10.6.5 算符优先分析法

特点:

• 优点: 简单，快速
• 缺点: 可能错误接受非法句子

使用广泛,用于分析各类表达式 如，ALGOL 60

第11章 自下而上分析2

11.1 LR分析法概述

11.1.1 LR分析法

• 1965年由Knuth提出
• L：从左到右扫描输入串
• R：自下而上进行归约

11.1.2 工作框架

11.2 句柄和规范归约

11.2.1 短语、直接短语和句柄

• 短语 :定义：令G是一个文法，S是文法的开始符号， 假定αβδ是文法G的一个句型，如果有 $S{\Rightarrow }^{\ast }\alpha A\delta 且A{\Rightarrow }^{+}\beta$ ，则称 $\beta$ 是句型 $\alpha \beta \delta$ 相对于非终结符A的短语。
• 直接短语 : 如果有 $A\Rightarrow \beta$ ,则称β是句型 $\alpha \beta \delta$ 相对于规则 $A\to \beta$ 的直接短语。
• 句柄 :一个句型的左直接短语称为该句型的句柄。

11.2.2 用句柄归约

可用句柄来对句子进行归约:

11.2.3 规范归约

定义：假定 $\alpha$ 是文法G的一个句子，我们称序列 ${\alpha }_n，{\alpha }_{n-1}，\dots ，$ ${\alpha }_0$ 是 $\alpha$ 的一个规范归约，如果此序列满足：

• ${\alpha }_n=\alpha$
• ${\alpha }_0$ 为文法的开始符号，即 ${\alpha }_0=S$
• 对任何i，$0\le i\le n$ ，${\alpha }_{i-1}$是从 ${\alpha }_i$ 经把句柄替换成为相应产生式左部符号而得到的

11.2.4 算符优先分析vs. 规范归约

11.2.5 规范句型

• 规范归约 是最左归约
• 规范归约的逆过程就是右推导 $S\Rightarrow aAcBe\Rightarrow aAcde\Rightarrow aAbcde\Rightarrow abbcde$
• 右推导也称为 规范推导
• 由规范推导推出的句型称为 规范句型

11.3 LR分析法

11.3.1 规约的关键

规范归约的关键问题是寻找句柄.

• 历史 ：已移入符号栈的内容
• 展望 ：根据产生式推测未来可能遇到的输入符号
• 现实 ：当前的输入符号

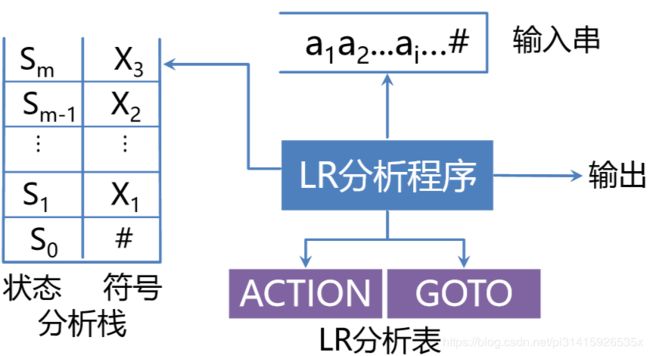
11.3.2 LR分析器的结构

LR分析方法：把 "历史" 及 "展望" 综合抽象成状态 ；由栈顶的 状态 和 现行的输入符号 唯一确定每一步工作:

11.3.3 LR分析表

LR分析器的核心是一张分析表:

• ACTION[s，a] ：当状态s面临输入符号a时，应采取什么动作.
• GOTO[s，X] ：状态s面对文法符号X时，下一状态是什么

11.3.4 LR分析过程

• 分析开始时：

状态栈	符号栈	输入串
$(s_0,$	$\#,$	$a_1{a}_2\dots a_n\#)$

• 以后每步的结果可以表示为:

状态栈	符号栈	输入串
$(s_0{s}_1\dots s_m,$	$\#X_1\dots X_m,$	$a_i{a}_{i+1}\dots a_n\#)$

11.3.5 LR分析示例

11.3.6 LR分析器的性质

• 栈内的符号串和扫描剩下的输入符号串构成了一个规范句型
• 一旦栈的顶部出现可归约串(句柄)，则进行规约

对于句子，在规范归约过程中，栈内的符号串 和扫描剩下的输入符号串构成了一个规范句型， 下面哪种格局不会出现：

11.4 LR文法

11.4.1 LR文法

• 定义：对于一个文法，如果能够构造一张分析表，使得它的每个入口均是唯一确定的，则这 个文法就称为 LR文法 。
• 定义：一个文法，如果能用一个每步顶多向前检查k个输入符号的LR分析器进行分析，则这 个文法就称为 LR(k)文法 。

11.4.2 LR文法与二义文法

• LR文法不是二义的，二义文法肯定不会是LR的
• LR文法⊂无二义文法
• 非LR结构:

第12章 自下而上分析3

12.1 活前缀

12.1.1 字的前缀、活前缀

• 字的前缀 ：是指字的任意首部，如字 abc 的前缀 有ε， a ， ab ， abc
• 活前缀 ：是指 规范句型 的一个前缀，这种前缀不含 句柄 之后的任何符号。即，对于规范句型 $\alpha \beta \delta$ ，$\beta$ 为句柄，如果 $\alpha \beta =u_1{u}_2\dots u_r$，则符号串 $u_1{u}_2\dots u_i(1\le i\le r)$ 是 $\alpha \beta \delta$ 的 活前缀 。( $\delta$ 必为终结符串)
• 规范归约过程中，保证分析栈中总是 活前缀 ， 就说明分析采取的移进/归约动作是正确的

对于一个文法G, 可以构造一个DFA,它能识别G 的所有活前缀。

12.2 构造识别活前缀的DFA

12.2.1 文法的拓广

将文法 $G(S)$ 拓广为 $G^{\prime }(S)$ :

• 构造文法 $G^{\prime }$ ，它包含了整个 $G$ ，并引进不出现在 $G$ 中的非终结符 $S^{\prime }$ 、以及产生式 $S^{\prime }\to S$ ，$S^{\prime }$ 是 $G^{\prime }$ 的开始符号
• 称 $G^{\prime }$ 是 $G$ 的拓广文法

12.2.2 LR(0)项目

• LR(0)项目: 在每个产生式的右部添加一个圆点，表示我们在分析过程中看到了产生式多大部分
• 例如： $A\to XYZ$ 有四个项目：$A\to •XYZA\to X•YZA\to XY•ZA\to XYZ•$
• $A\to \alpha •$ 称为 "归约项目" （把点看成识别的指针，识别到产生的末表示可以用这个产生式的左部代替）
• 归约项目 $S^{\prime }\to \alpha •$ 称为 "接受项目"（表示识别到文法的拓广文法的开始，也就是当前读入的单词被识别到了）
• $A\to \alpha •a\beta (a\in VT)$ 称为 "移进项目"
• $A\to \alpha •B\beta (B\in VN)$ 称为 "待约项目"

示例：

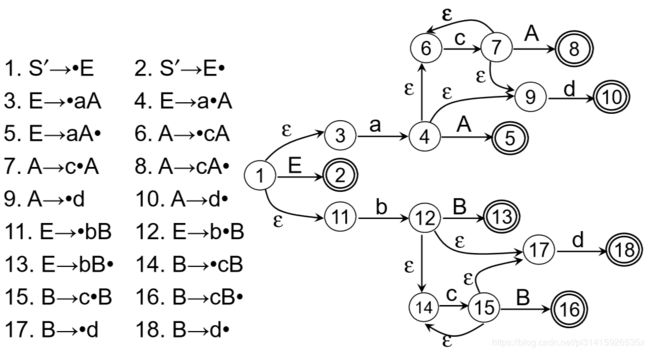
12.2.3 构造识别文法所有活前缀的DFA

对于上面那个文法的一个NFA就是：

然后按照前面的套路将NFA变为DFA：

12.2.4 LR(0)项目集规范族

构成识别一个文法活前缀的DFA的项目集(状 态)的全体称为文法的 LR(0)项目集规范族 。

如上图中的每一个状态中的一些项目组成的集合就是一个个 项目集规范族：

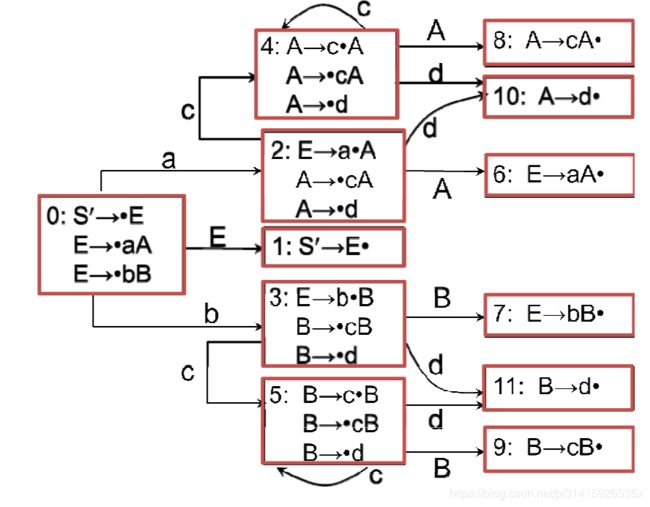
12.3 通过计算项目集规范族构造识别活前缀的DFA

12.3.1 有效项目

项目 $A\to {\beta }_1•{\beta }_2$ 对活前缀 $\alpha {\beta }_1$ 是有效的，其条件是存在规范推导： $$S^{\prime }{\Rightarrow }_R^{\ast }\alpha A\omega {\Rightarrow }_R^{\ast }\alpha {\beta }_1{\beta }_2\omega$$

在任何时候，分析栈中的活前缀 $X_1{X}_2\dots X_m$ 的有效项目集正是从 识别活前缀的DFA的 初态出发，读出 $X_1{X}_2\dots X_m$ 后到达的那个项目集(状态)。

（应该可以理解为当一个活前缀的后缀是某个项目的前缀时，就称这个项目是这个活前缀的一个有效项目，因为只要当活前缀的后缀加上一定的后续的读入就可以规约到这个项目的左部）

12.3.2 有效项目的性质

若项目 $A\to \alpha •B\beta$ 对活前缀 $\eta =\delta \alpha$ 是有效的且 $B\to \gamma$ 是一个产生式，则项目 $B\to •\gamma$ 对 $\eta =\delta \alpha$ 也是有效的。

证明：

12.3.3 LR(0)项目集规范族的构造

将文法G(S)拓广为G′(S′)：

• 构造文法G′，它包含了整个G，并引进不出现在G中 的非终结符S′、以及产生式S′→S，S′是G′的开始符 号
• G′唯一的“接受”态：仅含项目S′→S•的状态

12.3.4 项目集的闭包CLOSURE

12.3.5 状态转换函数

为了识别活前缀，我们定义一个状态转换函数GO。I是一个项目集，X是 一个文法符号。函数值GO(I，X)定义为： $GO(I，X)＝CLOSURE(J)$ 其中 $J＝\{任何形如A\to \alpha X•\beta 的项目|A\to \alpha •X\beta 属于I\}$。

直观上说，若 $I$ 是对某个活前缀 $\gamma$ 有效的项目集， 那么，$GO(I，X)$ 便是对 $\gamma X$ 有效的项目集

12.3.6 示例：项目集的转移函数计算

12.3.7 LR(0)项目集规范族的构造算法

PROCEDURE ITEMSETS(G′)； 
BEGIN 
	C:={CLOSURE({S′→•S})}；
	REPEAT 
		 FOR C中每个项目集I和G′的每个符号X DO 
		 	IF GO(I，X)非空且不属于C THEN 
		 		把GO(I，X)放入C族中; 
	UNTIL C不再增大
END

12.3.8 两种构造识别活前缀的DFA的方法

• 1.项目→ NFA → DFA
• 2.Closure → GO → DFA

12.4 构造LR(0)分析表

12.4.1 LR(0)分析表的构造

假若一个文法G的拓广文法G′的活前缀识别自 动机中的每个状态(项目集)不存在下述情况：

• 既含移进项目又含归约项目；
• 含有多个归约项目

则称G是一个LR(0)文法。

12.4.2 构造LR(0)分析表的算法

• 令每个项目集 $I_k$ 的下标 $k$ 作为分析器的状态，包含项目 $S^{\prime }\to •S$ 的集合 $I_k$ 的下标 $k$ 为分析器的初态。
• 构造 $LR(0)$ 分析表的 $ACTION$ 和 $GOTO$ 子表

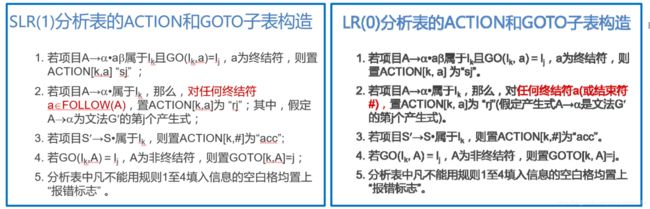
12.4.3 LR(0)分析表的ACTION和GOTO子表构造

• 1.若项目 $A\to \alpha •a\beta$ 属于 $I_k$且 $GO(I_k,a)＝I_j$ ，$a$为终结符，则置 $ACTION[k,a]$ 为“ $s_j$ ”。
• 2.若项目 $A\to \alpha •$ 属于 $I_k$ ，那么，对 任何终结符a(或结束符#) ， 置 $ACTION[k,a]$ 为“ $r_j$ ”(假定产生式 $A\to \alpha$ 是文法 $G^{\prime }$ 的第 $j$ 个产生式)。
• 3.若项目 $S^{\prime }\to S•$ 属于 $I_k$ ，则置 $ACTION[k,\#]$ 为“ $acc$ ”。
• 4.若 $GO(I_k,A)＝I_j$ ，$A$ 为非终结符，则置 $GOTO[k,A]=j$ 。
• 5.分析表中凡不能用规则1至4填入信息的空白格均置上 “报错标志”。

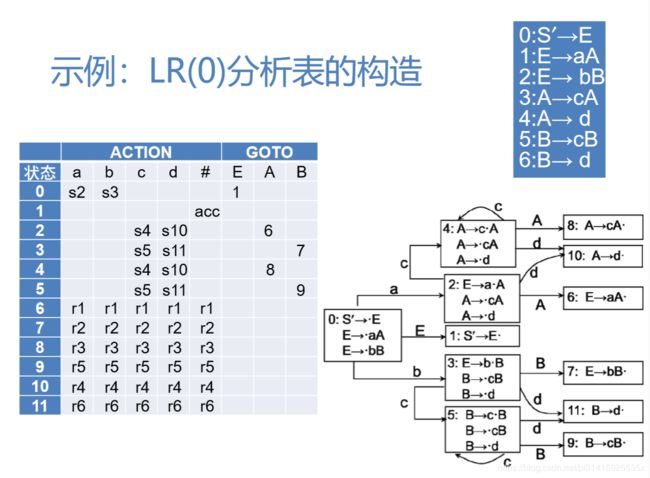
12.4.4 示例：LR(0)分析表的构造

12.4.5 LR(0)分析示例

第13章 自下而上分析4

13.1 SLR(1)分析法

13.1.1 一个非LR(0)文法

从这个文法的DFA可以看出，某些状态既是规约态，也是移进态，这样就是一个非LR(0)文法：

I1、I2和I9都含有“移进－归约”冲突，可以看出冲突的项目集中的项目的 FOLLOW集合是相交的。

13.1.2 冲突解决办法

• 假定一个LR(0)规范族含有如下的一个项目集 (状态) $I＝\{X\to \alpha •b\beta ，A\to \alpha •，B\to \alpha •\}$
• $FOLLOW(A)$ 和 $FOLLOW(B)$ 的交集为 $\varnothing$ ，且不包含 $b$
• 当状态 $I$ 面临任何输入符号 $a$ 时，可以:
  • $1.若a=b，则移进；$
  • $2.若a\in FOLLOW(A)，用产生式A\to \alpha 进行归约；$
  • $3.若a\in FOLLOW(B)，用产生式B\to \alpha 进行归约；$
  • 4.此外，报错。

13.1.3 SLR(1)冲突解决办法

假定LR(0)规范族的一个项目集 $I=\{A_1\to \alpha •a_1{\beta }_1，A2\to \alpha •a_2{\beta }_2，\dots ，A_m\to \alpha •a_m{\beta }_m，B_1\to \alpha •，B_2\to \alpha •，\dots ，B_n\to \alpha •\}$ 如果集合 $\{a_1，\dots ，a_m\}$，$FOLLOW(B_1)，\dots ，FOLLOW(B_n)$两两不相交(包括不得有两个FOLLOW集 合有#)，则当状态I面临任何输入符号a时：

• $1.若a是某个ai，i=1,2,\dots ,m，则移进；$
• $2.若a\in FOLLOW(B_i)，i=1,2,\dots ,n，则用产生式Bi\to \alpha 进行归约；$
• $3.此外，报错。$

SLR(1)解决办法：S-Simple，1-最多向前看一个单词

13.1.4 构造SLR(1)分析表的方法

• 把G拓广为G′
• 对G′构造
  • LR(0)项目集规范族C
  • 活前缀识别自动机的状态转换函数GO
• 使用C和GO，构造SLR分析表
  • 令每个项目集Ik的下标k作为分析器的状态，包含项 目S′→•S的集合Ik的下标k为分析器的初态。
  • 构造分析表的ACTION和GOTO子表

13.1.5 SLR(1)分析表的ACTION和GOTO子表构造

• 1.若项目 $A\to \alpha •a\beta$ 属于 $I_k$ 且 $GO(I_k,a)=I_j$ ，$a$ 为终结符，则置
  $ACTION[k,a]=s_j$；
• 2.若项目 $A\to \alpha •$ 属于 $I_k$ ，那么，对任何终结符 $a\in FOLLOW(A)$ ，置 $ACTION[k,a]$ 为“ $r_j$ ”；其中，假定 $A\to \alpha$ 为文法 $G^{\prime }$ 的第 $j$ 个产生式；
• 3.若项目 $S^{\prime }\to S•$ 属于 $I_k$ ，则置 $ACTION[k,\#]为“acc”$;
• 4.若 $GO(I_k,A)＝I_j$ ，$A$ 为非终结符，则置 $GOTO[k,A]=j$；
• 5.分析表中凡不能用规则1至4填入信息的空白格均置上 “报错标志” 。

13.1.6 SLR(1)和LR(0)分析表构造方法的对比

可以看出，SLR处理冲突的解决方法就是将以前分析表中规约的一行缩小成为FOLLOW的字符，减少冲突的可能（显然这样也不是最优的，也可能产生冲突的）

13.1.7 SLR(1)文法

• 按上述方法构造出的ACTION与GOTO表如果 不含多重入口，则称该文法为SLR(1)文法。
• 使用SLR表的分析器叫做一个SLR分析器。
• 每个SLR(1)文法都是无二义的。但也存在许多 无二义文法不是SLR(1)的。
• $LR(0)\subset SLR(1)\subset 无二义文法$

13.1.8 SLR(1)分析表构造示例

对于上面那个会产生冲突的LR(0)文法，更改其中产生 规约 步骤的分析表产生规则，使用FOLLOW来代替：

13.1.9 一个非SLR(1)文法

对于这样一个文法，它的SLR分析表是会产生冲突的：

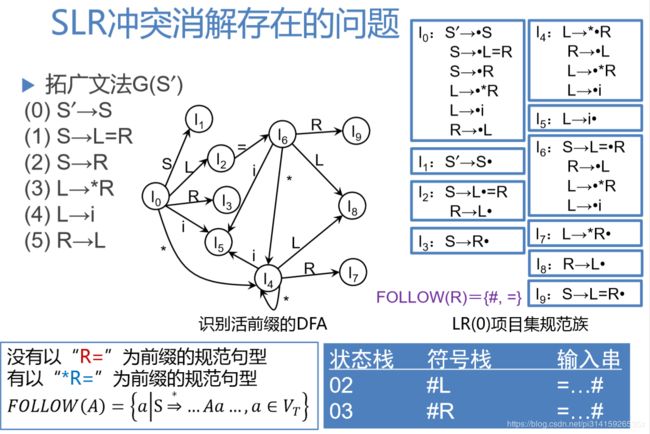
13.1.10 SLR冲突消解存在的问题

• SLR在方法中，如果项目集 $I_i$ 含项目 $A\to \alpha •$ 而且下一输入符号 $a\in FOLLOW(A)$ ，则状态 $i$ 面临 $a$ 时，可选用“用 $A\to \alpha$ 归约”动作
• 但在有些情况下，当状态i显现于栈顶时，当前单词是a， 栈里的 活前缀 $\beta \alpha$ 未必允许把 $\alpha$ 归约为 $A$ ，因为可能根本 就不存在一个形如“ $\beta Aa$ ”的规范句型
• 在这种情况下，用“A→α”归约不一定合适
• 原因是： FOLLOW集合提供的信息太泛 $FOLLOW(A)=\{\alpha |S{\Rightarrow }^{\ast }\dots A\alpha \dots ,\alpha \in V_T\}$

13.2 LR(1)分析表的构造

13.2.1 构造LR(1)分析表的方法

• 把G拓广为G′
• 对G′构造LR(1)项目集规范族C和活前缀识别自 动机的状态转换函数GO
• 使用C和GO，构造LR(1)分析表

13.2.2 LR(k)项目

• LR(k)项目 ：扩展LR(0)项目，附带有k个终结符 $[A\to \alpha •\beta ,a_1{a}_2\dots a_k]$ $a_1{a}_2\dots a_k$ 称为 向前搜索符串(或展望串) 。
• 归约项目 $[A\to \alpha •，a_1{a}_2\dots a_k]$ 的意义：当它所属的状态呈现在栈顶且后续的k个输入符号为 $a_1{a}_2\dots a_k$ 时，才可以把栈顶上的α归约为A
• 对于任何 移进 或 待约项目 $[A\to \alpha •\beta ,a_1{a}_2\dots a_k],\beta \ne \epsilon$ ，搜索符串 $a_1{a}_2\dots a_k$ 没有直接作用

13.2.3 有效项目

形式上我们说一个LR(1)项目 $[A\to \alpha •\beta ,a]$ 对于活前缀 $\gamma$ 是 有效的 ，如果存在规范推导 : $$S^{\prime }{\Rightarrow }_R^{\ast }\delta A\omega {\Rightarrow }_R^{\ast }\delta \alpha \beta \omega$$
其中，1) $\gamma ＝\delta \alpha$ ；2) $a$ 是 $\omega$ 的第一个符号，或者 $a$ 为#而 $\omega$ 为ε。

13.2.4 有效项目的性质

13.2.5 LR(1)项目集规范族

• 闭包函数CLOSURE
• 转换函数GO

项目集的闭包CLOSURE

假定I是文法G′的任一项目集，定义和构造I的闭 包CLOSURE(I)如下：

• 1.I的任何项目都属于 $CLOSURE(I)$ 。
• 2.若项目 $[A\to \alpha •B\beta ,a]$ 属于 $CLOSURE(I)$ ， $B\to \xi$ 是一个产生式，那么，对于 $FIRST(\beta a)$ 中的每个 终结符b，如果 $[B\to •\xi ,b]$ 原来不在 $CLOSURE(I)$ 中，则把它加进去。
• 3.重复执行步骤2，直至 $CLOSURE(I)$ 不再增大为止。

项目集的转换函数GO

令I是一个项目集，X是一个文法符号，函数 GO(I，X)定义为： $$GO(I，X)＝CLOSURE(J)$$ ,其中 $$J＝\{任何形如[A\to \alpha X•\beta ,a]的项目|[A\to \alpha •X\beta ,a]\in I\}$$

LR(1)项目集规范族的构造算法

BEGIN 
	C:={ CLOSURE( { [S′→•S，#] }) }; 
	REPEAT 
		FOR C中每个项目集I和G′的每个符号X DO 
			IF GO(I，X)非空且不属于C，THEN       
				把GO(I，X)加入C中 
	UNTIL C不再增大 
END

13.2.6 LR(1)分析表的构造算法

• 把G拓广为G′
• 对G′构造LR(1)项目集规范族C和活前缀识别自 动机的状态转换函数GO
• 使用C和GO，构造LR(1)分析表
  • 令每个Ik的下标k为分析表的状态，令含有[S′→•S, #] 的Ik的k为分析器的初态
  • 构造LR(1)分析表的ACTION和GOTO子表

13.2.7 LR(1)分析表的ACTION和GOTO子表构造

• 1.若项目[A→α•aβ, b]属于Ik且GO(Ik, a)＝Ij，a为 终结符，则置ACTION[k, a]为“sj”。
• 2.若项目[A→α•，a]属于Ik，则置ACTION[k, a]为 “rj”；其中假定A→α为文法G′的第j个产生式。
• 3.若项目[S′→S•, #]属于Ik，则置ACTION[k, #]为 “acc”。
• 4.若GO(Ik，A)＝Ij，则置GOTO[k, A]=j。
• 5.分析表中凡不能用规则1至4填入信息的空白栏 均填上“出错标志”。

13.2.8 LR(1)和SLR(1)分析表构造方法的对比

可以看出，与SLR相比，在规约中更加缩小了可规约的情况，使得冲突减小

13.2.9 LR(1)分析表和LR(1)文法

• 按上述算法构造的分析表，若不存在多重定义 的入口(即，动作冲突)的情形，则称它是文法G 的一张规范的LR(1)分析表。
• 具有规范的LR(1)分析表的文法称为一个LR(1)文法。
• 使用LR(1)分析表的分析器叫做一个规范的LR分析器。
• LR(1)状态比SLR(1)多
• $LR(0)\subset SLR(1)\subset LR(1)\subset 无二义文法$

13.2.10 LR(1)分析表构造示例

13.3 分析器产生工具

13.3.1 分析器产生器——YACC

YACC——Yet AnotherCompiler Compiler

• LALR(1)分析
• GNU Bison：基本兼容Yacc，与flex一起使用
• The Lex & YaccPage http://dinosaur.compilertools.net/

https://blog.csdn.net/pi31415926535x/article/details/105299131