排序二叉树的实现(java)

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

public class SortedBinTree4 {
    static class Node{
        Object data;
        Node parent;
        Node left;
        Node right;
        public Node(Object data, Node parent, Node left, Node right){
            this.data = data;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }

        public boolean equals(Object obj){
            if(obj == this){
                return true;
            }
            if(obj.getClass() == Node.class){
                Node node = (Node)obj;
                return this.data.equals(node.data)
                        && this.right == node.right
                        && this.left == node.left
                        && this.right == node.right;
            }
            return false;
        }
    }
    private Node root;
    public SortedBinTree4(){
        root = null;
    }
    public SortedBinTree4(T ele){
        root = new Node(ele, null, null, null);
    }

    public void addNode(T ele){
        if(root == null){
            root = new Node(ele, null, null, null);
        }else{
            Node cur = root;
            Node parent = null;
            int cmp = 0;
            do{
                cmp = ele.compareTo(cur.data);
                if(cmp > 0){
                    cur = cur.right;
                }else{
                    cur = cur.left;
                }
            }while(cur != null);
            Node node = new Node(ele, parent, null, null);
            if(cmp>0){
                parent.right = node;
            }else{
                parent.left = node;
            }

        }
    }

    public Node getNode(T ele){
        Node cur= root;
        int cmp = 0;
        while (cur!=null){
            cmp = ele.compareTo(cur.data);
            if(cmp > 0){
                cur = cur.right;
            }else if(cmp < 0){
                cur = cur.left;
            }else{
                return cur;
            }
        }
        return null;
    }

    public void removeNode(T ele){
        Node target = getNode(ele);
        if(target == null){
            return;
        }else{
            if(target.left == null && target.right == null){
                if(target == root){
                    root = null;
                }else{
                    if(target == target.parent.left){
                        target.parent.left = null;
                    }else{
                        target.parent.right = null;
                    }
                    target.parent = null;
                }
            }
            else if(target.left == null && target.right != null){
                if(target == root){
                    root = target.right;
                    root.parent = null;
                    target.right = null;
                }else{
                    if(target == target.parent.left){
                        target.parent.left = target.right;
                    }else{
                        target.parent.right = target.right;
                    }
                    target.right.parent = target.parent;
                    target.parent = target.right = null;
                }
            }
            else if(target.left != null && target.right == null){
                if(target == root){
                    root = target.left;
                    root.parent = null;
                    target.left = null;
                }else{
                    if(target == target.parent.left){
                        target.parent.left = target.left;
                    }else{
                        target.parent.right = target.left;
                    }
                    target.left.parent = target.parent;
                    target.parent = target.left = null;
                }
            }
            else {
               Node leftMaxNode = root.left;
               while (leftMaxNode.right!=null){
                   leftMaxNode = leftMaxNode.right;
               }
               if(target == root){
                   if(leftMaxNode != target.left){
                       leftMaxNode.parent.right = null;
                       leftMaxNode.left = target.left;
                       leftMaxNode.left.parent = leftMaxNode.left;
                   }
                   leftMaxNode.right = target.right;
                   leftMaxNode.right.parent = leftMaxNode;
                   root = leftMaxNode;
                   root.parent = null;
               }
               else{
                   if(leftMaxNode != target.left){
                       leftMaxNode.parent.right = null;
                       leftMaxNode.left = target.left;
                       leftMaxNode.left.parent = leftMaxNode;
                   }
                   leftMaxNode.right = target.right;
                   leftMaxNode.right.parent = leftMaxNode;
                   leftMaxNode.parent = target.parent;
                   if(target == target.parent.left){
                       target.parent.left = leftMaxNode;
                   }else{
                       target.parent.right = leftMaxNode;
                   }
               }
               target.parent = target.left = target.right = null;
            }
        }
    }

    public List preIterator(SortedBinTree5.Node node){
        List list = new ArrayList<>();
        list.add(node);
        if(node.left!=null){
            list.addAll(preIterator(node.left));
        }
        if(node.right!=null){
            list.addAll(preIterator(node.right));
        }
        return list;
    }

    public List inIterator(SortedBinTree5.Node node){
        List list = new ArrayList<>();
        if(node.left!=null){
            list.addAll(inIterator(node.left));
        }
        list.add(node);
        if(node.right!=null){
            list.addAll(inIterator(node.right));
        }
        return list;
    }

    public List postIterator(SortedBinTree5.Node node){
        List list = new ArrayList<>();
        if(node.left!=null){
            list.addAll(postIterator(node.left));
        }
        if(node.right!=null){
            list.addAll(postIterator(node.right));
        }
        list.add(node);
        return list;
    }

    public List breadthIterator(SortedBinTree5.Node node){
        List nodeList = new ArrayList<>();
        Queue queue = new ArrayDeque<>();
        if(node!=null){
            queue.offer(node);
        }
        SortedBinTree5.Node cur = null;
        while (!queue.isEmpty()){
            nodeList.add(queue.peek());
            cur = queue.poll();
            if(cur.left != null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
        }
        return nodeList;
    }
}

代码如上。

主要讲解一下删除节点的思路，总的指导思想就是建立新节点的父子关系，断开目标节点的父子关系。

1. 确定要删除的目标节点的替代节点。有不同的思路，最常用的有最大左子节点替代法与最小右子节点替代法。这两种方法可自行百度一下，此处不再赘述。本文采用最大左子节点替代法，该节点记灵leftMaxNode.
2. 查找到要删除的目标节点：记为target。
3. 找到目标节点的最大左子节点：记为leftMaxNode.
4. 进行目标节点的删除及对leftMaxNode节点建立新的父节点及左右子节点的关系。详细过程如下： 
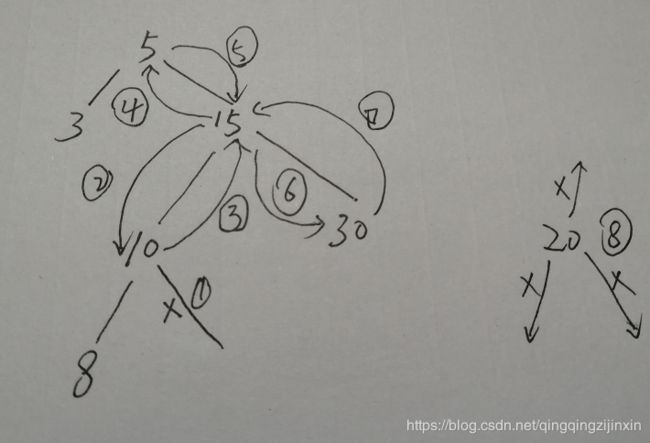
   1. 断开leftMaxNode节点与原父节点关系：leftMaxNode.parent.right = null; 这一步有个条件，if(leftMaxNode != target.left)，leftMaxNode不是目标节点左子节点。也就是说目标节点的左子节点是一棵完整的二叉树。如图所示，节点20就要删除的目标节点，其左子树是一棵完整的二叉树。 leftMaxNode是节点15.                                                                                        图示：
   2. 建立节15的左子节点，即target节点左子节点： leftMaxNode.left = target.left;
   3. 节点15的左子节点的父节点就是节点15：  leftMaxNode.left.parent = leftMaxNode; 前三步的完整代码如下：

                         if(leftMaxNode != target.left){
                             leftMaxNode.parent.right = null;
                             leftMaxNode.left = target.left;
                             leftMaxNode.left.parent = leftMaxNode;
                         }

       

   4. 建立节点15的父节点关系，节点15的父节点指向target节点的父节点： leftMaxNode.right = target.right;
   5. 对节点15的新父节点，建立其与节点15的关系，此时要进行判断节点15是新父节点左子节点还是右子节点，第4步与第5步代码：     

                     leftMaxNode.parent = target.parent;
                         if(target == target.parent.left){
                             target.parent.left = leftMaxNode;
                         }else{
                             target.parent.right = leftMaxNode;
                         }

                       
   6. 建立节点15与右子节点的关系，leftMaxNode.right = target.right;
   7. 建立节点15的右子节点的父节点的关系： leftMaxNode.right.parent = leftMaxNode;
   8. 最后断开target节点的父节点及左右子节点的关系：  target.parent = target.left = target.right = null;

整个过程如图所示(用笔画图比较快，请不要笑话)，大家可以照着画一下图，方便理解：