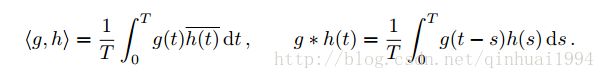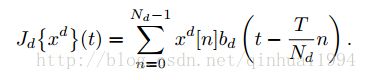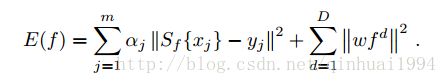【目标跟踪】C-COT：Beyond Correlation Filters: Learning Continuous Convolution Operators for VisualTracking

本文参考文献Beyond Correlation Filters: Learning Continuous
Convolution Operators for Visual Tracking

作为近来大热的ECO的前作，很奇怪博主在网上却没有找到一篇解读它的文章，所以花了点功夫，把我理解的C-COT算法写了下来，文章仍有很多不足，希望可以和大家交流交流~

符号标注

定义了傅里叶系数

ĝ[k]=<g,ek> g ^ [ k ] =< g , e k >

任何 g∈L2(T) g ∈ L 2 ( T ) 可以表示为傅里叶级数形式：

L2(T) L 2 ( T ) 表示勒贝格可积空间

xj x j 表示训练样本

x1j...xDj x j 1 . . . x j D 表示来源于样本 xj x j 的D个特征

Nd N d 表示特征 xdj x j d 的空间样本数量，即 xdj∈RNd x j d ∈ R N d

xdj x j d 中的第n个参数由 xdj[n] x j d [ n ] 表示

所以，样本空间可表示为:

χ=RN1×...×RND χ = R N 1 × . . . × R N D

建立方程

为了简便，公式的推到在一维空间进行，在后续的章节将会向高维空间进行拓展。
文中针对在连续空间域中构建学习问题，对训练样本建立了一个插值模型（implicit interpolation model ），对每个特征通道d，文中定义了一个插值算子， Jd J d :

插值函数 Jd(xd)(t) J d ( x d ) ( t ) 实际上可以视为插值函数 bd b d 平移之后叠加形成的函数，特征通道d中第n维的特征值 xd[n] x d [ n ] 可看作相应位移函数的权值。

注：我个人认为这个插值函数的意义是将某一特征通道内离散的数据拟合成连续函数，连续的意义在后面可以体会到。

如之前讨论的一样，文章的目标是学习到一个线性卷积算子（映射） Sf:χ→L2(T) S f : χ → L 2 ( T ) 这个算子可以将样本空间 χ χ 内的样本 x 映射到目标置信函数 s(t)=Sf(x)(t) s ( t ) = S f ( x ) ( t ) ， s(t) s ( t ) 是目标在位置t的置信度得分。那么对应最大 s(t) s ( t ) 所在的位置t就是目标所在的位置。

在文中，算子 Sf S f 由由一组卷积滤波器 f=(f1...fD)∈L2(T)D f = ( f 1 . . . f D ) ∈ L 2 ( T ) D 参数化。 fd f d 是特征通道d的连续滤波器，所以，可以定义卷积算子如下：

在公式中，每一个特征通道d先用 Jd J d 算子进行插值，然后与相应的滤波器进行卷积。由于是在连续域进行的计算，所以可以得到比离散的像素点更精确的解。

假设有m个训练样本 (xj,yj)m1⊂χ×L2(T) ( x j , y j ) 1 m ⊂ χ × L 2 ( T ) ,其中 yj y j 是算子 Sf S f 应用在样本 xj x j 上的期望输出，那么卷积滤波器 f=(f1...fD)∈L2(T)D f = ( f 1 . . . f D ) ∈ L 2 ( T ) D 可通过最小化一下方程得到：

其中 αj α j 表示训练样本j对整体的影响程度。

注：

论文的3.3节是针对连续滤波器 f f 的求解的推导过程，大体意思是将时域的计算转化到复频域，从而简化计算。具体的过程还没看太清楚，以后补充。

期望输出 yj y j 和插值函数 bd b d 的选取

yj y j 是一个高斯分布，中心在目标点处
插值函数 bd b d 是三次样条插值核 b(t) b ( t ) 的函数,是插值核 b(t) b ( t ) 的位移后的叠加

拓展到高维

对于二维图像，文中使用两个变量 g(t1,t2) g ( t 1 , t 2 ) 的平方可积分周期函数的空间 L2(T1,T2) L 2 ( T 1 , T 2 )
对于期望输出 yj y j 可以直接用二维高斯分布表示。
插值函数则可由三次样条插值函数的分离组合直接表示： b(t1,t2)=b(t1)b(t2) b ( t 1 , t 2 ) = b ( t 1 ) b ( t 2 )