扩展欧几里德算法与数论倒数

欧几里德算法是一个很古老但很有效的计算最大公约数的算法。这个算法很简单，用C++代码来表示就是：

int gcd(int a, int b)
{
    while(b != 0)
    {
        int c = a;
        a = b;
        b = c % b;
    }
    return a;
}

可以证明，对于给定的任意两个整数a和b，总是存在整数s和t，使得他们的最大公约数gcd(a, b)满足以下等式：

as+bt=gcd(a,b)

欧几里得算法只是单纯地求出gcd(a, b)，而扩展欧几里得算法还可以求出等式中的整数s和t。
那求出的s和t有什么作用呢？
我们知道，密码学中经常会碰到需要求某个数a在模b下的数论倒数。也就是求满足下列等式的整数s

as+bt=1

实际上如果a和b互质，则gcd(a, b)=1，那么 as+bt=gcd(a,b)可以转换为上式。
也就是说，扩展欧几里得算法可以用来计算数论倒数。

扩展欧几里德算法有递归跟非递归两种实现，这里我们介绍非递归形式的实现。

要以迭代的形式实现扩展欧几里德算法，关键是写出s和t的递推式。下面为了方便起见，我们假设a总是大于b的。
在欧几里德算法的迭代实现中，倒数第二次循环后我们就可以得到b = gcd(a, b)（最后一次循环是把b的值赋给a，返回a作为最终结果）。假设我们在每一次的循环中，都可以把b表示为

bi=a0si+b0ti，a0跟b0是指变量a和b的初始值

的形式，那么在倒数第二次循环后，我们就可以得到满足下式的s和t

gcd(a0,b0)=a0s+b0t

下面我们先直接给出b的递推公式：

bi=bi−2−⌊ai−1/bi−1⌋bi−1

为了方便表示，我们令 qi−1=⌊ai−1/bi−1⌋，则式子为

bi=bi−2−qi−1bi−1

要把这条公式改写成关于s和t的递推式，只要把

bi−1=a0si−1+b0ti−1

bi−2=a0si−2+b0sti−2

代入式中，即得：

bi=(si−2−qi−1si−1)a0+(ti−2−qi−1ti−1)b0

最终我们得到了s和t的递推式

si=si−2−qi−1si−1(i>1),s0=1,s1=0

ti=ti−2−qi−1ti−1(i>1),t0=0,t1=1

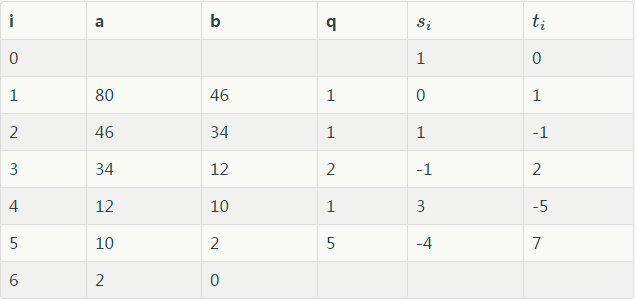
下面是利用扩展欧几里德算法求方程 80∗s+46∗t=gcd(80,46)的解。

表格中倒数第二行中的-4跟7就是我们需要的结果。也就是−4×80+7×46=2=gcd(80,46)

在RSA算法中，扩展欧几里德算法用来求e在模φ(n)下的数论倒数，也就是求方程

de+kϕ(n)=gcd(e,ϕ(n))=1

中 d的值，也就是上面递推式中的 t。
利用上面推导出的递推公式，可以很容易地写出完整的代码。

下面是求数论倒数的C++实现：

int invert(int e, int f)
{
	int a = f, b = e, t1 = 0, t2 = 1;
	
	while(b != 0)
	{
		int t = a;
		a = b;
		int q = t / b;
		b = t % b;
		
		t = t1 - q * t2;
		t1 = t2;
		t2 = t;
	}
	
	if(t1 < 0)  //扩展欧几里得算法得到的结果可能为负数，所以需要把它“掰正”
		t1 += f;
	return t1;
}

下面是基于GMP实现的支持大整数运算的代码：

void invert(mpz_t rop, mpz_t e, mpz_t f)
{
	mpz_t a, b, t1, t2, t, q;
	mpz_init_set(a, f);  //a = f
	mpz_init_set(b, e);  //b = e
	mpz_init(t1);            //t1 = 0
	mpz_init_set_ui(t2, 1);  //t2 = 1
	mpz_init(t);
	mpz_init(q);

	while(mpz_cmp_ui(b, 0) != 0) //b != 0
	{
		mpz_set(t, a);  //t = a
		mpz_set(a, b);  // a = b
		mpz_fdiv_qr(q, b, t, b); 
		//q = t / b, b = t % b
		
		mpz_mul(t, q, t2);
		mpz_sub(t, t1, t);  //t = t1 - q * t2
		
		mpz_set(t1, t2); //t1 = t2
		mpz_set(t2, t);  //t2 = t
	}
	if(mpz_cmp_ui(t1, 0) < 0)
		mpz_add(t1, t1, f);
	mpz_set(rop, t1);	
}