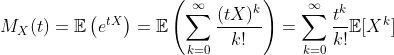R语言蒙特卡洛计算和快速傅立叶变换计算矩生成函数
原文链接:http://tecdat.cn/?p=13734
对精算科学来说,当我们处理独立随机变量的总和时,特征函数很有趣,因为总和的特征函数是特征函数的乘积。
-
介绍
在概率论中,让 ![]() 对于
对于 ![]() 和
和 ![]() 对于
对于 ![]() 是一些随机变量的累积分布函数
是一些随机变量的累积分布函数 ![]() ,即
,即 ![]() 。什么是矩生成函数
。什么是矩生成函数 ![]() ,即
,即 ![]() ?
?
如何编写 ![]() ?
?
在概率教科书中,标准答案是
- 如果
 是离散的
是离散的
- 如果
 (绝对)连续,
(绝对)连续,
![]() 是的密度
是的密度 ![]() 。这里,
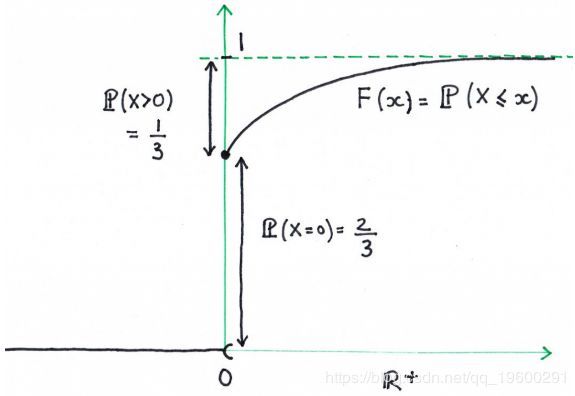
。这里, ![]() 显然不是离散变量。但是是连续的。需要绘制该分布函数以查看,
显然不是离散变量。但是是连续的。需要绘制该分布函数以查看, ![]() , 对所有
, 对所有 ![]()
我们有一个不连续的0。因此,我们在这里必须谨慎一些: ![]() 既不是连续的也不是离散的。让我们使用公式,
既不是连续的也不是离散的。让我们使用公式,
![]()
如果也可以写 ![]() ,
,
![]()
这只是说总体平均值是每个子组平均值的重心。![]() 然后让
然后让 ![]() 而
而 ![]()
![]() )。
)。
![]()
让我们考虑三个不同的组成部分。
![]()
![]()
![]()
(因为它是一个实值常量),在这里 ![]() 。
。
所以最后,我们计算 ![]() 。观察一下
。观察一下 ![]() 给定
给定 ![]() 是具有密度的(绝对)连续随机变量。观察所有
是具有密度的(绝对)连续随机变量。观察所有 ![]() ,
,
和 ![]() ,即
,即 ![]() 给定
给定 ![]() 是指数分布。
是指数分布。
因此, ![]() 是指数变量和Dirac质量之间的混合
是指数变量和Dirac质量之间的混合 ![]() 。这实际上是问题的棘手部分,因为当我们看到上面的公式时,它并不明显。
。这实际上是问题的棘手部分,因为当我们看到上面的公式时,它并不明显。
从现在开始,这是高中阶段的计算,
如果 ![]() 。如果把所有的放在一起
。如果把所有的放在一起
- 蒙特卡洛计算
可以使用蒙特卡洛模拟来计算该函数,
> F=function(x) ifelse(x<0,0,1-exp(-x)/3)
> Finv=function(u) uniroot(function(x) F(x)-u,c(-1e-9,1e4))$root或(以避免不连续的问题)
> Finv=function(u) ifelse(3*u>1,0,uniroot(function(x)
+ F(x)-u,c(-1e-9,1e4))$root))在这里,逆很容易获得,因此我们可以使用
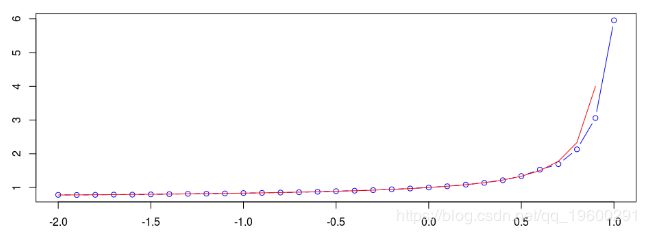
然后,我们使用
> plot(u,v,type="b",col='blue')
> lines(u,Mtheo(u),col="red")
蒙特卡洛模拟的问题在于,仅当它们有效时才应使用它们。我可以计算
> M(3)
[1] 5748134有限总和始终可以通过数字计算。就算在这里 ![]() 不存在。就像Cauhy样本的平均值一样,即使期望值不存在,我也总是可以计算出来
不存在。就像Cauhy样本的平均值一样,即使期望值不存在,我也总是可以计算出来
> mean(rcauchy(1000000))
[1] 0.006069028这些生成函数在存在时会很有趣。也许使用特征函数是一个更好的主意。
- 生成函数
首先,让我们定义那些函数。
![]()
如果 ![]() 足够小。
足够小。
现在,如果我们使用泰勒展开式
和
如果我们看一下该函数在0点的导数的值,那么
可以为某些随机矢量在更高维度上定义一个矩生成函数 ![]() ,
,
![]() 如果要导出给定分布的矩,则一些矩生成函数很有趣。另一个有趣的特征是,在某些情况下,此矩生成函数(在某些条件下)完全表征了随机变量的分布。
如果要导出给定分布的矩,则一些矩生成函数很有趣。另一个有趣的特征是,在某些情况下,此矩生成函数(在某些条件下)完全表征了随机变量的分布。 ![]() ,
,![]() 对所有人
对所有人 ![]() , 然后
, 然后 ![]() 。
。
- 快速傅立叶变换
回想一下欧拉公式,
![]()
因此,看到傅立叶变换就不会感到惊讶。从这个公式,我们可以写
![]()
使用傅立叶分析中的一些结果,我们可以证明概率函数满足
也可以写成
如果在点处的分布是绝对连续的,则可以获得类似的关系 ![]() ,
,
实际上,我们可以证明,
然后可以使用1951年获得的吉尔-佩莱阿兹(Gil-Peleaz)的反演公式来获得累积分布函数,
这意味着,在金融市场上工作的任何人都知道用于定价期权的公式(例如,参见 Carr&Madan(1999) )。好处是,可以使用任何数学或统计软件来计算这些公式。
- 特征函数和精算科学
对精算科学来说,当我们处理独立随机变量的总和时,特征函数很有趣,因为总和的特征函数是特征函数的乘积。考虑计算Gamma随机变量复合和的99.5%分位数的问题,即
![]() 和
和 ![]() 。策略是分散损失金额,
。策略是分散损失金额,
然后,要计算的代码 ![]() , 我们用
, 我们用
99.5%分位数
> sum(cumsum(f)<.995)考虑以下损失金额
> print(X[1:5])
[1] 75.51818 118.16428 14.57067 13.97953 43.60686让我们拟合一个伽玛分布。我们可以用
shape rate
1.309020256 0.013090411
(0.117430137) (0.001419982)
> alpha
[1] 1.308995
> beta
[1] 0.01309016无论如何,我们都有个人损失的Gamma分布参数。并假设泊松计数变量的均值为
> lambda <- 100同样,可以使用蒙特卡洛模拟。我们可以使用以下通用代码:首先,我们需要函数来生成两种感兴趣的变量,
如果我们生成一百万个变量,我们可以得到分位数的估算,
> set.seed(1)
> quantile(rcpd4(1e6),.995)
99.5%
13651.64另一个想法是记住Gamma分布的比例:独立Gamma分布的总和仍然是Gamma(在参数上有附加假设,但在此我们考虑相同的Gamma分布)。因此,可以计算复合和的累积分布函数,
如果我们求解那个函数,我们得到分位数
> uniroot()$root
[1] 13654.43这与我们的蒙特卡洛计算一致。现在,我们也可以在此处使用快速傅立叶变换,
> sum(cumsum(f)<.995)
[1] 13654让我们比较获得这三个输出的计算时间
> system.time
user system elapsed
2.453 0.106 2.611
> system.time
user system elapsed
0.041 0.012 0.361
> system.time
user system elapsed
0.527 0.020 0.560