Pixel-wise orthogonal decomposition for color illumination invariant and shadow-free image

原文：【Qu L, Tian J, Han Z, et al. Pixel-wise orthogonal decomposition for color illumination invariant and shadow-free image[J]. Optics express, 2015, 23(3): 2220-2239.】

Abstract：
本文提出的shadow removal方法，基于阴影不变量的物理基础，对于每一个像素值矢量，建立一个线性方程组，然后推断出像素级的正交分解以求解方程，最终得到一个唯一的光照不变矢量。根据该不变量和Lab颜色空间，本文提出了生成无阴影的彩色图像，并且能够较好的保留纹理和颜色信息。

Introduction：
本算法主要思路为：
1.通过前面的工作（后面会描述）中定义的阴影线性模型，可得到三个不同的光照不变的灰度图。利用该灰度图，对于每个像素点建立一个由三个线性方程组成的线性方程组；
2.求解线性方程组。线性方程的解空间被分解为一维零空间和特定解空间（particular solution space）。零空间只和光照条件有关，特定解空间则和光照无关了。
3.由实验可知，得到的彩色光照不变图像会存在颜色失真的问题，因此，再结合Lab颜色空间，对其进行处理，就能够产生一个无阴影的彩色图像，并且能够较好保留颜色和纹理信息。

算法详细介绍：
2.1 像素级正交分解
2.1.1 基于前面的工作^[1]获取的阴影线性模型
对于一定范围内的可见光，在给定光照的光谱功率分布（SPD）E（λ），目标反射率S（λ），和相机传感器响应Q（λ）的情况下，相机的响应值（即最终得到的像素值）如下：
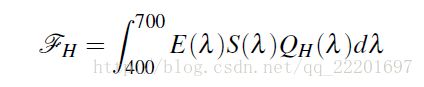（1）
太阳发出的光线经过大气透射的影响，到达地面的入射光就被分为了直射的太阳光（sunlight）和漫反射的天空光（skylight）。对于阴影区域来说，得到的光线只有天空光，而非阴影区域则还包括太阳光。在比较容易出现阴影的晴朗天气，日光（太阳光和天空光的结合）和环境光（天空光）有着强烈的规律性，主要是由太阳角度控制的。基于上述准则，对于同一表面来说，在不同光照下相机响应的像素值的每个通道满足如下规则：
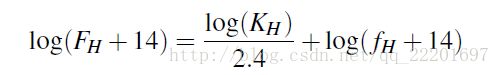（2）
H代表通道标号。F_H表示的是非阴影区域的RGB像素值，f_H表示的是相同表面在阴影情况下表现出来的像素值。比例系数K_H与表面反射率无关，近似等于下式决定的常数：
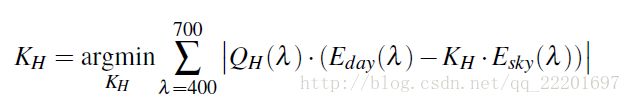（3）
这里的E_day和E_sky分别表示日光和环境光下的光谱功率分布。在作者的实验中，这两个SPD是通过统计十个晴天日子里的不同太阳角度下的日光和环境光的SPD，然后计算其均值得到的。上式的步长设置为5nm，K_H的步长设置为0。01，K_H的优化问题可解。
由上面的式（2），可以得到下面的等式成立：
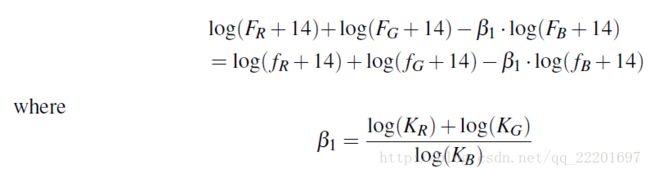（4）

对于图像中的像素点，上式说明了一个阴影不变性。对于任意像素点，对其RGB三个通道的像素值做运算：，则这里不管RGB的值是否是处于阴影下，那么得到的值是相同的，也就是说，和阴影无关了。因此，由此可以得到一个光照无关的灰度图。如下图例所示：

2.1.2像素级正交分解
但是，由于颜色和对比度的损失，在许多应用中，上述光照不变的灰度图存在很多局限性。因此，希望能够获取一个彩色图像，颜色和纹理尽量和原图保持一致，但是将阴影去除。因此，基于前面的部分，本文推导出了其正交分解，并且获取了一个能够保持基本颜色信息的光照不变图像。

对于一个RGB像素矢量来说，首先根据下式定义如下的一个不变量I₁：
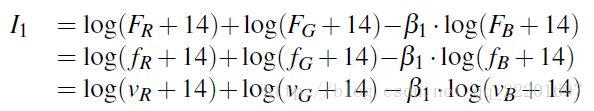（5）
同样，对于另外两幅光照不变的灰度图，可以定义不变量I₂和I₃：
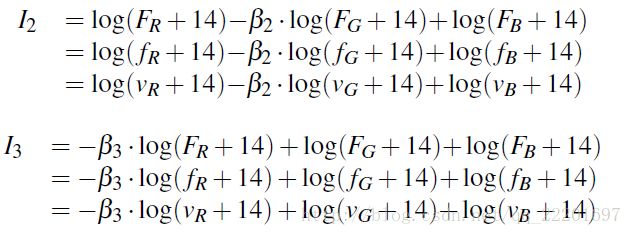（6）
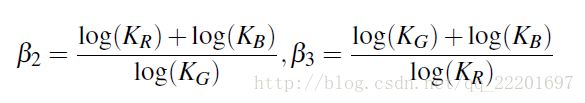这里（9）

为了方便表示，下面用来表示一个RGB像素投影至需要的log空间之后对应的矢量，即这里。因此，公式（5），（6）就可以用下列线性方程组来表示：
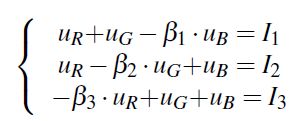（10）
式（10）的矩阵形式如下：
（11），
这里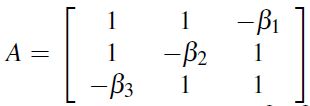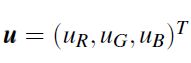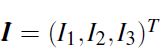，，，。根据β₁，β₂和β₃的定义和计算，可以得到如下关系：
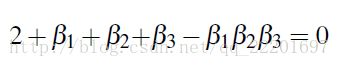（12）

由上述参数之间的关系，可以得到A矩阵的秩等于2。因此，对于给定图像，公式10的解有无限个。该解空间可以被分解为一个特定的解和一个一维零空间解。对于一幅图像中的一个像素点，我们首先就已经得到了一组满足上式的解了，即原RGB像素值的log下取值。因此，我们的目标是找到公式10的一个接，能够满足光照不变。下面，证明该解存在并且唯一。

根据代数原理，对于公式10的任意一个解u，可以用下面的式子表示：
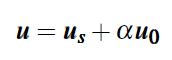（13）
这里u_s为任意特定解，u₀为公式10的归一化的free solution.（这边我理解的是，u₀和u_s是公式10的解空间的一组基向量，只不过在表示空间内的其他向量时，u_s的方向上不加系数，只是变换u₀的系数。）而u₀作为公式10的free solution，是满足Au₀=0的，并且||u₀||=1。
其中一个free solution的值如下：
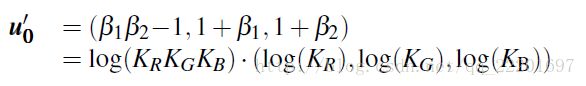（14），
归一化之后可得u₀为：
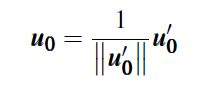（15）
由公式13可以看出，free solution u₀和图像本身没有关系，而是由矩阵A决定的，也就是说，是由光照决定的。

对于上面的定义，给定一个特定解u_s和一个归一化之后的free solution u₀，根据公式13和代数相关理论，就可以定义u_p如下：
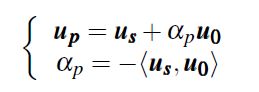（16）
如此，u_p就是方程11的一个解。< , >表示向量内积。可以证明，u_p⊥u₀，是方程11的唯一特定解。

根据上面的推导，给定一幅在不同光照下拍摄所得的图像，对于每个像素点对应的log-RGB值的矢量u，可以直接计算出其对应的光照不变量u_p，如下：
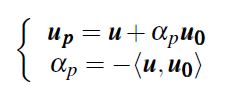（17）
再对其去exp，就可以回到三维RGB颜色空间。

对于给定像素，不管由于不同光照带来的颜色变化有多大，该正交分解过程能够获得唯一的u_p。
分解原理课如下理解：

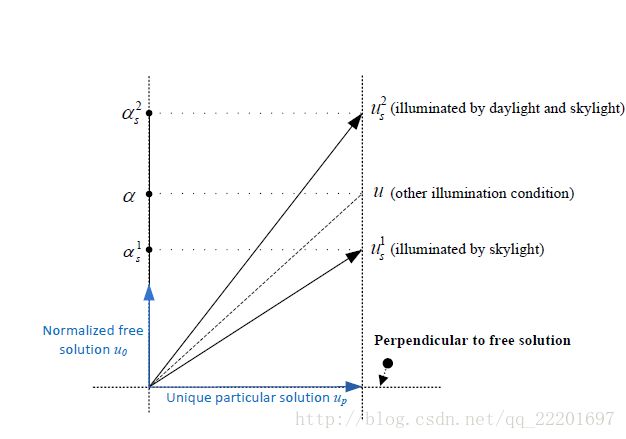
2.2 参数β₁，β₂，β₃的分析获取以及彩色光照不变图像的获取
参数β₁，β₂，β₃直接影响着不变量的获取，由于β₁，β₂，β₃是和光照有关，因此作者通过统计实验，获取不同天气以及太阳角度下的数据，得到了β₁，β₂，β₃的结果，实验给定均值可以用于多种情况下。

3.颜色还原
通过对于中性颜色的处理，以及投影至Lab颜色空间，最终得到无阴影的彩色图像。

[1]Tian J, Tang Y. Linearity of each channel pixel values from a surface in and out of shadows and its applications[C]//Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE, 2011: 985-992.