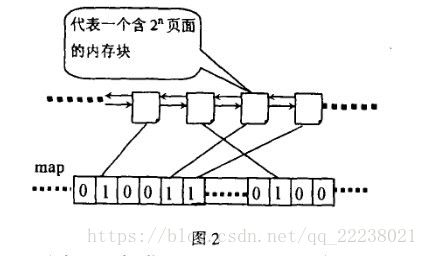
伙伴(buddy)算法及位图
伙伴(buddy)算法,它不能根据需要从被管理内存的开头部分创建新内存。它有明确的共性,就是各个内存块可分可合,但不是任意的分与合。每个块都有个朋友,或叫“伙伴”,既可与之分开,又可与之结合。伙伴分配程序把内存块存放在比链接表更先进的数据结构中。这些结构常常是桶型、树型和堆型的组合或变种。一般来说,伙伴分配程序的工作方式是难以描述的,因为这种技术随所选数据结构的不同而各异。由于有各种各样的具有已知特性的数据结构可供使用,所以伙伴分配程序得到广泛应用。有些伙伴分配程序甚至用在源码中。伙伴分配程序编写起来常常很复杂,其性能可能各不相同。伙伴分配程序通常在某种程度上限制内存碎片。
伙伴算法管理的是物理内存。
伙伴算法作用:
通常情况下,一个高级操作系统必须要给进程提供基本的、能够在任意时刻申请和释放任意大小内存的功能,就像malloc 函数那样,然而,实现malloc 函数并不简单,由于进程申请内存的大小是任意的,如果操作系统对malloc 函数的实现方法不对,将直接导致一个不可避免的问题,那就是内存碎片。
内存碎片就是内存被分割成很小很小的一些块,这些块虽然是空闲的,但是却小到无法使用。随着申请和释放次数的增加,内存将变得越来越不连续。最后,整个内存将只剩下碎片,即使有足够的空闲页框可以满足请求,但要分配一个大块的连续页框就可能无法满足,所以减少内存浪费的核心就是尽量避免产生内存碎片。针对这样的问题,有很多行之有效的解决方法,其中伙伴算法被证明是非常行之有效的一套内存管理方法,因此也被相当多的操作系统所采用。
伙伴算法(Buddy system)把所有的空闲页框分为11个块链表,每块链表中分布包含特定的连续页框地址空间,比如第0个块链表包含大小为2^0个连续的页框,第1个块链表中,每个链表元素包含2个页框大小的连续地址空间,….,第10个块链表中,每个链表元素代表4M的连续地址空间。每个链表中元素的个数在系统初始化时决定,在执行过程中,动态变化。
伙伴算法每次只能分配2的幂次个页框的空间,比如一次分配1页,2页,4页,8页,…,1024页(2^10)等等,每页大小一般为4K,因此,伙伴算法最多一次能够分配4M(1024*4K)的内存空间。
核心概念和数据结构
两个内存块,大小相同,地址连续,同属于一个大块区域。(第0块和第1块是伙伴,第2块和第3块是伙伴,但第1块和第2块不是伙伴)
伙伴位图:用一位描述伙伴块的状态位码,称之为伙伴位码。比如,bit0为第0块和第1块的伙伴位码,如果bit0为1,表示这两块至少有一块已经分配出去,如果bit0为0,说明两块都空闲,还没分配。
Linux2.6为每个管理区使用不同的伙伴系统,内核空间分为三种区,DMA,NORMAL,HIGHMEM,对于每一种区,都有对应的伙伴算法,
1. free_area数组:
1: struct zone{
2: ....
3: struct free_area free_area[MAX_ORDER];
4: ....
5: }
struct free_area free_area[MAX_ORDER] #MAX_ORDER 默认值为11,分别存放着11个组,free_area结构体里面又标注了该组别空闲内存块的情况。
2. zone_mem_map数组
free_area数组中,第K个元素,它标识所有大小为2^k的空闲块,所有空闲快由free_list指向的双向循环链表组织起来。其中的nr_free,它指定了对应空间剩余块的个数。
整个分配图示,大概如下:
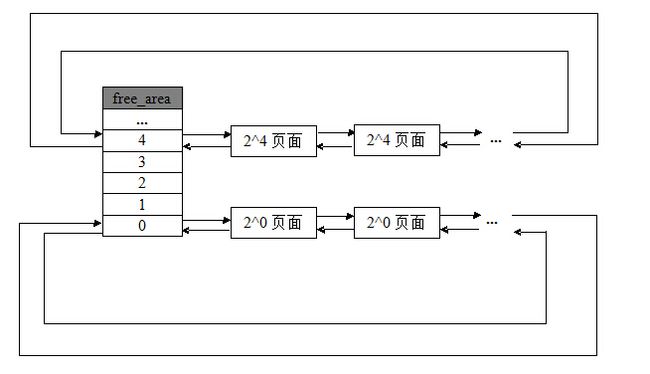
内存分配原理
比如,要分配4(2^2)页(16k)的内存空间,算法会先从free_area[2]中查看nr_free是否为空,如果有空闲块,就直接从中摘下并分配出去,如果没有空闲块,就顺着数组向上查找,从它的上一级free_area[3](每块32K)中分配,如果free_area[3]中有空闲块,则将其从链表中摘下,分成等大小的两部分,前四个页面作为一个块插入free_area[2],后4个页面分配出去,如果free_area[3]也没有空闲,则从更上一级申请空间,如果free_area[4]中有,就将这16(2*2*2*2)个页面等分成两份,前一半挂在free_area[3]的链表头部,后一半的8个页等分成两等分,前一半挂free_area[2]的链表中,后一半分配出去。依次递推,直到free_area[max_order],如果顶级都没有空间,那么就报告分配失败。
内存释放原理(回收内存)
释放是申请的逆过程,也可以看作是伙伴的合并过程。当释放一个内存块时,先在其对于的free_area链表中查找是否有伙伴存在,如果没有伙伴块,直接将释放的块插入链表头。如果有或板块的存在,则将其从链表摘下,合并成一个大块,然后继续查找合并后的块在更大一级链表中是否有伙伴的存在,直至不能合并或者已经合并至最大块2^10为止。
内核试图将大小为b的一对空闲块(一个是现有空闲链表上的,一个是待回收的),合并为一个大小为2b的单独块,如果它成功合并所释放的块,它会试图合并2b大小的块。
关于位图
Linux内核伙伴算法中每个order 的位图都表示所有的空闲块,位图的某位对应于两个伙伴块,为1就表示其中一块忙,为0表示两块都闲或都在使用。系统每次分配和回收伙伴块时都要对它们的伙伴位跟1进行异或运算。所谓异或是指刚开始时,两个伙伴块都空闲,它们的伙伴位为0,如果其中一块被使用,异或后得1;如果另一块也被使用,异或后得0;如果前面一块回收了异或后得1;如果另一块也回收了异或后得0。
位图的主要用途是在回收算法中指示是否可以和伙伴块合并,分配时只要搜索空闲链表就足够了。当然,分配的同时还要对相应位异或一下,这是为回收算法服务。
关于分配算法
假设在初始阶段,全是大小为2^9大小的块( MAX_ORDER为10),序号依次为0, 512, 1024等等,并且所有area的map位都为0(实际上操作系统代码要占一部分空间,但这里只是举例),现在要分配一个2^3大小的页面块,有以下动作:
1. 从order为3的area的空闲链表开始搜索,没找到就向高一级area搜索,依次类推,按照假设条件,会一直搜索到order为9的area,找到了序号为0的2^9页块。
2. 把序号为0的2^9页块从order为9的area的空闲链表中摘除并对该area的第0位( 0>>(1+9) )异或一下得1。
对area的第(序号右移(1+order)的结果)位跟1异或一下
3. 把序号为0的2^9页块拆分成两个序号分别为0和256的2^8页块,前者放入order为8的area的空闲链表中,并对该area的第0位( 0>>(1+8) )异或一下得1。
4. 把序号为256的2^8页块拆分成两个序号分别为256和384的2^7页块,前者放入order为7的area的空闲链表中,并对该area的第1位( 256>>(1+7) )异或一下得1。
5. 把序号为384的2^7页块拆分成两个序号分别为384和448的2^6页块,前者放入order为6的area的空闲链表中,并对该area的第3位( 384>>(1+6) )异或一下得1。
6. 把序号为448的2^6页块拆分成两个序号分别为448和480的2^5页块,前者放入order为5的area的空闲链表中,并对该area的第7位( 448>>(1+5) )异或一下得1。
7. 把序号为480的2^5页块拆分成两个序号分别为480和496的2^4页块,前者放入order为4的area的空闲链表中,并对该area的第15位( 480>>(1+4) )异或一下得1。
8. 把序号为496的2^4页块拆分成两个序号分别为496和504的2^3页块,前者放入order为3的area的空闲链表中,并对该area的第31位( 496>>(1+3) )异或一下得1。
9. 序号为504的2^3页块就是所求的块。
把序号为n的页面块插入order为i的area时,需要对该area的map位(n>>(1+order))跟1异或,更新map值
关于回收算法
1.当回收序号为4的1页块时,先找到order为0的area,把该页面块加入到该area的空闲链表中,然后判断其伙伴块(序号为5的1页块)的状态,读该area (不是其它area !)的map的第2(下标为2 序号右移1+order的结果)位( 4>>(1+order) ),假设伙伴块被占,则该位为0(回收4块前,4、5块都忙),现跟1异或一下得1,并不再向上合并。
2.当回收序号为5的1页块时,同理,先找到order为0的area,把该页面块加入到该area的空闲链表中,然后判断其伙伴块(序号为4的1页块)的状态,读该area的map的第2位(5>>(1+order) ),这时该位为1(先前4块已回收,5块占用),现跟1异或一下得0,并向上合并,把序号为4的1页块和序号为5的1页块从该area的空闲链表中摘除,合并成序号为4的2页块,并放到order为1的area的空闲链表中。同理,此时又要判断合并后的块的伙伴块(序号为6的2页块)的状态,读该area(order为1的area,不是其它!)的map的第1位((4>>(1+order) ),假设伙伴块在此之前已被回收,则该位为1,现异或一下得0,并向上合并,把序号为4的2页块和序号为6的2页块从order为1的area的空闲链表中摘除,合并成序号为4的4页块,并放到order为2的area的空闲链表中。然后再判断其伙伴块状态,如此反复。
回收的页面块假设序号为n,检查order为i的该area中的map[n>>(1+order)],将该map值跟1异或,若结果为0,则序号n的页面块可跟其伙伴块合并,否则不能合并。
回收的页块若能与伙伴块合并,插入上一级的area中,则视合并块为之前已被占用,然后根据该area中其伙伴块的状态(已被回收或者被占用)判断其map位是1(其伙伴块已被回收)还是0(其伙伴块被占用),再让map位跟1异或一下,结果为0则再合并,结果为1则不再合并。map的第几位(下标)判断依据:页块的序号>>(1+order)
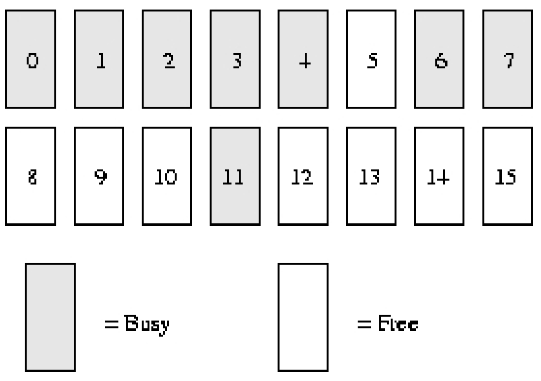
另一个例子(位图的使用):假设我们的系统内存只有16个页面RAM。因为RAM只有16个页面,我们只需用四个级别(orders)的伙伴位图(因为最大连续内存大小为16个页面),如下图所示。(2^4=16)
初始位图:
order(0)中,第一个bit表示开始的2个页面(页面0和页面1均忙,故map位位0),第二个bit表示接下来的2个页面,以此类推。因为页面4已分配,而页面5空闲,故第三个bit为1。
order(1)中,第三个bit是1的原因是一个伙伴完全空闲(页面8和9),和它对应的伙伴(页面10和11)却并非如此。以后回收页面时,可以合并。
分配过程
当我们需要order(1)的空闲页面块时,则执行以下步骤:
1、初始空闲链表为:
order(0): 5, 10 (空闲块为什么不是5、8、9、10、12、13、14、15)
order(1): 8 [8,9] (空闲块为什么不是8[8,9]、12[12,13]、14[14,15])
order(2): 12 [12,13,14,15]
order(3): 无空闲块
2、从上面空闲链表中,我们可以看出,order(1)链表上,有一个(为什么不是3个)空闲的页面块,把它(第一个空闲的块)分配给用户,并从该链表中删除。
3、当我们再需要一个order(1)的块时,同样我们从order(1)空闲链表上开始扫描。
4、若在order(1)上没有空闲页面块,那么我们就到更高的级别(order)上找,order(2)。
5、此时有一个空闲页面块,该块是从页面12开始。该页面块被分割成两个稍微小一些order(1)的页面块,[12,13]和[14,15]。[14,15]页面块加到order(1)空闲链表中,同时[12,13]页面块返回给用户。
6、最终空闲链表为:
order(0): 5, 10
order(1): 14 [14,15]
order(2):
order(3):
回收过程
当我们回收页面11(order 0)时,则执行以下步骤:
1、找到在order(0)伙伴位图中代表页面11的位,计算使用下面公示:
index = page_idx >> (order + 1)
= 11 >> (1 + 0)
= 5
2、检查上面一步计算位图中相应bit的值。若该bit值为1,则和我们临近的,有一个空闲伙伴。Bit5的值为1(注意是从bit0开始的,Bit5即为第6bit),因为它的伙伴页面10是空闲的。
3、现在我们重新设置该bit的值为0,因为此时两个伙伴(页面10和页面11)完全空闲。
4、我们将页面10,从order(0)空闲链表中摘除。
5、此时,我们对2个空闲页面(页面10和11,order(1))进行进一步操作。
6、新的空闲页面是从页面10开始的,于是我们在order(1)的伙伴位图中找到它的索引,看是否有空闲的伙伴,以进一步进行合并操作。使用第一步中的计算公式,我们得到bit 2(第3位)(10>>(1+1))。
7、Bit 2(order(1)位图)同样也是1,因为它的伙伴页面块(页面8和9)是空闲的。
8、重新设置bit2(order(1)位图)的值为0,然后在order(1)链表中删除该空闲页面块。
9、现在我们合并成了4页面大小(从页面8开始[8,9,10,11])的空闲块,从而进入另外的级别。在order(2)中找到伙伴位图对应的bit值(8>>(1+2)),是bit1,且值为1,跟1异或后为0,重置bit1为0,需进一步合并(原因同上)。
10、从oder(2)链表中摘除空闲页面块(从页面12开始),进而将该页面块和前面合并得到的页面块进一步合并。现在我们得到从页面8开始,大小为8个页面的空闲页面块[8,9,10,11,12,13,14,15]。
11、我们进入另外一个级别,order(3)。它的位索引为0,它的值同样为0。这意味着对应的伙伴不是全部空闲的,所以没有再进一步合并的可能。我们仅设置该bit为1,然后将合并得到的空闲页面块放入order(3)空闲链表中。
12、最终我们得到大小为8个页面的空闲块:
Buddy算法的优缺点:
伙伴算法的一大优势是它能够完全避免外部碎片的产生,申请时,伙伴算法会给程序分配一个较大的内存空间,即保证所有大块内存都能得到满足。很明显分配比需求还大的内存空间,会产生内部碎片。所以伙伴算法虽然能够完全避免外部碎片的产生,但这恰恰是以产生内部碎片为代价的。优点:
较好的解决外部碎片问题
当需要分配若干个内存页面时,用于DMA的内存页面必须连续,伙伴算法很好的满足了这个要求
只要请求的块不超过512个页面(2K),内核就尽量分配连续的页面。
针对大内存分配设计。
缺点:
1. 合并的要求太过严格,只能是满足伙伴关系的块才能合并,比如第1块和第2块就不能合并。
2. 碎片问题:一个连续的内存中仅仅一个页面被占用,导致整块内存区都不具备合并的条件
3. 浪费问题:伙伴算法只能分配2的幂次方内存区,当需要8K(2页)时,好说,当需要9K时,那就需要分配16K(4页)的内存空间,但是实际只用到9K空间,多余的7K空间就被浪费掉。
4. 算法的效率问题: 伙伴算法拆分和合并涉及了比较多的计算还有链表和位图的操作,开销还是比较大的,如果每次2^n大小的伙伴块就会合并到2^(n+1)的链表队列中,那么2^n大小链表中的块就会因为合并操作而减少,但系统随后立即有可能又有对该大小块的需求,为此必须再从2^(n+1)大小的链表中拆分,这样的合并又立即拆分的过程是无效率的。
Linux针对大内存的物理地址分配,采用伙伴算法,如果是针对小于一个page的内存,频繁的分配和释放,有更加适宜的解决方案,如slab和kmem_cache等