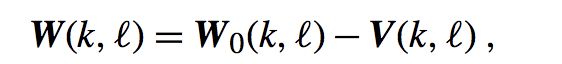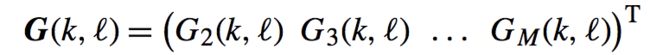频域GSC
之前我讲过LCMV,那么接下来我讲一下GSC算法,他是从LCMV过渡而来。
Griffiths和Jim同样认为每个ATF都是一个简单的时延。他们获得了一个不加约束的自适应算法,同样利用了Frost的约束(意思就是在满足原有约束的条件下设计出了一个不加约束的自适应算法)。相较于约束部分的算法,无约束的算法追踪性能更好,更加稳健。下面我们进入算法部分。
考虑一下我们之前LCMV算法的A的零空间(A是约束条件):
同时考虑一下约束超平面(也就是约束A本身要满足的条件):
这两个平面平行。除此以外,我们定义列空间:
根据我们所学线性代数的知识,我们知道:
同时我们LCMV中的F与N也是垂直的,因为:
它属于列空间R。同时因为:
因此:
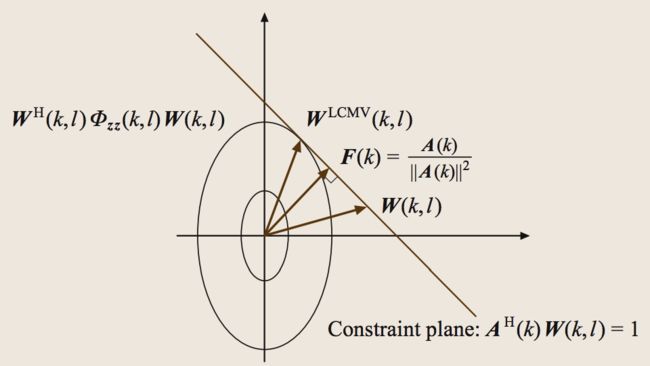
看到这想必很多人已经懵逼了,第一次我看的时候也是懵逼的。我是这么说服我自己的:如果按照点和集合的概念来讲,F确实是在约束平面上的,如下图:
不过如果以向量的形式,从零点到F与平面确实是垂直的关系。所以说二者关系既是属于,又是垂直。
在线性空间中,我们经常把一个线性空间分为两个相互垂直的子空间。所以:
这里:W0属于R,-V属于N。通过定义,我们可以得到:
这里的H是一个矩阵,他的列组成了约束A的零空间。比如:
这里的H就是著名的阻塞矩阵了(BM)。通过阻塞矩阵后的信号通常被我们叫做噪声参考信号U,定义如下:
其中:
可能有些朋友会问,为什么通过阻塞矩阵之后的就是噪声的参考信号了。我简单解释一下,方便后面的继续讲解。首先要明白这个问题,就得先要知道阻塞矩阵顾名思义他阻塞的是什么?通过上面的说明我们知道,阻塞矩阵是约束A的零空间。那么约束A是什么?一个约束,一个指向,一个保留方向保持信号不衰减,没错,约束A代表的是期望信号。那么加入我的观测信号z如下:z=d+n,我们现在把d全部阻塞掉了,那么剩下的就是噪声了(其实是噪声和H的运算结果,暂且不必知道是什么),所以通过H之后我们认为就剩下噪声的参考信号了(至于为什么叫参考,后面会说明)。
还记得上面我们的H后面的G吗,他是秩为:rank{H(k)}*1的向量的自适应滤波器。这里我们假设H的秩为:rank{H}=M-1。因此,滤波器组 被定义为:
从上图Frost中的几何理解来看,我们能确定:
现在我们能得到(我一般这么说,你就不要记怎么推导的,记住下面结论):
其实上面推导的公式中关键的不多,大多是为了理解得到如上的结论。从这个公式开始就是重点,是算法的灵魂,下面我会详细讲解其中每项的含义。约束波束形成的输出包含两部分(一般称为上支路下支路,同时对这里的约束不要有排斥,GSC的思想是基于LCMV思想的,所以整体来看GSC绝对也是约束波束形成期,不过他把约束和自适应分开,达到了解藕的效果,这个后面我们慢慢说),两部分都是对输入信号Z进行操作。其中第一部分,YFBF,仅仅使用一个固定滤波器,所以他可以被认为是一个FBF(Fixed BeamFormer,也就是著名的上支路大人)。FBF对期望信号进行相加,同时能部分减少噪声(Delay and Sum滤波器能力).所以我们一般认为FBF输出的信号的SNR要比输入信号的SNR要大的(那句话怎么讲,蚊子肉虽小,但毕竟是肉)。但是!!!但是!!!但是!!!这个效果很不稳定,所以我们的下支路的身影出现,下面开始讲解下支路,我们经过阻塞矩阵H之后的U表示如下:
之所以上面式子最后的等候右边第一项去掉了是因为H与A是垂直关系,与我之前说的相互验证,剩下的就是H与噪声的运算而已,称之为参考噪声。当然,上面这是比较完美的情况。事实上,H与A的内积并不为0,所以期望信号可能会泄露到参考噪声中去。反之如果能完全阻挡住期望信号,那么剩下的就是如上面式子的噪声信号,所以所以YANC变为了纯噪声项。在YFBF中剩余的噪声可以被自适应滤波器G使用最小输出功率准则去除。这个最小化问题其实就是多通道噪声消除问题。LMS算法被用来处理这种类型问题(LMS不需要过多叙述,上文LCMV已经讲解很清晰明了)。
接下来,我们更加细化,波束形成器包含三部分:上支路的固定波束形成器FBF W0,保留期望信号部分。下支路的阻塞矩阵BM H,用来阻塞期望信号部分,然后产生了噪声参考信号U。最后是一个多通道ANC G,消除因为FBF的旁瓣泄露过去的稳态信号!!!稳态信号!!!稳态信号!!!所以GSC或者说D-GSC对于稳态信号效果很好,非稳态,效果并不理想,比如语音,所以,多人说话情景用GSC几乎没什么效果的。
自适应噪声消除
参考噪声信号被ANC强调同时从FBF的输出中减去,产生如下:
我们给出三个假设:H0s,H0t和H1分别表示滤波器的输出信号中没有瞬变,干扰瞬变,期望信号瞬变。对于滤波器G的最优解是在稳态噪声的情况下(H0s)最小化波束形成器的输出功率。同时记住,当噪声存在瞬变的情况时(比如一个经过的车辆),我们不进行更新操作。当噪声源是固定的,并且噪声的统计特性缓慢变化,ANC滤波器可以追踪其变化。
我们让:
表示输入的稳态噪声的功率谱密度(PSD)。所以,波束形成器的输出功率的最小化是通过解决如下的非约束最优问题来得到的:
这个式子其实就是E[YY*],没有什么可说的,把这个式子看作是代价函数。如果看过我的LCMV算法的,一定对这种式子很有感觉,首先,先求出式子的最优维纳解,就是求导为零等操作或者干脆使用维纳霍夫方程进行推导,我们可以得到(篇幅关系,不进行推导):
不过最优维纳解是理论最优解,我们需要使用随机梯度下降算法的产物LMS算法进行自适应更新G,为了增强稳定性,我们一般使用NLMS算法进行更新,如下:
 后面的Pest表示噪声参考信号的功率,ug是管理收敛速度的步长,ap是PSD估计过程的平滑因子(在你写程序的时候,这些都是几个参数,不过确实有着大作用,千万不要小看,如果是在不知道选多少,查看作者原文里面的实验部分,看作者用的多少)。
后面的Pest表示噪声参考信号的功率,ug是管理收敛速度的步长,ap是PSD估计过程的平滑因子(在你写程序的时候,这些都是几个参数,不过确实有着大作用,千万不要小看,如果是在不知道选多少,查看作者原文里面的实验部分,看作者用的多少)。
同时为了使用STFT,我们进一步假设ANC滤波器gm有着时变的有限脉冲响应(FIR)结构:
这里需要注意,冲激响应不是因果,为了允许FBF和ANC分支的相对延迟。为了实现FIR结构,我们滤波器的更新为:
其中第二个公式包含三个步骤:1.把G_hat(上面有波浪线的)转换到时域 2.截取冲激响应长度为[-KL,KR] 3.把结果转换到频域。算法中涉及到的不同滤波操作都是通过overlap和save方法完成的。之前做实验的时候,这里其实很难把握,调节的过程很难发现效果显著效果,这里我的猜测之所以这么做是因为我们的滤波器长度为KL+LR+1,如果超出这个长度,可能其冲激响应会有变化,可能是很大,或者很小,所以剔除掉这些不稳定的点采用如此方法。当然,仅仅是个人想法,如果有确凿证据的大神,可以在下面给出正确答案,老夫先谢过。
最后给出算法的结构图,算法这两天我会抽空写出来放入我的github,地址见我个人资料,感谢。