信息安全-RSA

      综合几位大佬的文章，链接实在是忘了。

（1）简介

SSA = Signature Scheme with Appendix

PSS = Probabilistic Signature Scheme

ES = Encryption Schemes

SSA是填充、封装格式

PSS是私钥签名流程。

ES 是公钥加密流程。

         RSA的加密机制：RSAES-OAEP和RSAES-PKCS1-v1_5，PKCS#1推荐在新的应用中使用RSAES- OAEP，保留RSAES-PKCS#1-v1_5跟老的应用兼容。它们两的区别仅仅在于加密前编码的方式不同，而加密前的编码是为了提供了抵抗各种活动的敌对攻击的安全机制。与对称加密算法DES，AES一样，RSA算法也是一个块加密算法（ block cipher algorithm），总是在一个固定长度的块上进行操作。但跟AES等不同的是，block length是跟key length有关的。

        RSA的签名机制：RSASSA-PSS和RSASSA-PKCS1-v1_5。同样，推荐RSASSA-PSS用于新的应用,而RSASSA-PKCS1-v1_5只用于兼容老的应用。

（2）RSA算法详解

1. 确认n，选择两个互质的数p=61，q=53，n=p*q=3233，φ(n)=60*52=3120；
2. 确认e，1
3. 确认d，e*d%φ(n)=1；(n,e)为公钥，(n,d)为私钥；

         本质在于，即使你知道了n，但是只要保证n足够大，就算你知道了n，在不知道p和q的情况下你也求不出φ(n)。

加密：假设发送方向接收方发送信息m，m未加密，我们称之为明文。发送方从接收方获得的公钥为(n,e)，加密公式为me=c(mod n)其中，m必须是整数，而且m必须比n小。　m,e,n已知，从上面的公式中计算出c，c就是加密后的信息，我们称之为密文。发送方将密文发送给接收方。

解密：接收方从发送方接收到密文c，用自己的配对私钥(n,d)进行解密，解密公式为cd=m(mod n)已知c,n,d，从上面公式中计算出m，就是发送方发过来的明文；

缺点： 产生密钥麻烦，受到素数产生技术限制，很难做到一次一密；速度太慢，比DSA最低差两个数量级，由于RSA分组长度太大，n至少为600位，使得运算代价很高；

（3）填充算法

1. OAEP= Optimal Asymmetric Encryption Padding
2. PSS = Probabilistic Signature Scheme

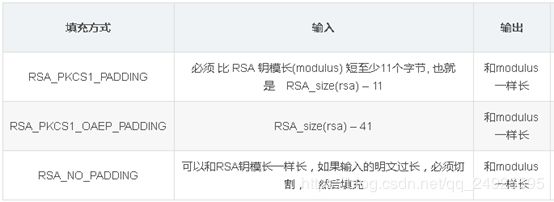
        RSA加密常用的填充模式有三种：RSA_PKCS1_PADDING， RSA_PKCS1_OAEP_PADDING， RSA_NO_PADDING。签名和加密的填充主要是出于安全性考虑：

1： 例如TLS流程中的RSA公钥加密（client key exchange），client会使用随即算法生成2+46=48字节的pre_master_key。 若不进行填充而直接加密，那么显然相同的pre_master_key，会得到相同的密文。这种在语义上来说，是不安全的。

2： 加密流程

加密方加密m：c = m^e mod n，传输c

解密方解密c：m = c^d mod n，还原m

由于c在网络上传输，如果网络上有人对其进行c' = c*k^e mod n，这样的替换那么解密方得到的结果是

(c*k^e)^d mod n  = c^d mod n * k^ed mod n  = m*k

即中间人有办法控制m。

（4）RSAES-PKCS1-v1_5 加密流程

EM = 0x00 || 0x02 || PS || 0x00 || M

作用：RSA公钥加密

加密过程：

1：待加密数据为M，规范要求M必须不大于k-11，其中k是模数n的字节数。

2：若1满足，则计算不存在字节0的随机值PS，显然根据下面的等式可以推算出，PS的长度是 k - M_len - 3

EM = 0x00 || 0x02 || PS || 0x00 || M

EM作为RSA运算的底数M，进行运算。C = EM ^e mod n；

解密过程：

1：校验C的长度，C必须是k字节长度。

2：C ^d mod n得到EM

EM理论上是0x00 || 0x02 || PS || 0x00 || M这种格式的，所以校验的方法也相对比较简单。

先判断开头2字节是否是0x00 0x02，然后找到第一个0x00，这个0x00后面的值就是解密后的明文。

（5）RSASSA-PKCS1-V1_5-SIGN签名流程

EM = 0x00 || 0x01 || PS || 0x00 || T

该签名流程，使用了EMSA-PKCS1-v1_5 封装格式；

1：计算M的哈希值，H = hash(M)，哈希可能是MD5、SHA1、SHA2等算法。

2：H并不会简单的进行模幂运算，而是需要进行封装后才会进行，它需要ASN1编码，下面段数据T的数据组织(OID指的具体HASH算法的id，oid_size表示这个id的长度)

p = T

*p++ = ASN1_SEQUENCE | ASN1_CONSTRUCTED;

*p++ = (unsigned char) ( 0x08 + oid_size + hashlen );

*p++ = ASN1_SEQUENCE | ASN1_CONSTRUCTED;

*p++ = (unsigned char) ( 0x04 + oid_size );

*p++ = ASN1_OID;

*p++ = oid_size & 0xFF;

*memcpy( p, oid, oid_size );

*p += oid_size;

*p++ = ASN1_NULL;

*p++ = 0x00;

*p++ = ASN1_OCTET_STRING;

*p++ = hashlen;

*memcpy( p, H, hashlen );//哈希值在这里

RFC中举例了各个常用算法组织成的 T：

MD2:     (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 02 05 00 04 10 || H.

MD5:     (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 05 05 00 04 10 || H.

SHA-1:   (0x)30 21 30 09 06 05 2b 0e 03 02 1a 05 00 04 14 || H.

SHA-224:  (0x)30 2d 30 0d 06 09 60 86 48 01 65 03 04 02 04  05 00 04 1c || H.

SHA-256: (0x)30 31 30 0d 06 09 60 86 48 01 65 03 04 02 01 05 00  04 20 || H.

SHA-384: (0x)30 41 30 0d 06 09 60 86 48 01 65 03 04 02 02 05 00 04 30 || H.

SHA-512: (0x)30 51 30 0d 06 09 60 86 48 01 65 03 04 02 03 05 00  04 40 || H.

SHA-512/224:  (0x)30 2d 30 0d 06 09 60 86 48 01 65 03 04 02 05  05 00 04 1c || H.

SHA-512/256:  (0x)30 31 30 0d 06 09 60 86 48 01 65 03 04 02 06  05 00 04 20 || H.

3：EM = 0x00 || 0x01 || PS || 0x00 || T

到此，EMSA-PKCS1-v1_5规范定义完毕，下一步才是真正的签名

4：计算C = EM^d mod n,得到C就是签名的最后结果。

（6）RSASSA-PSS签名流程

作用：RSA私钥签名

RSASSA-PSS 签名流程 使用了 EMSA-PSS 封装格式。

我们先描述 EMSA-PSS 封装格式，因为这是 RSASSA-PSS签名流程的一部分。

签名：若要对数据M进行签名 ，步骤：

1：计算 mHash = Hash(M)，其长度为hashlen

2：计算slen长度的随机值salt，这里slen取hashlen。

3：计算 M' = Hash(00 00 00 00 00 00 00 00 || mHash || salt)

4：计算 DB = PS || 0x01 || salt，PS是字节0。PS的长度是nLen - 2*hashlen - 2 。然后 到这里，待签名数据的内存布局如下

ptr = 00 00 00 ... 00 00 || 0x01 || salt || M' || 0xBC

       看上面这种内存布局，也就好理解为什么PS的长度是 nLen - 2*hashlen - 2 了。

5：进行MGF运算

5-1： 计算hash值mask

unsigned char counter[4] = {0};

mask = Hash(M' || counter);

counter++；

5-2：

ptr ^= mask;

ptr += hashlen;

5-3： 执行5-1，5-2，直到 ptr 中的 salt 也被 mask 异或运算 为止。最后的结果是 EM。

EM = maskDB || M' || 0xBC

换句话说，不考虑counter以及hash函数，maskDB, 是由M’亦或得到的。

6：执行 EM^d mod n 得到签名结果C。注意：RFC上，对EM的首字节还需要特殊处理，但是实际应用中，都是一个固定的操作，这里不说了。（具体见 9.1.1 节的 step 11 ）。

 

验签：

1：解密C，得到的结果是 EM。

2：解封装EM。EM解密出的结果是EM = maskDB || M' || 0xBC，验证签名没有EMSA-PKCS1-v1_5那么简单，因为EMSA-PKCS1-v1_5封装格式中没有随机值。所以这里需要进行文字描述。EMSA-PSS解封装的核心就是需要恢复salt，就是封装时的那个随机值。 如何恢复salt, 我们回顾签名第四步的ptr，salt就是M’前的hashlen字节的值，只是被mask亦或了。我们只需要再被mask亦或一次，就能恢复salt。那mask是什么，我们回顾签名第5-1步，mask = Hash(M' || counter);我们的EM 中是存在M’的，所以，验证签名的一方能够计算mask。换句话说，dataA ^ dataB = dataC，dataC ^ dataB = dataA，这个是简单的数学原理。既然我们有 dataC(EM), dataB(hash(M’+counter))，自然能得到 DataA。

3：执行MGF, 也就是签名流程的第5步，他的结果就是我们能够得到 签名流程第四步的ptr。即能够得到salt。

4：至此我们从EM得到salt，M’，然后我们的入参又有 M，接下来的步骤就是使用 salt 和 M 生成， M”，理论上 M” 和 M’ 是相等的。这就是验证的流程。

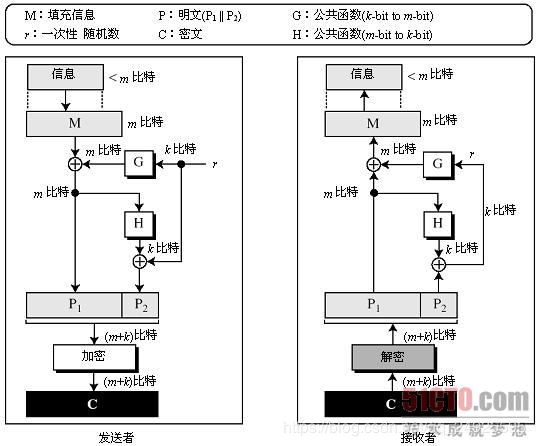
（7）RSAES-OAEP原理

         RSA中的一个短信息可以导致密文易遭受短信息攻击。也已经说明简单地给信息填充伪数据(填充位)也许就会使敌手的工作变得十分困难，但是通过更进一步的努力，她还可以对密文进行攻击。解决这种攻击的办法就是应用称为最优非对称加密填充(OAEP)的过程。下图，就是该过程的简单版本，执行时也许要用更为完善的版本。