核密度函数构建联合概率密度函数

核密度估计其实就是通过核函数（如高斯）将每个数据点的数据+带宽当作核函数的参数，得到N个核函数，再线性叠加就形成了核密度的估计函数，归一化后就是核密度概率密度函数了。

将设有N个样本点，对这N个点进行上面的拟合过后，将这N个概率密度函数进行叠加便得到了整个样本集的概率密度函数。

 

例如利用高斯核对X={x1=−2.1,x2=−1.3,x3=−0.4,x4=1.9,x5=5.1,x6=6.2}  六个点的“拟合”结果如下：
 

数据来源table2.csv

 

绘制二元分布

seaborn可以可视化两个变量的双变量分布。在seaborn中做最简单的方法是使用jointplot()函数，它创建一个多面板图，显示两个变量之间的双变量（或联合）关系以及每个变量的单变量（或边际）分布轴。

• 散点图

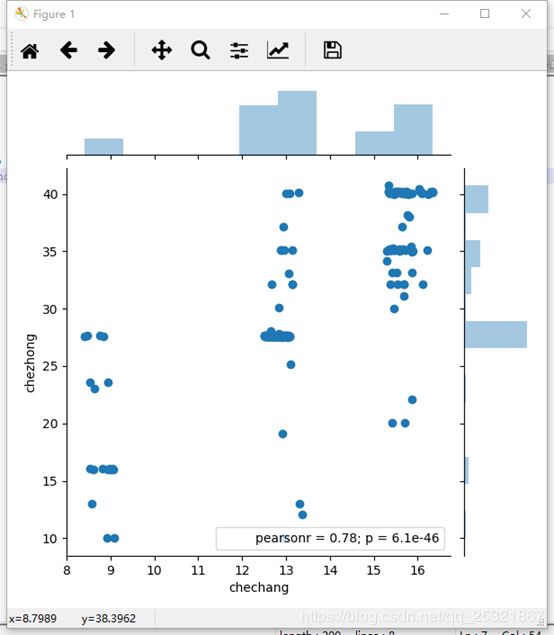
使二元分布可视化的最熟悉的方法是散点图，其中每个观测值以点和x和y值显示。这是在两个维度上的地毯图：

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

tips = pd.read_csv('table2.csv')
sns.jointplot("chechang", "chezhong", tips) 
plt.show()

• 核密度估计

也可以使用上述核密度估计过程来可视化双变量分布。在seaborn中，这种情节以等高线图显示，并且在jointplot()中作为样式提供：

import numpy as np

import seaborn as sns

import matplotlib.pyplot as plt

import pandas as pd

tips = pd.read_csv('table2.csv')

sns.jointplot("chechang", "chezhong", tips,kind='kde')

plt.show()

Pearson：皮尔森相关性系数  

r值表示在样本中变量间的相关系数，表示相关性的大小；

0.8-1.0 极强相关

0.6-0.8 强相关

0.4-0.6 中等程度相关

0.2-0.4 弱相关

0.0-0.2 极弱相关或无相关

p值是检验值，检验两变量在样本来自的总体中是否存在和样本一样的相关性，即显著水平

如果不显著,相关系数再高也没用,可能只是因为偶然因素引起的,

一般p值小于0.05就是显著了；如果小于0.01就更显著；