R软件做线性回归分析
做回归的一般步骤为:
1、确定回归方程中的解释变量和被解释变量
2、确定回归模型
通过观察散点图确定是建立线性回归模型还是非线性回归模型
3、建立回归模型
4、对回归方程进行各种检验
5、利用回归方程进行预测
下面就对线性回归模型的建立进行详细的阐述
一、获取数据
R软件里面有很内置的数据集,用data()函数可以查看到各种数据集
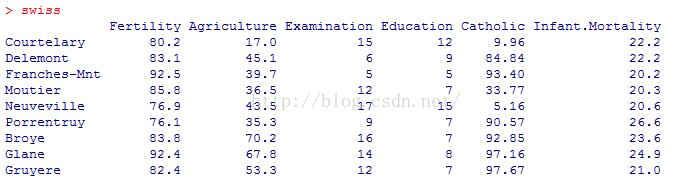
这里我们使用的是R软件自带的swiss数据集,这个数据集记录了瑞典1888年的生产力和其他各个社会经济指标的数据
首先对该数据集进行一个初步的了解
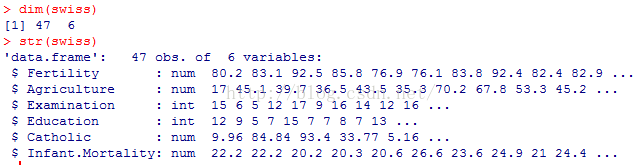
由运行结果可知该数据集有47行6列,每个变量都是数值型的
二、数据探索
1、数据质量分析
(1)缺失值分析:查看数据集中包含缺失值的记录数 sum(!complete.cases(swiss))
统计缺失值的个数 sum(is.na(swiss))
结果显示该数据集中没有缺失值,原因是因为该数据集是R自带的数据集,现实生活中我们的数据肯定是含有很多缺失值和异常值的,这时我们应该先对数据集有一个大致的了解,之后选择相应的处理办法。
(2)异常值分析:查看各个变量是否存在异常值,这里采用的是画箱型图的方式
box=boxplot(swiss)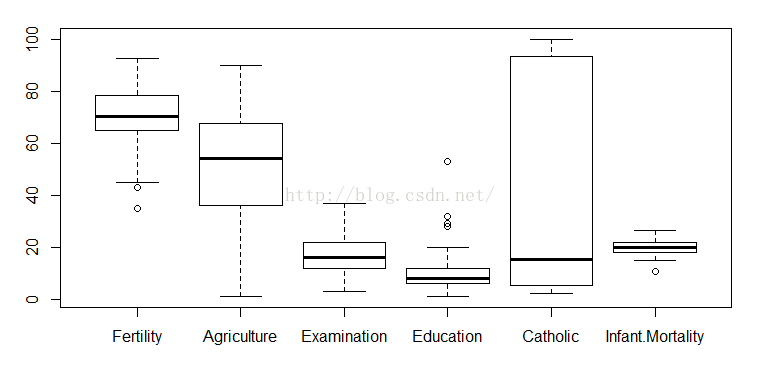
由上图可知,Fertility中包含2个异常值,Education中包含4个异常值,Infant.Mortality中包含1个异常值,结合实际情况,把这些值都归为正常值。
实际生活中,建模的数据中会包含很多的缺失值和异常值,在建模之前,我们首先应该对这些值进行处理之后才能开始建模。
2、各个变量之间的相关性分析:
(1)图形法:画散点图观察各个变量之间的关系
画散点图的函数有很多,这里使用的是car包里面的scatterplotMatrix函数,该函数相比plot()添加了很多功能
(各种散点图函数的介绍:http://www.statmethods.net/graphs/scatterplot.html)
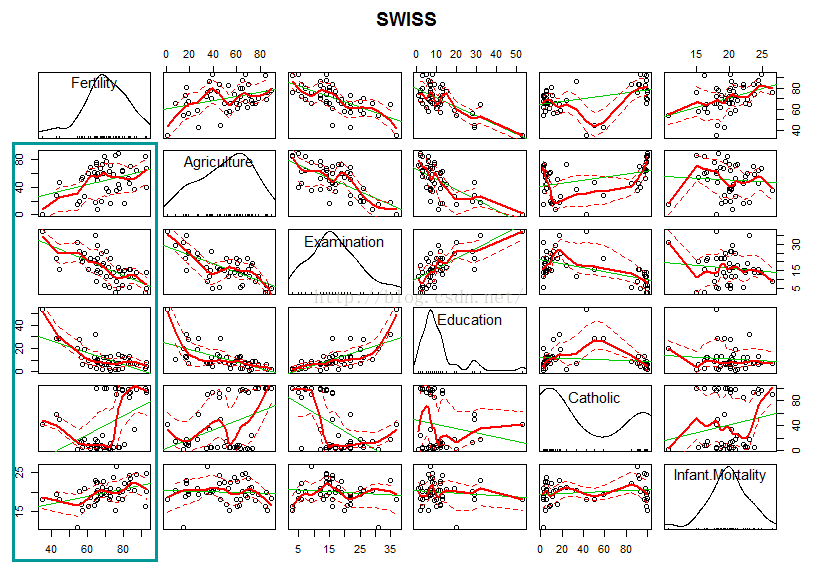
scatterplotMatrix(swiss,main="SWISS")
上图展示了各变量的密度图和各变量之间的散点图,有上图可知,Fertility和其他变量有相关性。
(2)计算相关系数: 这里用到的是psych包里面的 corr.test函数
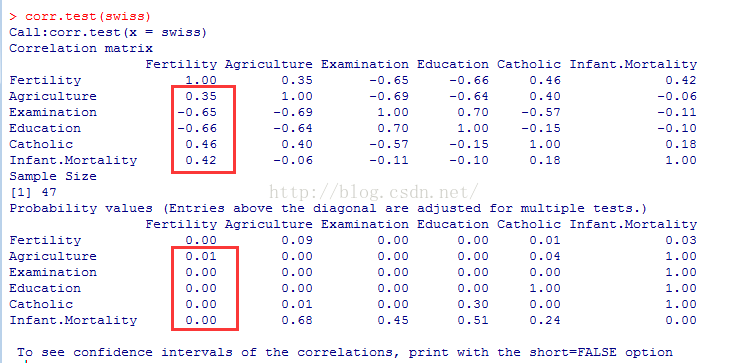
有上图可知,在0.05的显著性水平下,Fertility和其他变量的线性相关性能通过显著性检验。
三、建模
lmswiss=lm(Fertility~Agriculture+Examination+Education+Catholic+Infant.Mortality,data=swiss)
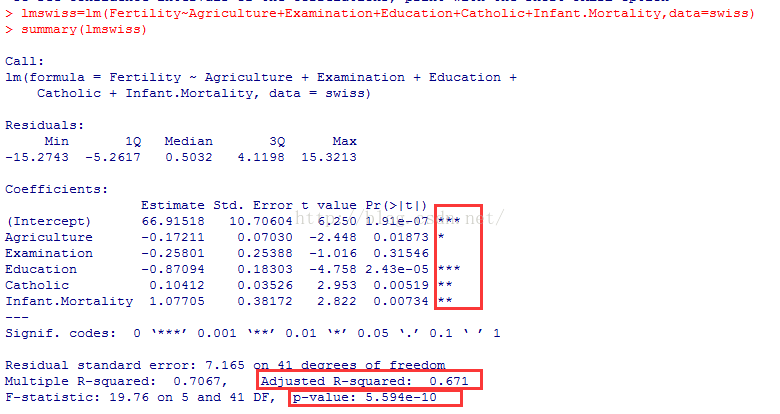
summary(lmswiss)
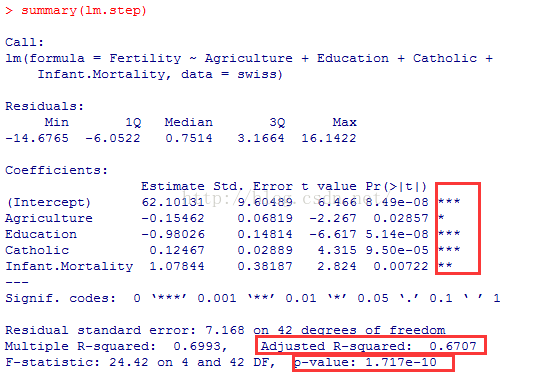
上图显示Examination的系数通不过显著性检验,
所以用逐步回归
lm.step=step(lmswiss)
summary(lm.step)
四、模型的检验
1.拟合优度检验:上图显示,调整的R平方为67%,说明生产力的波动有67%可以有这些自变量解释
2.显著性检验:F检验的p值接近于0,回归方程具有显著性
3.回归系数的显著性检验:在0.05的显著性水平下,各回归系数都能通过显著性检验
4.残差分析
获得回归方程的残差值:lm.res=resid(lm.step)
(1)正态性检验:回归方程的残差必须服从均值为0的正态分布
用shapiro.test函数检验残差是否服从正态分布,原假设为:服从正态分布
上图显示,我们不能拒绝残差服从正态分布的假设
(2)异方差检验:残差的方差不能随着Y值的变化而变化
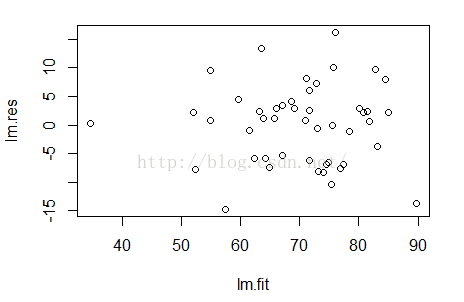
----画残差和拟合值的散点图
lm.res=resid(lm.step) #计算残差
lm.fit=predict(lm.step) #计算拟合值
散点图显示残差并没有随拟合值的变化而变化,而是随机的散落在X轴附近
----Breusch-Pagan 检验
----得分检验
2种检验的p值都大于0.05,说明残差不存在异方差
对于存在异方差的情况,我们可以使用WLS估计法(加权最小二乘法)、对数变换法等重新建立模型
(3)自相关检验
这里使用的函数是lmtest包里面的bgtest()函数
上图表明残差之间不存在自相关
在存在自相关的情况下,我们可以使用广义差分法消除自相关
5.变量之间无多重共线性
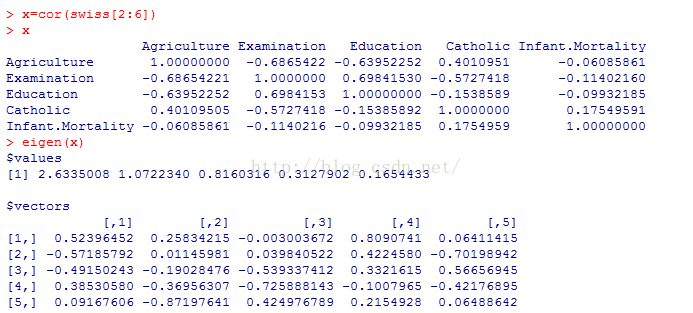
首先计算出自变量之间的相关系数:x=cor(swiss[2:6])
----求出变量相关系数x的特征值,如果某个特征值很小,或所有特征值的倒数之和为自变量数目的5倍以上,表明自变量间存在多重共线性
---用kappa函数检验多重共线性,如果值大于1000,说明变量之间存在严重的多重共线性
kappa值小于100,说明不存在多重共线性
逐步回归可以消除多重共线性的现象