Denoising Distantly Supervised Open-Domain Question Answering

摘要

远距离监督的开放领域问答（DS-QA）的目的是在未标记文本的集合中找到答案。现有的DS-QA模型通常从大型语料库中检索相关段落，并应用阅读理解技术从最相关的段落中提取答案。他们忽略了其他段落中包含的丰富信息。此外，远距离监督的数据不可避免地会伴随着错误的标签问题，而这些嘈杂的数据将大大降低DS-QA的性能。为了解决这些问题，我们提出了一种新颖的DS-QA模型，该模型采用段落选择器过滤掉那些嘈杂的段落，并使用段落阅读器从那些去噪的段落中提取正确答案。实际数据集上的实验结果表明，与所有baselines相比，我们的模型可以从嘈杂的数据中捕获有用的信息，并在DS-QA上取得重大改进。本文的源代码和数据可以从https://github.com/thunlp/OpenQA获得。

1.介绍

　　阅读理解旨在回答有关文档的问题，最近已成为NLP研究的重点。自从多层结构和注意力机制允许模型对问题进行推理，许多阅读理解系统被提出并取得了较好的结果。在某种程度上，阅读理解已显示出最新的神经模型具有阅读，处理和理解自然语言文本的能力。
　　尽管取得了成功，但现有的阅读理解系统仍依赖于预先确定的相关文本，而这些文本在现实世界中的问答系统中并不总是存在。因此，阅读理解技术不能直接应用于开放领域的QA任务。近年来，研究人员尝试使用大规模的未标记语料库来回答开放域问题。Chen et al. (2017) 提出了一种远距离监督的开放领域问答系统（DS-QA），该系统使用信息检索技术从Wikipedia中获取相关文本，然后应用阅读理解技术来提取答案。
　　尽管DS-QA提出了一种有效的策略来自动收集相关文本，但是它始终遭受噪声问题的困扰。例如，对于“Which country’s capital is Dublin?”这一问题，我们可能会遇到以下文本：（1）检索到的段落“Dublin is the largest city of Ireland …”实际上并未回答该问题；（2）检索到的段落“Dublin is the capital of Ireland. Besides, Dublin is one of the famous tourist cities in Ireland and …”中的第二个“Dublin”并非正确的答案。这些噪声段落和字符在DS-QA中被视为有效实例。为了解决这个问题，Choi et al. (2017)将DS-QA中的答案生成分为两个模块，包括选择文档中的目标段落和通过阅读理解从目标段落中提取正确答案。此外，Wang et al. (2018a)使用强化学习来共同训练目标段落选择和答案提取。
　　这些方法仅根据最相关的段落提取答案，这将丢失那些被忽略的段落中包含的大量丰富信息。实际上，正确的答案通常会在多个段落中提到，而问题的不同方面可能会在多个段落中得到回答。因此，Wang et al. (2018b)建议进一步明确汇总来自不同段落的证据，以对提取的答案进行重新排序。然而，重新排序方法仍然依赖于现有DS-QA系统获得的答案，并且不能充分解决DS-QA的噪声问题。
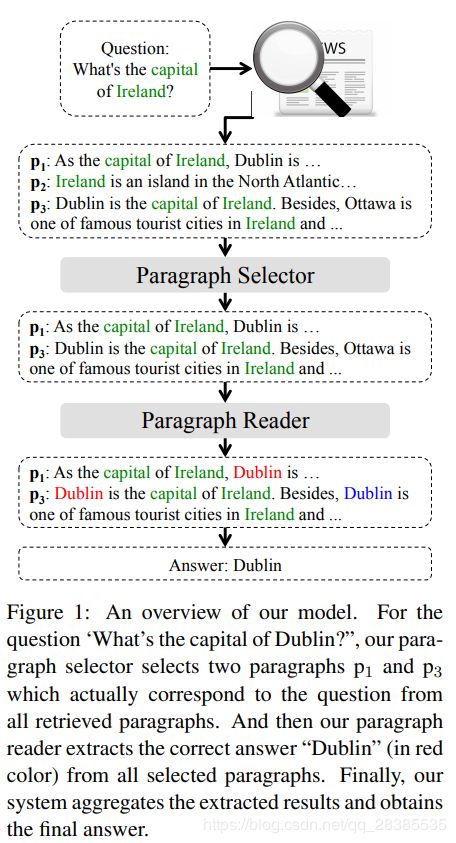
　　为了解决这些问题，我们为DS-QA提出了从粗到细的降噪模型。如图1所示，我们的系统首先通过信息检索从大型语料库中根据问题检索段落。之后，为了利用所有信息丰富的段落，我们采用了一个快速的段落选择器来浏览所有检索到的段落并过滤掉那些嘈杂的段落。然后，我们使用精确的段落阅读器对每个选定的段落进行仔细的阅读，以提取答案。最后，我们汇总所有选定段落的派生结果以获得最终答案。我们的方法中对段落选择器的快速浏览和对段落阅读器的密集阅读使DS-QA可以对嘈杂的段落进行降噪并保持效率。
　　在包括Quasar-T，SearchQA和TriviaQA的现实世界数据集上的实验结果表明，与所有baseline方法相比，我们的系统通过汇总所有内容丰富的段落的提取答案，实现了显着且一致的改进。特别是，我们表明，通过选择一些信息丰富的段落，我们的模型可以实现较好的性能，从而极大地加快了整个DS-QA系统的速度。我们将在Github上发布这项工作的所有源代码和数据集，以进行进一步的研究探索。

2.相关工作

问答是NLP中最重要的任务之一。在QA方面已经投入了很多努力，尤其是在开放领域的QA方面。开放领域QA最早是由(Green Jr et al., 1961)提出的。该任务旨在使用外部资源来回答开放领域的问题，例如文档集合，网页，结构化知识图谱或自动提取的关系三元组。
　　近年来，随着机器阅读理解技术的发展，研究人员试图通过对纯文本进行阅读理解来回答开放领域的问题。Chen et al. (2017) 提出了一种DS-QA系统，该系统从大型语料库中检索问题的相关文本，然后使用阅读理解模型从这些文本中提取答案。但是，在DS-QA中检索到的文本总是很嘈杂，这可能会损害DS-QA的性能。因此，Choi et al. (2017)和Wang et al. (2018a)尝试通过将问答分为段落选择和答案提取来解决DS-QA中的噪声问题，他们都只在所有检索到的段落中选择最相关的段落来提取答案，这丢失了那些被忽略的段落中包含的大量丰富信息。因此，Wang et al. (2018b)提出了基于强度和覆盖率的重新排名方法，该方法可以汇总现有DS-QA系统从每个段落中提取的结果，以更好地确定答案。但是，该方法依赖于现有DS-QA模型的预先提取的答案，并且由于仍然不加区别地考虑所有检索到的段落，因此仍然存在远程数据中的噪声问题。与这些方法不同，我们的模型采用段落选择器来过滤出那些嘈杂的段落并保留那些信息丰富的段落，从而可以充分利用嘈杂的DS-QA数据。
　　我们的工作还受到NLP中从粗到精模型的想法的启发。Cheng and Lapata (2016)和Choi et al. (2017) 提出了一种从粗到精的模型，该模型首先选择基本句子，然后分别对所选句子进行文本汇总或阅读理解。Lin et al. (2016)利用选择性注意聚合所有句子的信息以提取相关事实。Yang et al. (2016)提出了一个分层的注意力网络，在单词和句子层面上有两个层次的注意力用于文档分类。我们的模型还采用了从粗到精的模型来处理DS-QA中的噪声问题，该模型首先选择内容丰富的检索段落，然后从这些选定的段落中提取答案。

3.方法

在本节中，我们将详细介绍我们的模型。我们的模型旨在提取大规模未标记语料库中给定问题的答案。我们首先使用信息检索技术从开放领域语料库中检索与该问题相对应的段落，然后从这些检索的段落中提取答案。
　　 形式上，给定一个问题$q=(q^1,q^2,\cdot \cdot \cdot ,q^{|q|})$，我们将检索m个段落，定义为$P=\{p_1,p_2,\cdot \cdot \cdot ,p_m\}$的，其中$p_i=(p_i^1,p_i^2,\cdot \cdot \cdot ,p_i^{|p_i|})$是第$i$个检索到的段落。我们的模型测量在给定问题$q$和相应的段落集$P$的条件下提取出答案$a$的概率。如图1所示，我们的模型包含两个部分：
　　（1）段落选择器
　　给定问题$q$和检索到的段落$P$，段落选择器会测量所有检索到的段落的概率分布$Pr(p_i|q,P)$，该概率分布用于选择确实包含问题$q$答案的段落。
　　（2）段落阅读器
　　给定问题$q$和段落$p_i$，段落阅读器计算通过多层长短期记忆网络提取答案$a$的概率$Pr(a|q,p_i)$。
　　总体而言，给定问题$q$的条件下答案$a$被提取的概率$Pr(a|q,P)$可以计算为：
$$Pr(a|q,P)=\sum _{p_i\in P}Pr(a|q,p_i)Pr(p_i|q,P).\text{\hspace{1em}(1)}$$

3.1 段落选择器

由于DS-QA数据中不可避免地会出现错误的标注问题，因此在利用所有检索到的段落的信息时，我们需要过滤掉那些噪声段落。这很简单，我们只需要估计每个段落的置信度。因此，我们采用一个段落选择器来度量每个段落中包含答案的概率。
　　（1）段落编码
　　我们首先将段落$p_i$中的每个单词$p_i^j$表示为单词向量${p\text{p}p}_i^j$，然后将每个单词向量带入神经网络以获得隐藏的表示形式${\widehat{p\text{p}p}}_i^j$。在这里，我们采用两种类型的神经网络，包括：
　　1.多层感知器（MLP）
$${\widehat{p\text{p}p}}_i^j=MLP({p\text{p}p}_i^j),\text{\hspace{1em}(2)}$$
　　2.循环神经网络（RNN）
$$\{{\widehat{p\text{p}p}}_i^1,{\widehat{p\text{p}p}}_i^2,\cdot \cdot \cdot ,{\widehat{p\text{p}p}}_i^{|p_i|}\}=RNN(\{{p\text{p}p}_i^1,{p\text{p}p}_i^2,\cdot \cdot \cdot ,{p\text{p}p}_i^{|p_i|}\}),\text{\hspace{1em}(3)}$$
其中${\widehat{p\text{p}p}}_i^j$被编码为单词$p_i^j$及其周围单词的语义信息。对于RNN，我们选择一个单层双向长x短期记忆网络（LSTM）作为我们的RNN单元，并串联所有层的隐藏状态以获得${\widehat{p\text{p}p}}_i^j$。
　　（2）问题编码
　　与段落编码类似，我们还将问题中的每个单词$q_i$表示为其单词向量${q\text{q}q}_i$，然后将其带入MLP：
$${\widehat{q\text{q}q}}^j=MLP({q\text{q}q}^j),\text{\hspace{1em}(4)}$$
或者RNN：
$$\{{\widehat{q\text{q}q}}^1,{\widehat{q\text{q}q}}^2,\cdot \cdot \cdot ,{\widehat{q\text{q}q}}^{|q|}\}=RNN(\{{q\text{q}q}^1,{q\text{q}q}^2,\cdot \cdot \cdot ,{q\text{q}q}^{|q|}\}).\text{\hspace{1em}(5)}$$
其中${\widehat{q\text{q}q}}^j$是单词$q^j$的隐藏表示形式，表示为对其进行上下文信息的编码。之后，我们对隐藏的表示进行self-attention操作，以获得问题$q$的最终表示$q\text{q}q$：
$$\widehat{q\text{q}q}=\sum _j{\alpha }^j{\widehat{q\text{q}q}}^j,\text{\hspace{1em}(6)}$$
其中${\alpha }_j$编码每个疑问词的重要性，并计算为：
$${\alpha }_j=\frac{exp({w\text{w}w}_b{q\text{q}q}_i)}{{\sum }_{j}exp({w\text{w}w}_b{q\text{q}q}_j)},\text{\hspace{1em}(7)}$$
其中$w\text{w}w$是可学习的权重向量。
　　接下来，我们通过最大池化层和softmax层计算每个段落的概率：
$$Pr(p_i|q,P)=softmax(\underset{j}{\max }({\widehat{p\text{p}p}}_i^{j}W\text{W}Wq\text{q}q)),\text{\hspace{1em}(8)}$$
其中$W\text{W}W$是可学习的权重矩阵。

3.2 段落阅读器

段落阅读器旨在从段落$p_i$中提取答案。与段落选择器类似，我们首先通过多层双向LSTM将每个段落$p_i$编码为$\{{\overline{p\text{p}p}}_i^1,{\overline{p\text{p}p}}_i^2,\cdot \cdot \cdot ,{\overline{p\text{p}p}}_i^{|p_i|}\}$。并且我们还通过self-attention及多层双向LSTM获得了问题嵌入$\overline{q\text{q}q}$。
　　段落阅读器旨在提取最可能是正确答案的字符范围。然后将其划分为预测答案范围的开始和结束位置。因此，从给定的段落$p_i$中提取问题$q$的答案$a$的概率可以计算为：
$$Pr(a|q,p_i)=P_s(a_s)P_e(a_e),\text{\hspace{1em}(9)}$$
　　其中$a_s$和$a_e$表示段落中答案$a$的开始和结束位置，$P_s(a_s)$和$P_e(a_e)$分别是$a_s$和$a_e$作为开始词和结束词的概率，其计算公式为：
$$P_s(j)=softmax({\overline{p\text{p}p}}_i^j{W\text{W}W}_s\overline{q\text{q}q}),\text{\hspace{1em}(10)}$$
$$P_e(j)=softmax({\overline{p\text{p}p}}_i^j{W\text{W}W}_e\overline{q\text{q}q}),\text{\hspace{1em}(11)}$$
　　${W\text{W}W}_s$和${W\text{W}W}_e$是两个要学习的权重矩阵。在DS-QA中，由于我们没有人工标记答案的位置，因此我们可能有段落中的多个字符与正确答案匹配。令$\{(a_s^1,a_e^1),(a_s^2,a_e^2),\cdot \cdot \cdot ,(a_s^{|a|},a_e^{|a|})\}$为段落$p_i$中与答案$a$匹配的开始和结束字符的位置集合。等式（9）进一步定义了两种方法：
　　（1）Max。也就是说，我们假设该段落中只有一个字符表示正确答案。在这个方法中，通过最大化所有候选标记的概率来定义提取的答案$a$的概率：
$$Pr(a|q,p_i)=\underset{j}{\max }\underset{s}{\mathrm{Pr}}(a_s^j)\underset{e}{\mathrm{Pr}}(a_e^j)\text{\hspace{1em}(12)}$$
　　（2）Sum。在这个方法中，我们认为所有与正确答案匹配的字符都相等。我们将答案提取概率定义为：
$$Pr(a|q,p_i)=\sum _j\underset{s}{\mathrm{Pr}}(a_s^j)\underset{e}{\mathrm{Pr}}(a_e^j)\text{\hspace{1em}(13)}$$
　　我们的段落阅读器模型的灵感来自先前的机器阅读理解模型，即(Chen et al., 2016)中所述的Attentive Reader。实际上，其他阅读理解模型也可以很容易地用作我们的段落阅读器。由于篇幅所限，本文仅探讨Attentive Reader的有效性。

3.3 学习和预测

对于学习的目标，我们使用最大似然估计定义损失函数$L$：
$$L(\theta )=-\sum _{(\bar{a},q,P)\in T}logPr(a|q,P)-\alpha R(P),\text{\hspace{1em}(14)}$$
其中$\theta$表示模型的参数，$a$表示正确答案，$T$是整个训练集，$R(P)$是段落选择器上的正则化项，以避免其过拟合。在此，$R(P)$定义为$Pr(p_i|q,P)$与概率分布$\mathcal{X}$之间的KL散度，其中如果段落$p_i$包含正确答案，则${\mathcal{X}}_i=\frac{1}{c_P}$（$c_P$是包含正确答案的段落数）， 否则为0。具体地说，$R(P)$定义为：
$$R(P)=\sum _{p_i\in P}{\mathcal{X}}_{i}log\frac{{\mathcal{X}}_i}{Pr(p_i|q,P)}.\text{\hspace{1em}(15)}$$
为了解决优化问题，我们采用如(Kingma and Ba, 2015)中所述的Adamax最小化目标函数。
　　在测试过程中，我们提取概率最高的答案$\hat{a}$如下：
$$\begin{gathered} \hat{a}=\underset{a}{\mathrm{argmax}}Pr(a|q,P) \\ =\underset{a}{\mathrm{argmax}}\sum _{p_i\in P}Pr(a|q,p_i)Pr(p_i|q,P)\text{\hspace{1em}(16)} \end{gathered}$$
　　在这里，段落选择器可以看作是对所有段落的快速浏览，它确定了每个段落包含答案的概率分布。因此，我们可以简单地汇总那些具有较高概率的段落的预测结果，从而加速模型阅读。