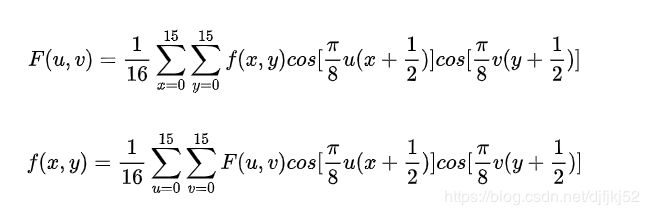2月21日 CVST工具箱模块仿真与图像处理（一）

课程地址：http://www.auto-mooc.com/chapter/study?class_id=C588FF7748E30CAB8B2C26AC901466C4&item_id=A26FBD880AF9AEB250A23688B1B471F4

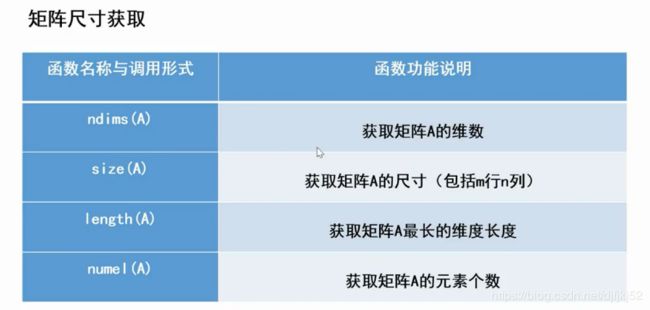
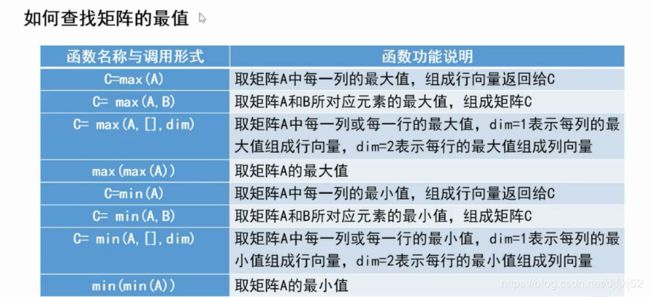
CVST工具箱

matlab

结构

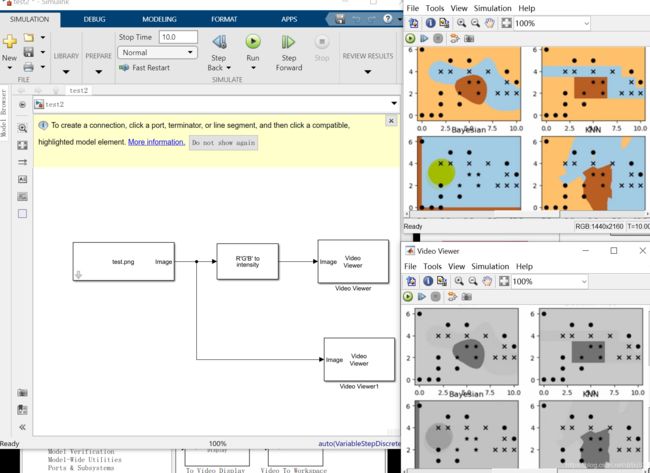
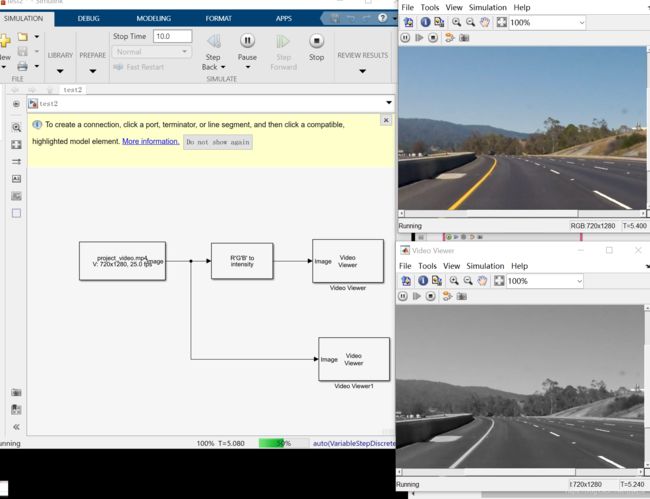
Simulink

CVST一个11类工具

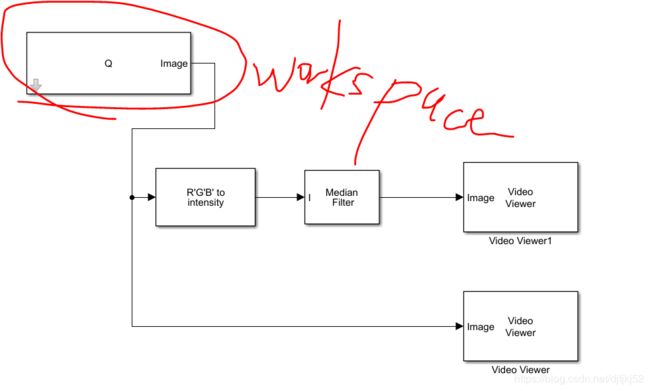
demo1：RGB的灰度仿真

图片灰度

视频灰度

导出代码

demo2 图像中值滤波

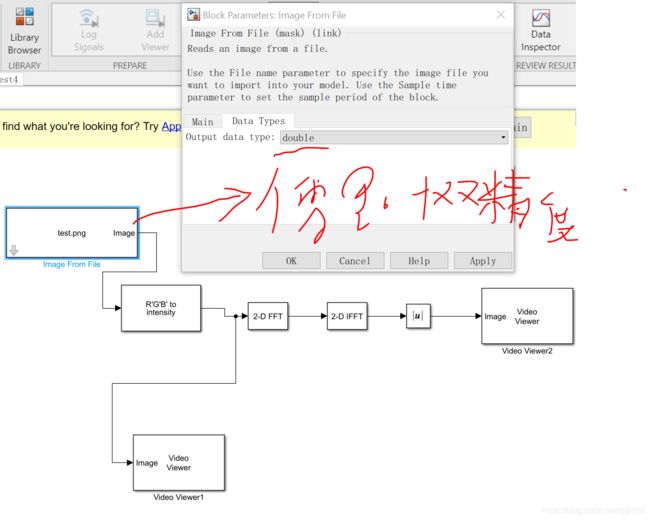
异常处理1：图像uint9——double的问题

现象：

I=double(imread("test.png"));
J=imnoise(I,"salt & pepper",0.02);

Q=imread("test.png");

P=im2double(imread("test.png"));
N=imnoise(P,"salt & pepper",0.02);

Matlab图像处理中uint8和double的问题
参考：https://blog.csdn.net/SMF0504/article/details/72899725

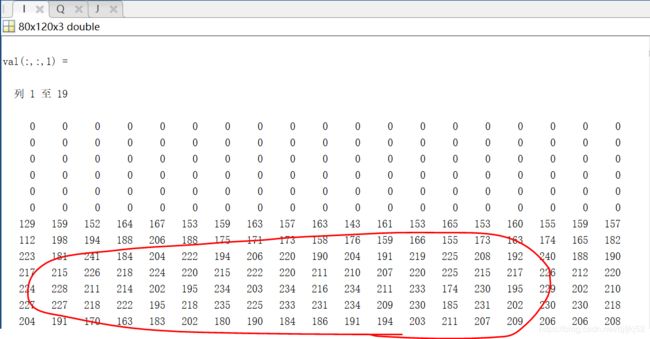
为了节省存储空间，matlab为图像提供了特殊的数据类型uint8(8位无符号整数），以此方式存储的图像称作8位图像。

imread把灰度图像存入一个8位矩阵，当为RGB图像时，就存入8位RGB矩阵中。

因此，matlab读入图像的数据是uint8，而matlab中数值一般采用double型（64位）存储和运算。所以要先将图像转为double格式的才能运算，

I2=im2double(I1)  %把图像I1转换成double精度类型 （假设图形矩阵范围0~255）
或者
I64=double(I8)/255;   %uint转换成double

如果不转换，计算会产生溢出。
意思也就是显示的时候用uint8 运算的时候用double；
即，主要是为了保持运算精度， 一般来说用double 来完成复杂的运算。而在存储的时候的一般存储为uint8类型，节省存储空间。

im2double():将图象数组转换成double精度类型
im2uint8():将图象数组转换成unit8类型
im2uint16():将图象数组转换成unit16类型

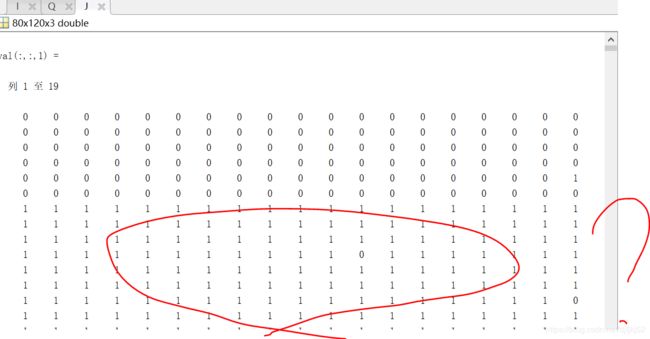
因为uint8的图像是灰度图像，也就是 像素值是从0~ 255变化的，而转换为double后像素值成了0~1变化，也就是说0是黑色，1是白色

使用”double（imread（”test.png“））会有错误

数字图像处理

学习主线

像素

灰度

典型图像变换的方法及仿真，如平移变换、图像的傅里叶变换等。

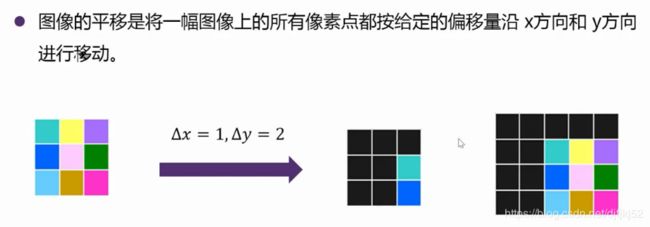
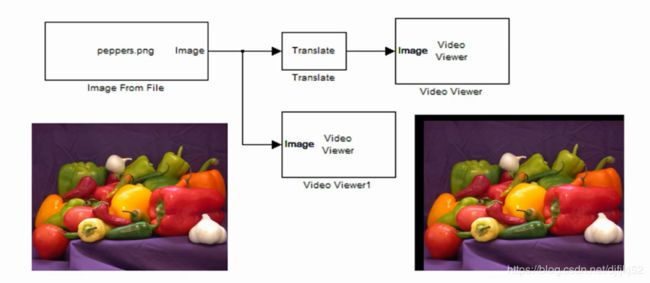
平移变换

demo：平移

时频域变换：傅里叶变换

demo：傅里叶变换

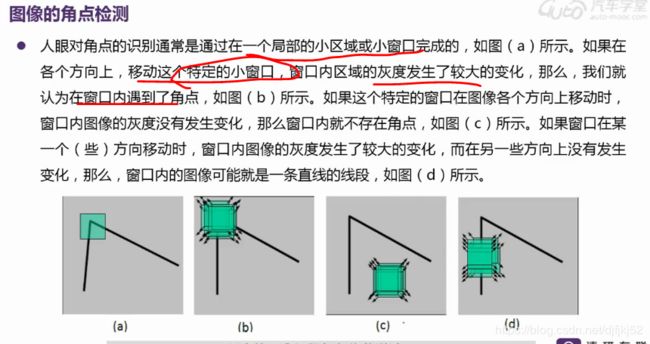
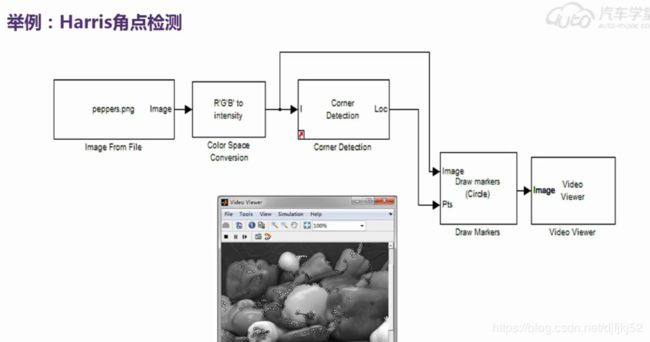
典型特征提取方法及模块儿化仿真，如Harris角点检测、图像边缘检测、尺度不变特征等。

demo 边缘检测

边缘可以分成两种

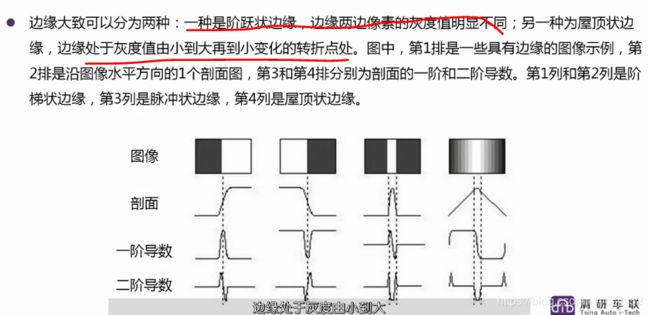
很多图像检测就是将图像矩阵求解一阶、二阶导数，根据导数变化以及变化的方向，例如sobel算子，prewitt算子，canny算子，基本原理相似

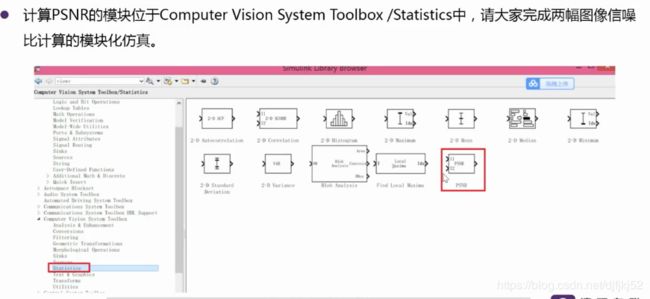
图像信噪比计算的模块化仿真

demo 信噪比

项目：离散余弦变换

离散余弦变换是与傅里叶变换相关的一种变换，类似于离散傅里叶变换，但是只使用实数。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换，这个离散傅里叶变换是对一个实偶函数进行的，在有些变形里面需要将输入或者输出的位置移动半个单位。—— 维基百科

傅里叶变换——傅里叶逆变换，对图像无影响

DCT变换，DCT又称离散余弦变换，是一种块变换方式，只使用余弦函数来表达信号，与傅里叶变换紧密相关。常用于图像数据的压缩，通过将图像分成大小相等（一般为8*8）的块，利用DCT对其进行变换，得到更加简洁的数据。因为图像像素间存在较大的空间相关性，DCT可以大大减小这些相关性，使图像能量集中在左上角区域，从而利于数据压缩。变换后得到的数据称为DCT系数。这一过程是无损的 。
————————————————
版权声明：本文为CSDN博主「彼岸之音」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/ahafg/article/details/48808443

1974年，K. R. Rao、N. Ahmed、T. Natarajan三位教授创立了离散余弦变换（Discrete Cosine Transform, DCT）。在数字信号、数字图像处理领域，离散余弦变换的效果能够接近理论上的最佳变换——Kahunen-Loeve变换（K-L变换）。

1807年，法国数学家、物理学家傅里叶（Jean Baptiste Joseph Fourier）提出了傅里叶变换（Fourier Transform, FT）。傅里叶变换的形式有很多种，归一化的二维离散傅里叶变换（Discrete Fourier transform, DFT）可以写成如下形式：

傅里叶变换包含复数运算，其运算复杂度和存储长度都超过实数运算。为了简化上述过程，同时达到更好的变换效果，余弦变换应运而生。

从傅里叶变换到离散余弦变换，需要一些数学理论的支持。在给定区间内满足狄利赫里条件的连续实对称函数，可以展开成仅含有余弦项的傅里叶级数。

对于定义在正实数域上的函数，可以通过偶延拓或奇延拓，满足上述条件。但如果函数的定义域包含零点 ，情况则稍有些复杂。

cite:https://zhuanlan.zhihu.com/p/33845296

DCT在算法层面的实现

为了简化离散余弦变换的计算过程，需要算法上进行优化。优化可以从两方面入手，一是降低计算次数，一是将浮点运算转化为整数运算。

为什么二维变换可以用矩阵表示

首先回顾一下什么样的图像可以使用 $T=AF{A}^T$来进行表示，要求二维变换核同时具备可分性与对称性且图像是正方形的图。当满足上述条件式，一个二维变换可以用两个一维变换计算，即首先变换图像的每一列再变换图像的每一行。对每一列进行变换就是用矩阵乘以图像的每一列，有线性代数知识可知
$XF=X[f_1,f_2,f_3,\dots ,f_n]$

其中的F是图像矩阵，而 $f_1,f_2,f_3,\dots ,f_n$ 是图像矩阵中的每一列。
————————————————
版权声明：本文为CSDN博主「独孤呆博」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/dugudaibo/article/details/78410570

DCT在硬件层面的实现

我们先不谈DSP等专用芯片，单说CPU与GPU。

计算机的运算可以分为两类，整数运算和浮点运算；浮点运算又可以分为两类，单精度浮点运算和双精度浮点运算。

GPU拥有大量并行流处理器，但缺少串行逻辑控制机构，擅长进行浮点预算，对于更注重溢出检查的整数运算，反而是GPU的弱项；CPU作为中央处理器，则是两种运算通吃。

进一步考虑浮点运算，单精度浮点运算的复杂度低于双精度浮点运算。市面上常见的游戏显卡和TaiTan X，均是注重单精度浮点运算，而限制了双精度浮点运算。开普勒架构的游戏显卡，双精度浮点运算能力是单精度浮点运算的1/24；同时代的CPU，这一比值大约是1/2。

一般而言，对于物理建模与模拟（比如流体力学模拟、量子化学计算）、3D建模（其实也是一种意义上的物理建模），需要双精度浮点运算；对于一般的图形渲染（包括游戏渲染、视频渲染）、机器学习，需要单精度浮点运算。所以游戏显卡削弱双精度浮点运算，TaiTan X一个劲提升单精度浮点运算，以及1080Ti被视为平民机器学习神器，都是有其道理的。

回到离散余弦变换。的确，GPU的并行运算速度超过CPU。经过优化的整数离散余弦变换算法利于并行计算，更是突出了GPU的并行优势，但GPU并不擅长整数运算。此外，在实际应用中，离散余弦变换过程伴随着串行逻辑，这也GPU不能胜任的。随着GPU计算的火热，如何让GPU完成离散余弦变换成了学界热点。但目前来看，让CPU扮演主要角色，把一部分运算交给GPU实现加速，应当是比较现实的考虑。

DCT在应用层面的实现

以视频编码为例。1984年，H.261编码标准开始研究。1990年，H.261编码标准由国际电信联盟（ITU-T）发布。1993年，MPEG-1编码标准由国际标准化组织/国际电子学委员会（ISO/IEC）发布。自此，H.26X系列与MPEG-X系列开始了各自的更新换代，当然期间也有合作交易，比如大家可能比较熟悉的MPEG-2与大家可能不熟悉的H.262，其实是一个东西，又比如MPEG-4，包括了（早期的）MPEG-4、MPEG-4/AVC（=H.264）、MPEG-4/HEVC（=H.265）三个标准。

诶，好像就差H.263与MPEG-3没有提。前者随着技术的进步退出了历史舞台，后者则被毙掉了…

从H.261开始，离散余弦变换就被应用于视频编码中。当技术发展到H.264与H.265，就具体的数学计算而言，H.261创立的分块编码被后续标准沿用，H.264在亮度平面上的基本分块为8x8像素块，于是离散余弦变换是这个样子（代入N=8）：

在整个编码过程中，离散余弦变换的作用如下：

首先，按照图像处理的一般流程，进行采样、整量，完成连续数据到离散数据的量化。根据前面提到的算法优化，量化过程整合了离散余弦变换的浮点运算。

接下来，进行整数离散余弦变换。做这一变换有什么用？一方面，从图像处理的整体流程而言，变换后便于后续处理；另一方面，从编码的角度而言，变换后使图像信息集中，在数学上体现为描述关键信息的系数变少，相应的，所需存储空间降低，达到降低视频体积的目的。

实现代码：

clear;
clc;
I = [12,23,53,16;42,16,68,45;34,62,73,26;72,15,34,28];  %数据块
A = zeros(4);   %变换矩阵A,也可以通过函数dctmtx(n)求得
for i = 0:3
    for j = 0:3
        if i == 0
            a = sqrt(1/4);
        else
            a = sqrt(2/4);
        end
        A(i+1,j+1) = a*cos((j+0.5)*pi*i/4)
    end
end
D = A*I*A';     %DCT变换
D1 = dct2(I);   %matlab DCT函数进行DCT变换
D2 = A'*D*A;    %DCT逆变换

由结果可以看出，D，D1方式得到的DCT系数相同，说明矩阵形式的DCT变换公式是正确的，D2的数据与原数据I相同，实现了数据恢复。

另外通过运行函数dctmtx(4)可以发现得到的变换矩阵与A完全相同。

Matlab 函数实现

matlab实现离散余弦变换有两种方法：

• 一种为函数dct2( ), 使用函数dct2，该函数用一个基于FFT的算法来提高当输入较大的方阵时的计算速度。
• 另一种为函数dctmtx( ), 使用由dctmtx函数返回的DCT变换矩阵，这种方法较适合于较小的输入方阵（例如8×8或16×16）。
  ————————————————
  版权声明：本文为CSDN博主「彼岸之音」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
  原文链接：https://blog.csdn.net/ahafg/article/details/48808443

1. 函数：dct2( )

实现图像的二维离散余弦变换。调用格式为：
B = dct2(A)
B = dct2(A,[M N])
B = dct2(A,M,N)
式中A表示要变换的图像，M和N是可选参数，表示填充后的图像矩阵大小，B表示变换后得到的图像矩阵。其逆变换函数为idct2( );
代码如下：

I = imread('1_1.jpg');%输入灰度图像
D = dct2(I);          %DCT变换
D1 = idct2(D);        %逆变换
subplot(1,2,1);imshow(I);
subplot(1,2,2);imshow(uint8(D1));

在这里可以通过函数colormap查看变换系数D。利用不同灰度值，可以发现D中主要数据都分布在左上角。

imshow(log(abs(D)),[]);
colormap(gray(8));colorbar;

2. 函数：dctmtx( )

D = dctmtx(N)
式中D是返回N×N的DCT变换矩阵，如果矩阵A是N×N方阵，则A的DCT变换可用D×A×D’来计算。这在有时比dct2计算快，特别是对于A很大的情况。上面有提到过。

对于图像的DCT变换，这里还需用到一个函数blkproc( ),其功能为对图像分块进行DCT变换。
blkproc( )定义如下：
B = blkproc(A,[M N],Fun) ，A为输入图像，MN为块大小，Fun为处理函数
常用的方式为：
B = blkproc(A,[8,8],’P1xP2’,T,T’); T为变换矩阵，P1和P2为参数，代表Tx*T’ 。

%%灰度处理
close all;
clear all;
Img=imread('t2.png');
[n m a]=size(Img);%判断图像的大小

GrayImage= rgb2gray(Img);%调用MATLAB函数实现灰度化

% Img_Gray=zeros(n,m);
% for x=1:n%通过双循环对图像进行灰度化处理
%     for y=1:m
%      %  Img_Gray(x,y)=max(Img(x,y,1),max(Img(x,y,2),Img(x,y,3)));  %第一种方法实现灰度化
%      %   Img_Gray(x,y)=(Img(x,y,1)+Img(x,y,2)+Img(x,y,3))/3;%第二种方法实现灰度化
%         Img_Gray(x,y)=0.3*Img(x,y,1)+0.59*Img(x,y,2)+0.11*Img(x,y,3);%第三种方法实现灰度化
%     end
% end

%figure,imshow(Img);title('原图像')
%figure,imshow(GrayImage);title('调用系统函数实现灰度化')
%figure,imshow(uint8(Img_Gray));title('第三种方法')
%%图像double-float
I =  im2double(GrayImage);
D = dctmtx(8);
C = blkproc(I,[8,8],'P1*x*P2',D,D');  %D'为D的转置
mask1=[1 1 1 1 1 0 0 0
1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];
mask2=[1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];
mask3=[1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];

X = blkproc(C,[8,8],'P1.*x',mask1);  %保留15个系数
I1  = blkproc(X,[8,8],'P1*x*P2',D',D);    %重构图像
X2 = blkproc(C,[8,8],'P1.*x',mask2);  %保留10个系数
I2  = blkproc(X2,[8,8],'P1*x*P2',D',D);    %重构图像
X3 = blkproc(C,[8,8],'P1.*x',mask3);   %保留3个系数
I3  = blkproc(X3,[8,8],'P1*x*P2',D',D);    %重构图像
subplot(2,4,1);imshow(I);
subplot(2,4,2);imshow(I1);
subplot(2,4,3);imshow(I2);
subplot(2,4,4);imshow(I3);

上面代码中，通过求得图像DCT系数，利用mask等矩阵对其进行量化，保留左上角主要的系数值，对于右下角的值由于其为非常小的高频系数，量化去除后对于图像的质量影响不大，可以利用这一性质对图像进行压缩处理。可以看到系数保留越少，则图像质量越差。

保留系数越多则图像压缩质量越好，下面比较几幅图像质量，从左到右分别为原图，mask1，mask2，mask3；

基于系统对象的图像/视频处理编程

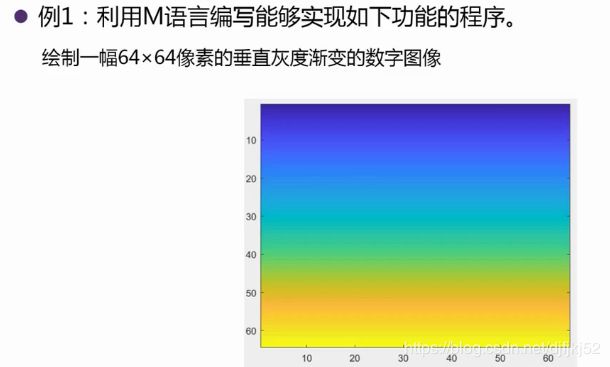
a=zeros(64,64);
for i=1:64
  for j=1:64
    a(i,j)=i;
end 
end
image(a)

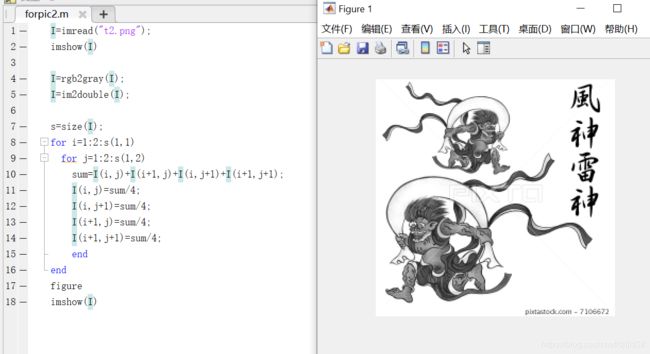
I=imread("t2.png");
imshow(I)

I=rbg2gray(I);
I=im2double(I);

s=size(I);
for i=1:2:s(1,1)
  for j=1:2:s(1,2)
    sum=I(i,j)+I(i+1,j)+I(i,j+1)+I(i+1,j+1);
    I(i,j)=sum/4;
    I(i,j+1)=sum/4;
    I(i+1,j)=sum/4;
    I(i+1,j+1)=sum/4;
    end
end
figure
imshow(I)

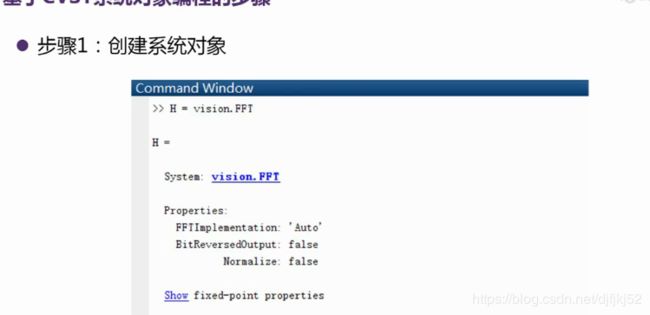
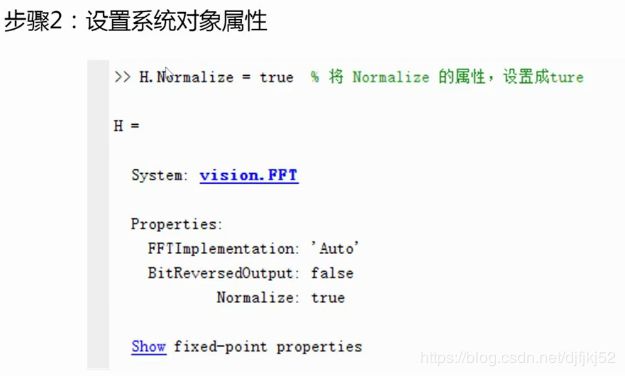
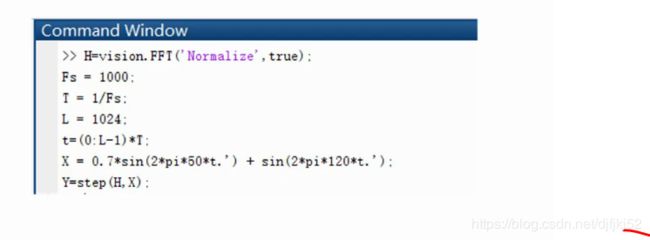
CVST系统对象编程

编程步骤

基于CVST系统对象编程的三个步骤，包括创建系统对象，设置系统对象属性，运行系统对象。

如下图，简化创建过程：

更加简化：

实例分析：

课程作业：

待续。。