基础数据结构——二叉树的遍历
1.二叉树的递归定义:
a.要么二叉树没有根节点, 是一棵空树。
b.要么二叉树由根节点、左子树、右子数组成,且左子树和右子树都是二叉树。
通俗的解释一波:
一个家族里面,可以把爷爷说成父亲的父亲,而曾祖父则为父亲的父亲的父亲,这样家族里自己的直系血缘的男性都可以用"父亲"这样的递归定义来定义了。
下面给出几种二叉树图:

D为完全二叉树, E为满二叉树。
2.完全二叉树与,满二叉树:
a.满二叉树:每一层的结点个数都达到了当层能达到的最大结点数。图中E为满二叉树,也就是说除了叶子结点,每一个结点都存在左孩子和右孩子。
B.完全二叉树:除了最下面一层,其余的每一层的结点个数都达到了当层能达到的最大结点数,且最下面一层只从左到右连续存在若干个点,而这些连续的结点全部不存在,上图的D、E都为完全二叉树。
满二叉树的结点存在一个公式,知道树的层数k可以推出存在2^(k - 1)个结点。
并且对于一个完全二叉树而言,除了根节点以外,任何一个结点的编号为x,每一个左孩子结点的编号为2x,右结点的编号为2 * x + 1.
##3.二叉树的存储结构:
a.一般来说,二叉树使用链表来定义,和普通链表的区别是,由于二叉树每个结点有两条出边,因此指针域变成两个——分别指向左子树的根节点与右子数的根节点,因此称为二叉链表。
struct node {
int data;
node* lchild;
node* rchild;
};
由于二叉树建树之前根节点不存在,因此地址一般为NULL。
node* root = NULL;
b.二叉树建立新的结点:
//二叉树新建结点
node* newNode(int v) {
node* Node = new node; //申请一个node型变量
Node -> data = v; //结点权值为v
Node -> lchild = NULL; //初始状态下没有左子树
Node -> rchild = NULL; //初始状态下没有右子数
return Node;
}
c.二叉树结点的查找、修改
查找操作是在给定数据域的条件下,在二叉树中找到所有数据域为给定的数据域的结点,并将它们的数据域修改为给定的数据域。
这里我们需要递归遍历二叉树。
我们可以先判定当前结点是否是需要查找的结点;如果是,对其进行修改操作,如果不是则分别往该节点的左孩子和右孩子进行递归,直到当前结点为NULL(递归出口)
//二叉树查找、修改操作:
void search(node* root, int x, int newdata) {
if (root == NULL) {
return ; //空树,(递归边界)
}
if (root -> data == x) {
root -> data = newdata;
}
search(root -> lchild, x, newdata); //往左子树递归
search(root -> rchild, x, newdata); //往右子树递归
}
d.二叉树的插入:
由于二叉树的形态众多,这里只能给出伪代码框架,根据适合的条件即可使用。
//二叉树插入
void insert(node* &root, int x) {
if (root == NULL) { //空树
root = newNode(x); //空树,说明查找失败,在这里插入,即为递归出口
return ;
}
if (由于二叉树的性质,x应该插在左子树) {
insert(root -> lchild, x);
} else {
insert(root -> rchild, x);
}
}
发现这里使用了引用,因为插入操作会改变二叉树的整棵树的结构,所以需要动态用引用去维护二叉树。
4.二叉树的遍历:
二叉树的遍历大概分为四种:先序遍历,中序遍历,后序遍历,层次遍历:
先说前面三种遍历吧,都属于递归遍历,也就是dfs
而后一种层次遍历则是bfs遍历。
为什么叫做先序遍历、中序遍历、后序遍历呢?
这里的先、中、后代表的是遍历根节点的次序。
如图:
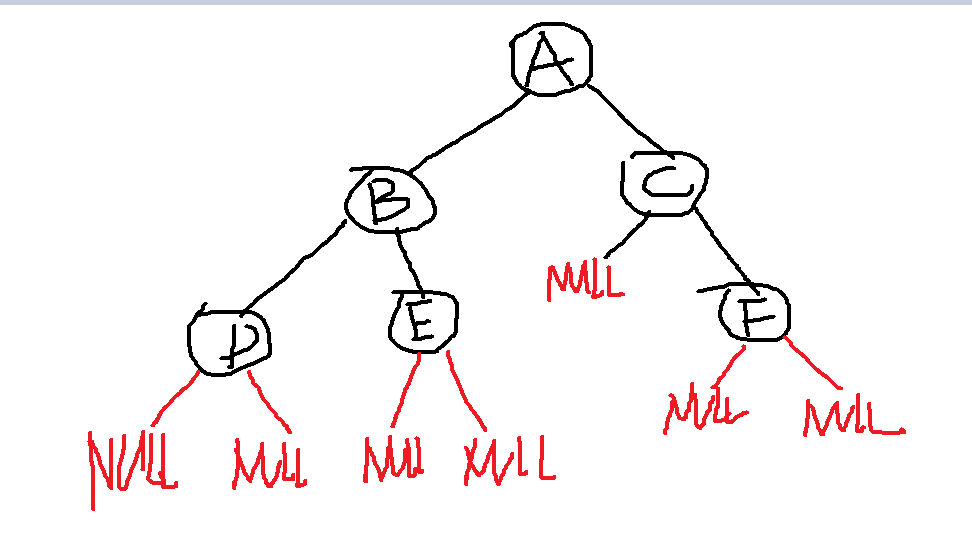
这样的一颗二叉树,
a.先序遍历:
如果是先序遍历则访问序列应该是根节点->左孩子->右孩子
所以先序遍历应该是
先从根节点A->访问左子树的根节点B->访问左子树根节点下的左子树D->访问左子树根节点下的右子树E->左子树已经访问完了,回溯到根节点A,访问右子树的根节点C->访问右子树下的右子树结点F(因为没有左子树了)。
即A->B->D->E->C->F
//二叉树先序遍历:
void preorder(node* root) {
if (root == NULL) return;
printf("%d->", root -> data);
preorder(root -> lchild); //访问左子树
preorder(root -> rchild); //访问右子树
}
b.中序遍历:
中序遍历的访问次序:左孩子->根节点->右孩子结点
首先访问左孩子结点发现A的左孩子为B,B的左孩子为D,D没有左孩子,所以先从D开始访问->然后返回根节点B->比那里右孩子结点E(发现没有做孩子节点或者右孩子结点返回根节点A) -> 找右子树的左孩子结点(发现为NULL)即找到右子树的根节点C遍历->继续遍历右子树的有孩子节点F.
遍历顺序应为:D -> B -> E -> A -> C -> F
//二叉树的中序遍历
void inorder(node* root) {
if (root == NULL) return;
inorder(root -> lchild);
printf("%d->", root ->data);
inorder(root -> rchild);
}
c.后序遍历:
后序遍历的访问次序:左孩子结点->右孩子结点->根节点
首先访问左孩子结点发现A的左孩子为B,B的左孩子为D,D没有左孩子,所以先从D开始访问->然后找到左子树的右孩子节点访问E->然后遍历左子树根节点B->然后访问根节点的右子树结点的右孩子点F->因为F没有子节点,访问右子树根节点C->最后范文整个二叉树的根结点A。
遍历次序:D->E->B->F->C->A
//二叉树后序遍历
void postorder(node* root) {
if (root == NULL) return ;
postorder(root -> lchild);
postorder(root -> rchild);
printf("%d->", root -> data);
}
d.层次遍历:
所谓层次遍历,就是一层一层的去访问。
如上图的二叉树:访问顺序:先访问第一层的根节点A->访问第二层的左子树结点B->访问第二层的右子树结点C->访问左子树的左孩子结点D->访问左子树的右孩子结点E->访问右子树的右孩子结点F
故为:A->B->C->D->E->F
层次比遍历从左向右遍历完每一层后在向下遍历,这就很像我们学习的广度优先搜索bfs的操作了,也要用到队列来实行操作。
//二叉树的层次遍历:
void LayerOrder(node* root) {
queue<node*> q; //这里存放的是结点地址,所以存放指针
q.push(root);
while (!q.empty()) {
node *now = q.front();
q.pop();
printf("%d->", now -> data);
if (now -> lchild != NULL) q.push(now -> lchild);
if (now -> rchild != NULL) q.push(now -> rchild);
}
}
5.已知二叉树的先序遍历序列(或者后序遍历序列)和中序遍历序列还原整棵二叉树:
a.已知二叉树的先序遍历序列和中序遍历序列:
假设我们所知先序序列为pre1…pren,已知中序序列为in1…inn
然后我们可以知道先序遍历最先遍历的是二叉树的根节点为pre1,我们已知这个条件以后我们遍历中序序列,找到某一个ink = pre1,那么我们可以知道在k的左边将二叉树分为了左子树和右子树。
我们设numleft = k - 1,numleft为左子树的结点个数,那么 n - k 就是右子树的个数了
在先序遍历区间的左子树区间为[2, k],中序遍历区间为[1, k -1]
在先序遍历区间的右子树区间为[k + 1, n],中序遍历区间为[k + 1, n]
我们就可以一直进行递归了,可以发现递归出口应该是当先序序列的长度小于等于0时,当前二叉树就不存在了,这就是递归边界。
//已知二叉树的先序遍历序列(或者后序遍历序列)和中序遍历序列还原整棵二叉树:
node* create(int preL, preR, inL, inR) {
//当前先序序列的区间为[preL, preR], 当前中序序列的区间为[inL, inR]
if (preL > preR) return NULL; //递归出口
node *root = new node; //建立一个新的结点,用来保存当前二叉树的根节点
root -> data = pre[preL]; //整棵二叉树的根节点
int k;
for (k = inL; k <= inR; k++) {
if (in[k] == pre[preL]) {
break; //找到了k的位置
}
}
int numleft = k - inL; //左子树的结点
//递归寻找左子树
root -> lchild = create(preL + 1, preL + numleft, inL, k - 1);
//递归寻找右子树
root -> rchild = create(preL + numleft + 1, preL, k + 1, inR);
return root;
}
b.已知后序序列和中序序列还原整棵二叉树:
其实和上面所说的一样,只不过后序遍历最后一个节点为根节点
假设后序序列为post1…postn, 中序序列为in1…inn
那么整棵二叉树的根节点就是post[n]
我们只要遍历中序序列找到根节点的位置在向上面一样划分左子树右子树的区间即可。
比如,
numright = k
后序左子树区间则为[1,k - 1] ,中序左子树区间[1, k - 1]
后序右子树区间则为[k, n - 1] ,中序右子树区间[k + 1, n]
//已知后序序列和中序序列还原整棵二叉树:
node* create(int postL, int postR, int inL, int inR) {
if (postL > postR) return NULL;
node* root = new node;
root -> data = post[postR];
int k;
for (k = postL; k <= postR; k++) {
if (post[postR] == in[k]) break;
}
int numleft = k - inL;
root -> lchild = create(postL, postL + numleft - 1, inL, k - 1);
root -> rchild = create(postL + numleft, postR - 1, k + 1, inR);
return root;
}
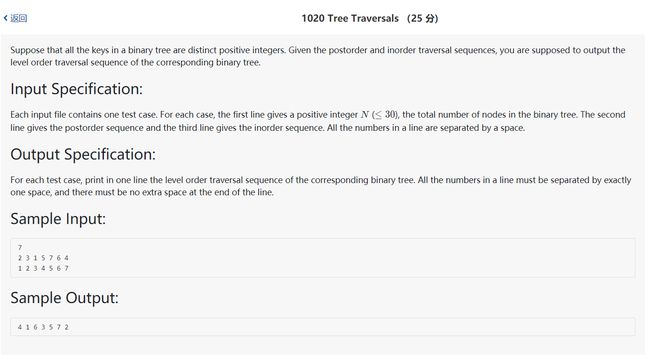
6.例题,PAT甲级1020Tree Traversals
b.分析:
这道题目就是说给出后序遍历序列和中序遍历序列要我们求出层次遍历序列,就是构建出原二叉树在进行bfs即可,看了上面的这里就很好写出代码了。
c.AC Code:
#include 欢迎关注ly’s Blog