电动摄像机-多输入多输出（MIMO）非线性自回归系统辨识（NARX）——基于MATLAB

目录

 

前言

1、输入输出的数据（测量数据序列）

2、非线性ARX（IDNLARX）模型-使用Wavenet（小波网络）的初步估计

3、非线性ARX模型-尝试更高阶

非线性ARX模型-调整非线性估计量的单位数

4、非线性ARX模型-尝试其他非线性估计器

5、具有混合非线性估计量的非线性ARX模型

---

前言

        本文出自 MATLAB2018A 的系统辨识 System Identification APP 中的 Example，因为自己在做这方面的课题，所以把这个例子简单做一下，包括翻译（Google 翻译，修改了部分问题）和自己的理解。

这个例子主要是用数据估计一种 MIMO 非线性黑盒系统的模型，工具箱提供了两种类型的非线性黑盒模型：NARX，Hammerstein-Wiener模型

1、输入输出的数据（测量数据序列）

        在此示例中将使用文件 'motorizedcamera.mat' 中保存的数据。 它包含从电动相机收集的188个数据样本，采样时间为0.02秒。 输入向量 u（t）由6个变量组成：固定在摄像机上的正交X-Y-Z坐标系中的3个平移速度分量[m / s]，以及绕X-Y-Z轴[rad / s]的3个旋转速度分量。 输出向量y（t）包含2个变量：点的位置（以像素为单位），该点是摄像机在3D空间中固定点拍摄的图像。 我们创建一个IDDATA对象 z 来保存加载的数据：

黑盒系统辨识最初始的东西就是数据。这个例子的数据来自于一个电动相机的数据，可以理解为控制6个输入量（6输入）的组合来达到要求的2个目标（2输出）。

load motorizedcamera          % 加载例子中的数据（内置）
z = iddata(y, u, 0.02, 'Name', 'Motorized Camera', 'TimeUnit', 's');  %创建一个iddata对象

来看一下运行情况：

可以知道，输入 u(t) 是一个188行，6列的矩阵，每一列代表一个输入变量的采样序列；同样的，y(t) 是188行，2列，每一列代表一个输出采样序列。以上就是我们所需要的数据，一般是从实验得到的。

2、非线性ARX（IDNLARX）模型-使用Wavenet（小波网络）的初步估计

        让我们首先尝试非线性ARX模型。 需要选择两个重要元素：模型阶数和非线性估计量。 首先尝试简单的事情，让我们选择顺序[na nb nk] = [ones（2,2），ones（2,6），ones（2,6）]。 这意味着每个输出变量都由所有输出和输入变量预测，每个变量都延迟了1个样本。 通过使用矢量符号，可以以 model_output（t）= F（y（t-1），u（t-1））的形式编写模型。 让我们选择小波网络（wavenet）作为非线性估计器，从而矢量非线性函数F将由两个小波网络估计。 MATLAB的函数 nlarx 有助于估计非线性ARX模型。

        小波的方法通常用于多分辨率的分析（详细请自行了解）。

mw1 = nlarx(z, [ones(2,2), ones(2,6), ones(2,6)], wavenet);

通过将模拟输出与估计模型的输出与测量数据z中的输出进行比较，检查结果：

compare(z,mw1)

结果：

结果就是使用小波网络时的非线性自回归的辨识效果，两个图分别表示两个输出的结果；每一幅图中的两条曲线分别表示原始系统的输出和采用了NARX辨识后的输出曲线。这里面并没有表现出与输入之间的关系，只是这种辨识的想过说明。这里面小波网络的方式只是 nlarx 函数的一个参数，它还有一些其他的参数方法，可以自行查询help。

3、非线性ARX模型-尝试更高阶

        让我们看看能否通过更高的阶次做得更好。 请注意，在使用基函数展开表示非线性来辨识模型时，模型参数的数量可能会超过数据样本的数量。 在这种情况下，某些估计指标（例如噪声方差和最终预测误差（FPE））无法可靠地计算。 对于当前示例，我们将关闭警告以告知我们有关此限制的信息。

ws = warning('off','Ident:estimation:NparGTNsamp');  % 关闭警告
mw2 = nlarx(z, [ones(2,2), 2*ones(2,6), ones(2,6)], wavenet);      % nb 参数乘2
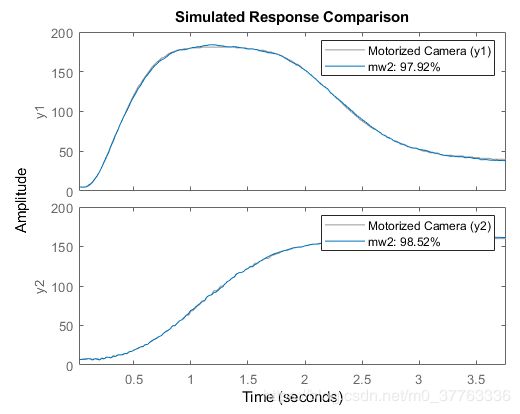
compare(z,mw2)

结果

第二个模型mw2很好。 因此，让我们在以下示例中保留对模型阶次的选择：

nanbnk = [ones(2,2), 2*ones(2,6), ones(2,6)];

估计算法已自动选择了两个小波网络估计器的单位数（子波）。 这些数字显示在下面。 注意缩写“ nl” =“Nonlinearity”和“ num” =“ NumberOfUnits”。

mw2.Nonlinearity(1).NumberOfUnits % 属性的全称Nonlinearity，NumberOfUnits
mw2.nl(2).num                     % MATLAB中可以使用的属性缩写 nl,num

非线性ARX模型-调整非线性估计量的单位数

       可以显式指定WAVENET估计器中的单位数，而不是由估计算法自动选择：

mw3 = nlarx(z, nanbnk, [wavenet('num',10); wavenet('num',5)]);  % 在选择方法时设置参数

4、非线性ARX模型-尝试其他非线性估计器

         在WAVENET估计器的位置，也可以使用其他非线性估计器。 让我们尝试TREEPARTITION估算器。

mt1 = nlarx(z, nanbnk, 'treepartition');

在上面的调用中，我们使用字符向量（“ treepartition”）代替对象来指定非线性估计量。 但是，这仅在将非线性与默认属性值一起使用时才有效。 在以下示例中，调用树分区对象构造函数以直接创建非线性估计器对象。

mt2 = nlarx(z, nanbnk, treepartition);

也可以使用SIGMOIDNET估计器。 可以使用NLARXOPTIONS命令指定诸如最大迭代（MaxIterations）和迭代显示之类的估计选项。

opt = nlarxOptions('Display','on');
opt.SearchOptions.MaxIterations = 2;
ms1 = nlarx(z, nanbnk, 'sigmoidnet', opt);

5、具有混合非线性估计量的非线性ARX模型

        在同一模型中的不同输出通道上可以使用不同的非线性估计器。 假设我们要使用树分区非线性估计器来预测第一输出，并使用小波网络来预测第二输出。 模型估计如下所示。 现在，第三个输入参数（非线性）是两个不同的非线性估计器对象的数组。

mtw = nlarx(z, nanbnk, [treepartition; wavenet]);

可以通过选择LINEAR估计器来指示输出通道中是否没有非线性。 以下示例表示，在model_output（t）= F（y（t-1），u（t-1），u（t-2））中，函数F由线性分量和非线性分量组成（ SIGMOIDNET）。

opt.Display = 'off'; % do not show estimation progress anymore
mls = nlarx(z, nanbnk, [linear; sigmoidnet('NumberOfUnits',5)], opt);
% no nonlinearity on first output

检查估计结果

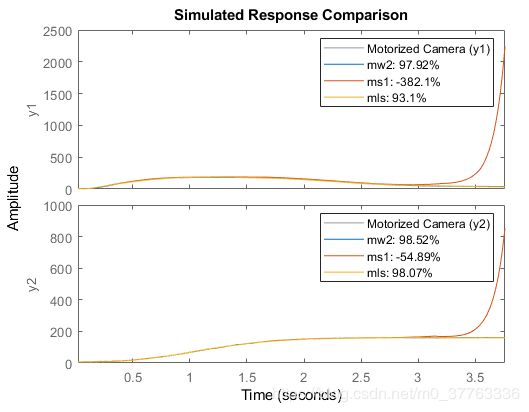
可以在同一COMPARE命令中比较各种模型。

compare(z, mw2, ms1, mls)

函数PLOT可用于查看各种模型的非线性响应。

plot(mt1,mtw,ms1,mls)

请注意，曲线图右侧的控制面板允许选择回归器和进行配置。

可以使用与线性模型相同的方法，在估计的模型上使用其他功能，例如RESID，PREDICT和PE。