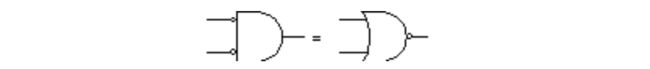编码的奥秘:逻辑门电路
转自:《编码的奥秘》 第十一章
在遥远的将来,当人们回顾2 0世纪的计算机发展史时,有人可能会以为一种称为“logic gates(逻辑门)”的设备是以著名的微软公司创始人的名字命名的( Bill Gates中的G a t e s在英语中有“门”的意思),其实并非如此。我们很快就会明白,逻辑门和通常让水和人通过的门十分相似。逻辑门通过阻挡或允许电流通过在逻辑中执行简单的任务。
回忆一下在上一章中你走进一个宠物店所要的那只猫,这可以由下面的布尔表达式说明:
同时,也可以用下面的电路来选择符合条件的小猫:
这样一个电路有时被称为网络。但在今天,网络这个词更多地被用来指连接起来的计算机,而不仅仅只是开关的集合。
尽管这个电路包含的全是1 9世纪发明的东西,但那时却没有人意识到布尔代数可以直接由电路实现。这种等同性直到2 0世纪3 0年代才被发现,主要贡献人是克劳德·香农(生于1 9 1 6年)。香农在他著名的、于1 9 3 8年在麻省理工学院所写的硕士论文《A Symbolic Analysis of Relay and Switching Circuits》中阐述了这个问题。(1 0年之后,香农的文章The Mathematical Theory of Communication》是使用“位( b i t )”这个字来表示二进制数字的第1篇出版物。)
1 9 3 8年以前,人们已经知道当把两个开关串联起来时,只有两个开关都闭合电流才能流通;而当把两个开关并联起来时,只需闭合其中的一个即可构成回路。但没有人能像香农那样清晰地阐述电子工程师可以使用布尔代数的所有工具来设计带开关的电路。此外,如果你简化了描述网络的布尔表达式,你也可以相应地简化网络。
例如,描述你想要的小猫的表达式是:
![]()
用结合律把用×结合的变量重新排序并按下面的方式重写表达式:
![]()
为更清楚地表达意图,可以定义名为X和Y的两个新变量:
现在,描述你想要的小猫的表达式可以写成下面的样子:
完成简化后,我们再把X、Y代回原来的式子。
注意,变量N在表达式中出现了两次。使用分配律,表达式可以按如下方式重写,并只使用一个N:
现在把X、Y表达式代入:
![]()
由于有很多圆括号,该表达式看上去似乎仍很复杂。但表达式中少了一个变量项(减少了一次×运算),也就意味着网络中少了一个开关。这是修改后的电路图:
确实,证明修改前后的两个电路图功能是一样的比去证明两个表达式功能是相同的要简单。
可是,网络中仍然多余了三个开关。理论上讲,你只需要四个开关来定义你心目中的猫咪。为什么是四个呢?因为每个开关都是一个“位”。你需要一个开关来定义性别(断开表示公的,而闭合表示母的);一个开关来定义是否有生育能力(闭合表示阄过的,断开表示未阄过的)还需要两个开关表示颜色。因为只有四种可能的颜色(白、黑、褐和其他所有颜色),而我们知道四种选择可以用两个二进制位来定义,所以只需要两个开关来表示颜色。例如,两个开关都断开表示白色,一个闭合表示黑色,另一个闭合表示褐色,两个开关都闭合就表示其他所有颜色。
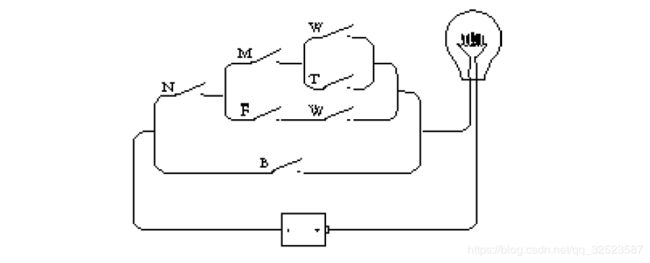
现在,让我们做一个控制面板来选择一只猫。控制面板上有四个开关(正如你家里的电灯开关)和一个灯泡:
开关打到上面是指开关闭合,反之是指开关断开。也许表示猫的颜色的两个开关标识得不是很清楚,这是为了把控制面板做得更简练不得已而造成的。在表示颜色的一对开关中,左边的开关标着B,如果只有它往上就表示黑色;右边的开关标着T,如果只有它往上就表示黄褐色;B、T两个开关均往上则表示其他颜色,由O标识;B、T两个开关均往下则表示白色,由W标识。
在计算机专业术语中,开关是一种输入设备,输入是控制电路如何工作的信息。本例中输入开关对应于描述一只猫咪的4位信息,输出设备是灯泡。如果开关描述了一只符合条件的猫,灯泡就会亮。上面介绍的控制面板上的开关被设置成表示一只无生育能力的黑母猫,这是符合你的要求的,所以灯泡亮了。
现在所要做的是设计一个使控制面板工作的电路。
前面提到过香农的论文题目是《 A Symbolic Analysis of Relay and Switching Circuits》,他所指的 r e l a y和第6章中所讲的电报系统的继电器很类似。在香农的论文发表时,继电器已被用作其他目的,尤其是用于电话系统的大型网络。
像开关一样,继电器也可以串联或并联以执行逻辑中的简单任务。继电器的组合称为逻辑门。这里所说的“逻辑门执行简单逻辑任务”是指逻辑门只完成最基本的功能。继电器比开关好是因为继电器可以被其他继电器控制而不必用手指控制,这意味着逻辑门可以被组合起来以执行更复杂的任务,比如一些简单的算术操作。事实上,下一章就要展示如何用电线连接开关、灯泡、电池和继电器来构造一个加法机(尽管它只能工作于二进制数字状态)。
继电器对电报系统的工作十分重要。连接电报站的电线长距离时电阻很大,需要一种方法来接收微弱的信号并把它增强后发送出去。继电器通过使用电磁铁控制开关可做到这一点。事实上,继电器放大了一个很弱的信号使其成为一个强信号。
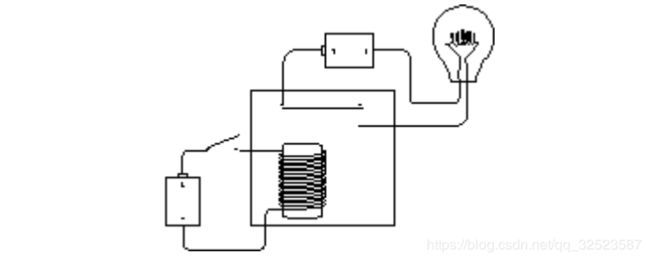
就我们的目的而言,我们并不对它的信号放大能力感兴趣,真正使我们着迷的是继电器作为开关可用电来控制而不用手指。可以用电线把继电器、开关、灯泡和一对电池做如下连接:
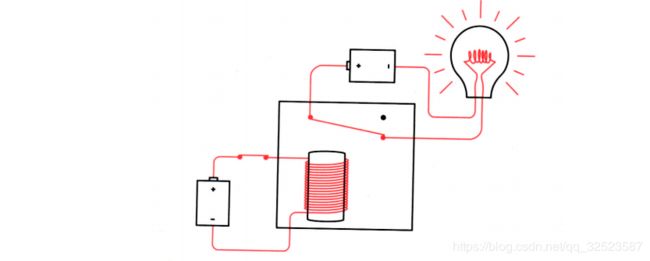
注意左边的开关是断开的,灯泡不亮。当闭合开关时,电流流过围绕在铁棒上的线圈,于是铁棒具有了磁性,并把上面有弹性的金属簧片拉下来,从而连通了电路,使灯泡发光:
当电磁铁把上面的金属簧片拉下来时,这个继电器被称为“触发了”。当左边的开关断开时,铁棒不再有磁性,继电器中的金属簧片则弹回到原来的位置。
这看上去似乎是用一种很不直接的方式点亮灯泡的,但实际上这种方式是很直接的。如果我们只对点亮灯泡感兴趣,我们完全可以舍弃继电器。但我们的兴趣并非只是点亮灯泡这么简单,我们有更宏伟的目标。
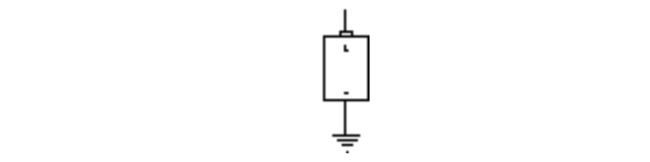
本章要多次用到继电器(当逻辑门建好之后就会很少再用了) ,所以要把上面那幅图简化一下。可以通过大地省去一些导线。在这种情况下,大地仅代表了一个公共端,并不是指真正的物理接地:
这看上去仍然不够简化,但还不至于那样做。注意两个电池的负极均接地,所以当看到的电池是这样的时:
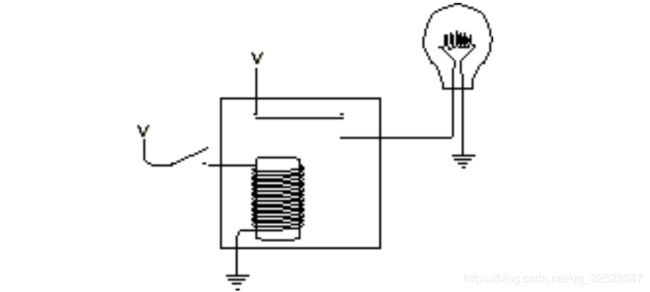
可用大写字母“ V(它代表电压) ”代替上图中的电池 (如在第 5和第 6章中所做的 )。现在继电器看上去如下图所示:
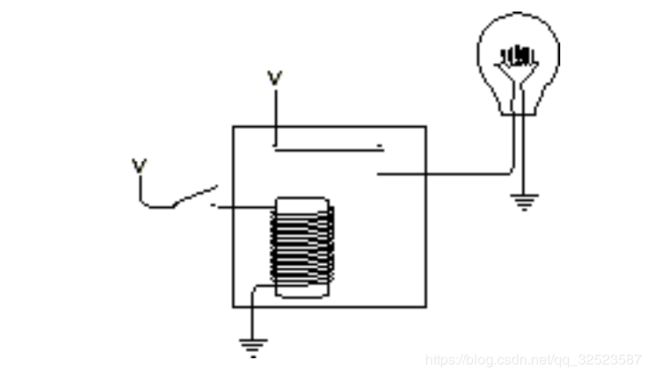
当右边开关闭合时,电流从 V端流出,经过电磁铁芯流到地上。这使得电磁铁把上面有弹性的金属簧片拉下来,从而连通了接有灯泡的电路,灯泡点亮: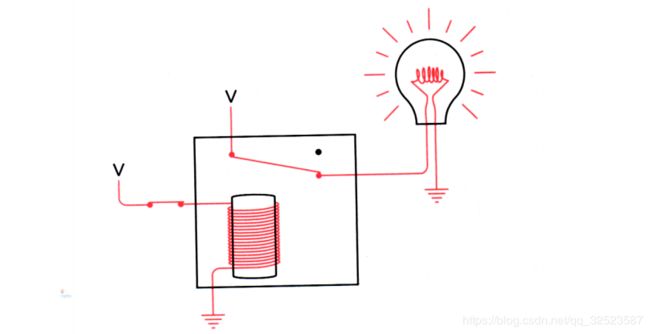
上面图显示了两个电源和两个接地,但本章的所有图中,电源,即“ V”,可以互连,接地端也可以互连。本章及下一章的所有继电器和逻辑门的网络只要求有一个电池,但可能是一个大容量的电池。例如,上一幅图可只用一个电池,如下所示:
但这幅图并不能清楚地表明要用继电器做什么。先不考虑电路而把注意力放到输入和输出上,就像前面的控制面板一样:
如果电流流经输入(例如,用一个开关把输入连到“ V”端) ,电磁铁就会被触发,输出就有了一个电压。
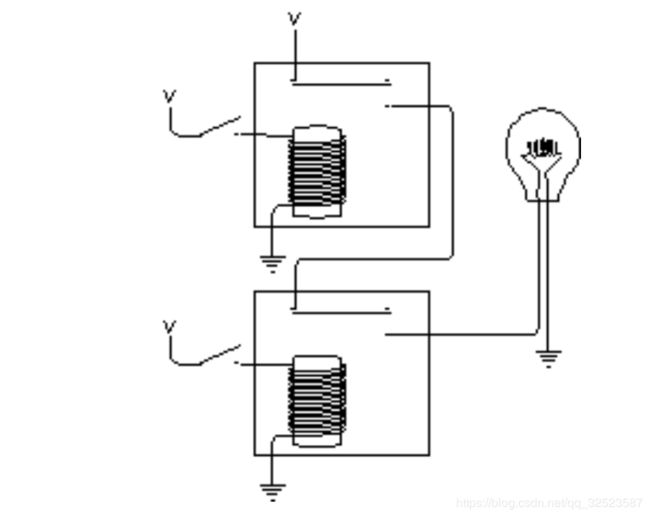
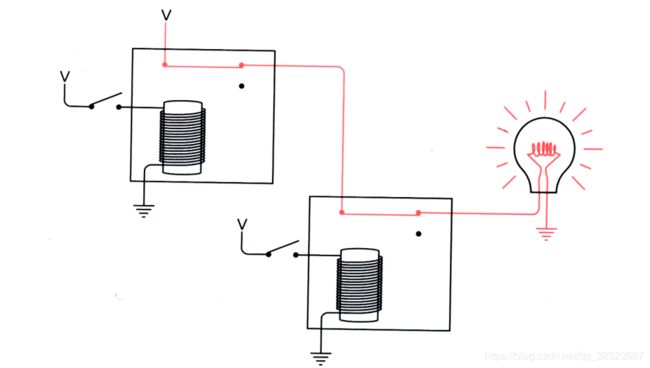
继电器的输入不一定只能是开关,其输出也未必只限于灯泡。一个继电器的输出可以连到另一个继电器的输入,如下所示:
当闭合开关时,第一个继电器被触发,它为第二个继电器提供了输入电压,于是第二个继电器也被触发,灯泡被点亮了:
把继电器连接起来是构造逻辑门的关键。
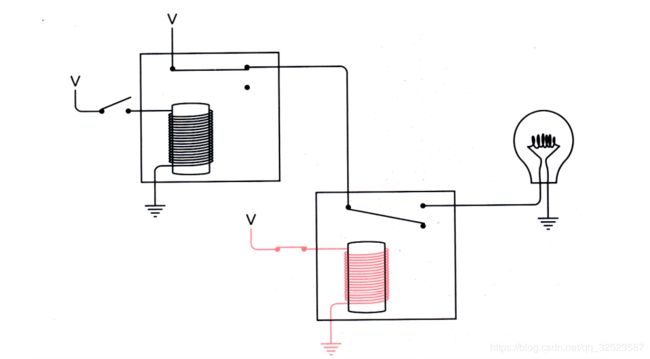
事实上,灯泡可以两种方式连到继电器上。注意,具有弹性的金属簧片是被电磁铁拉下来的。平时,金属簧片与上端接触,当电磁铁吸引它的时候,它便和下端接触。我们一直把金属簧片与下端的接触作为继电器的输出,但我们也可以把它与上端的接触作为输出。当使用这种输出时,结果正好相反,输入开关断开时灯泡是亮的:
而当输入开关闭合时,灯泡便灭了:
使用这种开关的继电器称为双掷继电器 ,它的两个输出在电性上是相反的—当一个有电压时,另一个则没有。
顺便说一下,如果你不知道现在的继电器是什么样子,你可以很方便地从当地的电器行的透明小包里看到一些。有些继电器就像 (加入饮料的 ) 方形小冰块一样大小,如元件号为2 7 5 - 2 0 6和 2 7 5 - 2 1 4的继电器就是这种大小的且经久耐用的继电器。它们被封在一个干净的塑料外壳里,所以你可以看到电磁铁和弹性金属簧片。本章和下一章所描述的电路都使用的是元件号为 2 7 5 - 2 4 0的继电器,它体积小且价格便宜(每个 $ 2.99)。
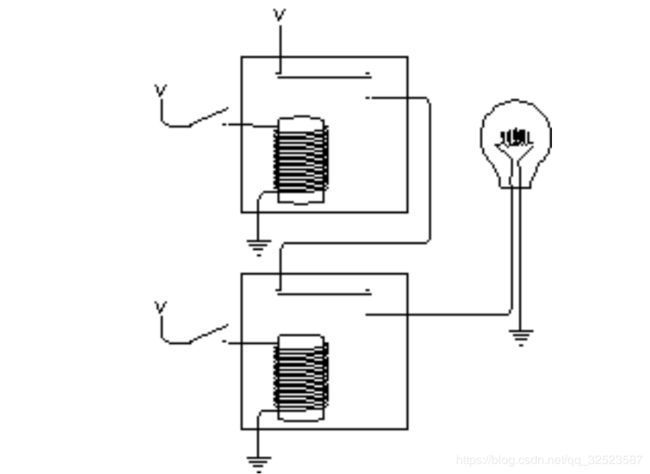
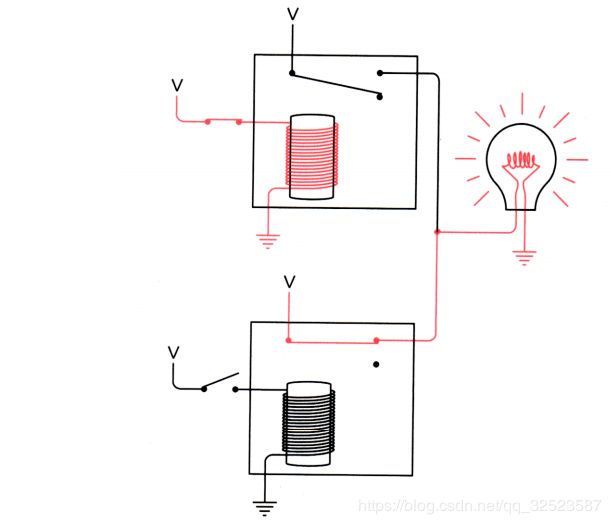
正如两个开关可被串联一样,两个继电器也可以串联:
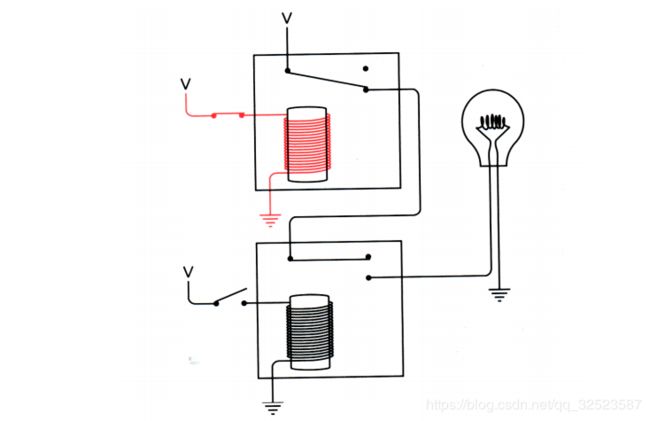
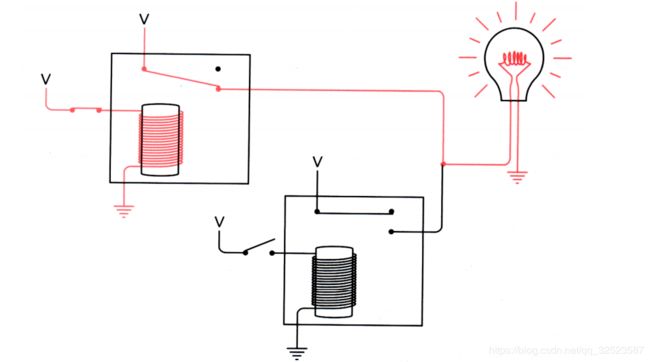
上面继电器的输出为下面的继电器提供了输入电压。如上所示,当两个开关均断开时,灯泡不会发光。试着闭合上面的开关:
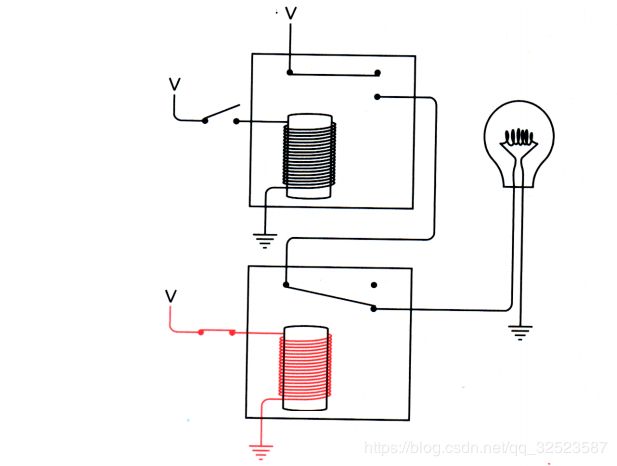
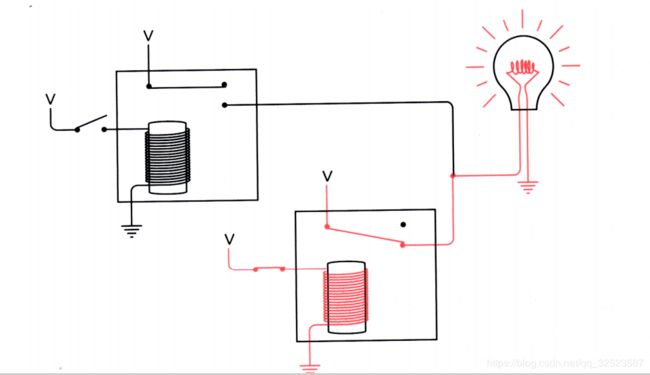
由于下面的开关仍旧断开,下面的继电器没有触发,所以灯泡仍然不亮。若断开上面的开关而闭合下面的开关:
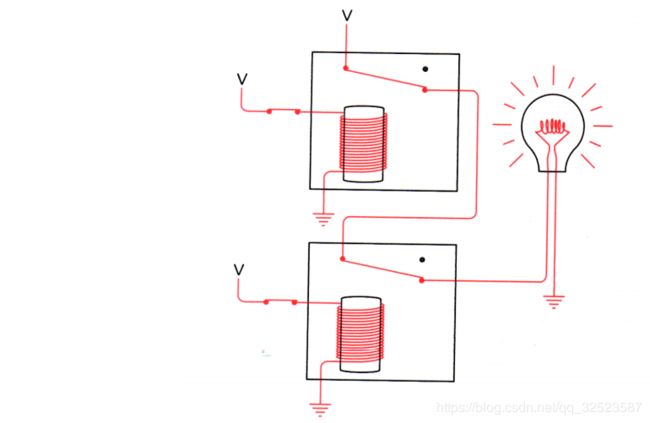
灯泡仍旧不亮。因为上面的继电器未被触发,电流无法流经灯泡。点亮灯泡的唯一方法是闭合两个开关:
现在,两个继电器都被触发了,电流可以在电源、灯泡和接地点之间流通。
同串联开关一样,这两个继电器也执行了逻辑操作。只有当两个继电器都被触发时,灯泡才会点亮。串联的两个继电器就是一个“ AND gate(与门)”。为避免复杂的图示,电气工程师使用一个特殊的符号表示“与门”,如下图示:
这是四个基本逻辑门中的第一个。与门有两个输入端(在图的左部) ,一个输出端(在图的右部) 。这样表示的与门通常输入在左部,输出在右部。这是因为人们习惯于从左到右读图。但是与门同样可以画成输入在上部、右部或底下。
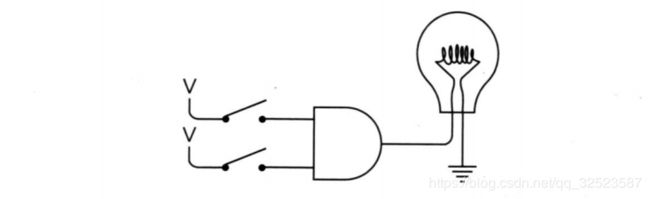
有两个继电器、两个开关和一个灯泡的原始电路图如下所示:
使用“与门”符号,上图可同样表示成:
注意与门不仅代替了串联的两个继电器,同时也隐含了上面的继电器连着电源,且两个继电器都是接地的。只有当上下两个开关都闭合时,灯泡才会发光,这就是它之所以叫与门的原因。
与门的输入未必一定要和开关连接,且输出也不一定只能是灯泡。我们真正要处理的是输入端的电压和输出端的电压。例如,一个与门的输出可以是另一个与门的输入:
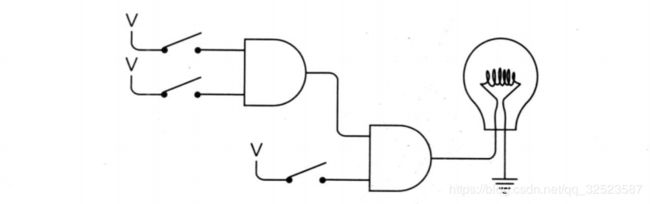
只有当三个开关都闭合时,灯泡才会发光。当上面的两个开关闭合时,第一个与门的输出会触发第二个与门的第一个继电器,而最下面的开关会触发第二个与门的第二个继电器。
如果把不加电压视为 0,加上电压视为 1 ,则与门的输出按如下方式由输入来决定:
正如两个串联的开关一样,与门的输入输出关系可作如下描述:
与门也可以有多于两个的输入端。例如,假设串联了三个继电器:
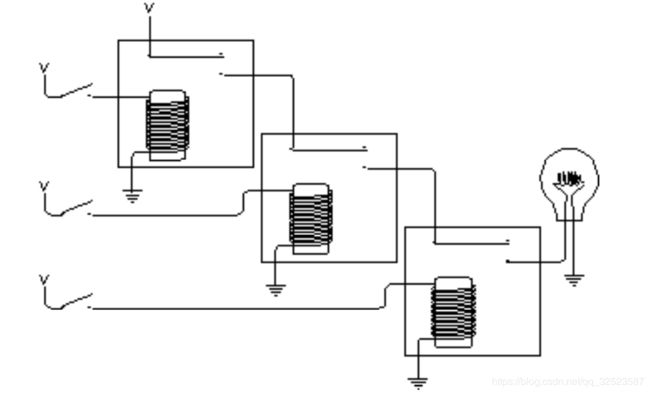
只有当三个开关同时闭合时,灯泡才会发光。这种配置可用如下符号表示:
它被称为三输入端与门。
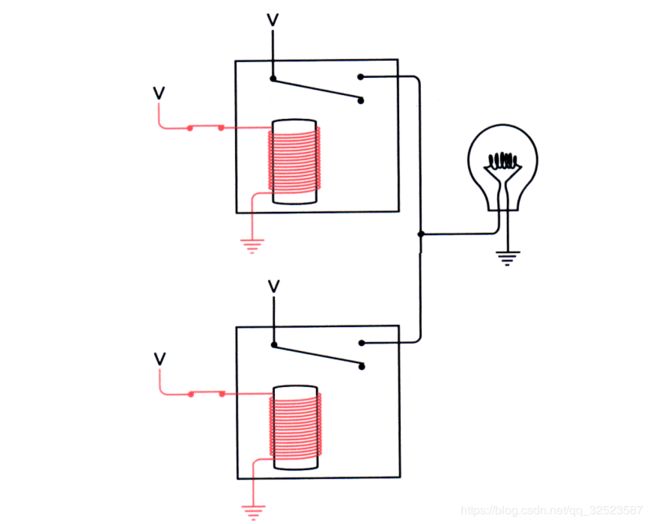
以下逻辑门可用并联的继电器解释:
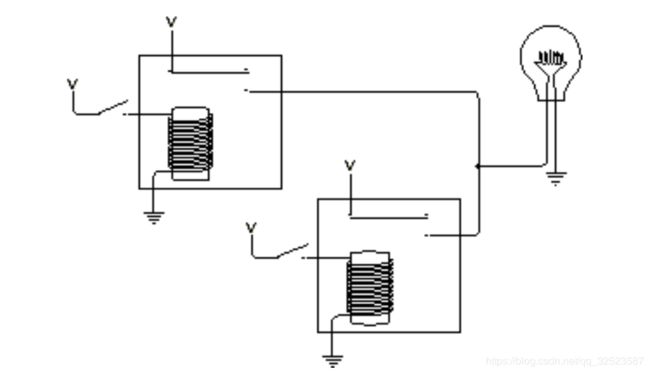
注意两个继电器的输出是连接在一起的,这个连接在一起的输出为灯泡提供了电源。任何一个继电器都可以点亮灯泡,例如,如果闭合上面的开关,灯泡会亮。这时,灯泡从左上角的继电器得到了电力供应。
如果让上面的开关断开而闭合下面的开关,灯泡也会亮:

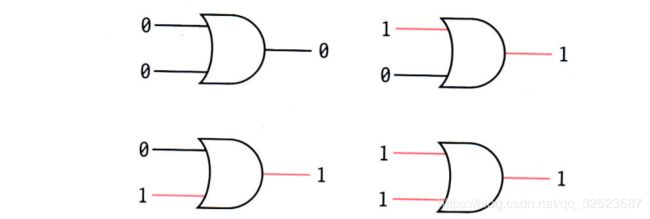
可见,当上开关或下开关中的任何一个闭合时,灯泡都会亮。这里的关键是“或”,所以这样的门叫“ OR gate(或门) ”。电气工程师使用如下符号表示或门:

它看上去和与门很相似,只是接输入端的一边是弧形的,很像英语“ O R”中的字母“ O”。
或门的两个输入中,只要有一个加上电压,输出就是高电位。同样,如果约定不加电压是0,而加电压是 1 ,则或门也有四种可能的组合状态:
可以把或门的输入输出关系小结成如下表格:
或门也可以有两个以上的输入端(当任一输入端为 1 时,输出端就为 1 ;只有所有输入端均为0时,输出端才为 0)。
前面解释过继电器可称为双掷继电器,因为其输出可以两种不同的方式连接。通常情况下,当开关断开时,灯泡不亮:
当开关闭合时,灯泡点亮。
也可以用另外一种连接方式,使开关断开时灯泡点亮:
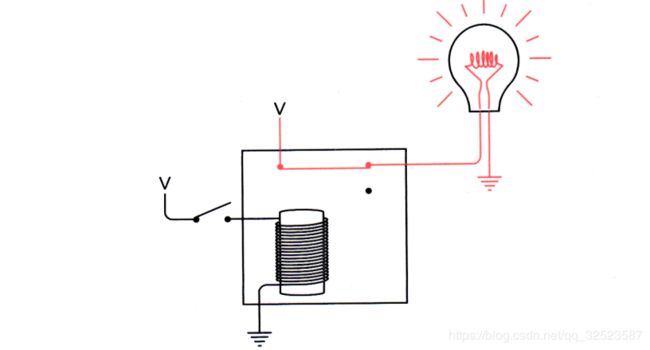
在这种情况下,只有闭合开关时灯泡才熄灭。以这种方式连接的继电器叫作 反向器 。反向器不是逻辑门(逻辑门通常有两个以上的输入),但它十分有用。反向器可以用下面的符号表示:

它被称为反向器的原因是当输入为 0时输出却为 1 ,反之亦然:
有了反向器、与门和或门,我们就可以制作控制板来自动选择理想的小猫了。让我们从开关开始。第一个开关的闭合表示母猫,断开表示公猫。这样,可以产生称为 F和 M的两个信号,如下图所示:

当F是1 , M就是0,反之亦然。同样,第二个开关的闭合表示阄过的猫,而断开表示有生育能力的猫:

接下来的两个开关更复杂一些,不同的组合要代表四种不同的颜色。这里有两个开关,都与电源相连:
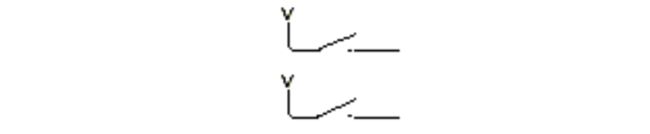
当两个开关都断开时,它们表示白色。我们用两个反向器和一个与门来产生信号 W。如果选择了一只白猫, W就为1 ,否则为 0:

当开关断开时,两个反向器的输入是 0,这样反向器的输出(也就是与门的输入)为 1 ,这也就意味着与门的输出为 1 。一旦一个开关闭合,与门输出即为 0。
为表示一只黑猫,闭合第一个开关,这可以用一个反向器和一个与门实现:
只有当第一个开关闭合而第二个开关断开时,与门的输出才是 1 。同样,当第二个开关闭合而第一个开关断开时,与门的输出也为 1 。我们用来表示褐色:

现在把四个小电路集成为一个大电路(通常,黑点表示电线的连接点,没有黑点的交叉线是不连接的):
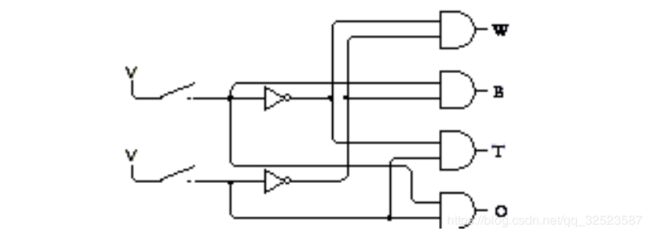
这个连接图看起来十分复杂。但如果仔细地沿着线路走,看清楚每个与门的输入而不要关心这些输入又连到了别的什么地方,你就会明白电路是如何工作的。如果两个开关都断开,信号W会是1 ,其余信号都是 0。如果第一个开关闭合,则信号 B会是1 ,其余信号都是 0。
连接门和反向器时可以遵循一些简单的规则:一个门(或反向器)的输出可以作为其他门(或反向器)的输入,但是两个以上的门(或反向器)的输出永远不能互连在一起。
由 4个与门和 2个反向器组成的电路叫作“ 2 - 4译码器”。输入是两个二进制位的不同组合,共代表了 4个不同的值。输出是 4个信号,任何时刻只能有一个是 1 ,至于哪一个是 1 取决于两个输入位。用同样的原理还可以构造“ 3 - 8译码器”或“ 4 - 1 6译码器”等等。
选择小猫的表达式的简化表示是:
对于表达式中的每一个加号 ( + ),必定对应电路中的一个或门。对于每一个乘号 (× ),则对应一个与门:
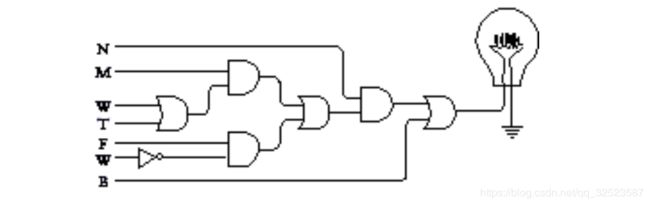
电路图左边的符号和它们在表达式中出现的顺序是一样的。这些信号来自于和反向器连接的开关及 2 - 4译码器的输出。注意,图中用了反向器来表示表达式中的( 1 -W)。
你可能会说: “这不过是一堆继电器而已。 ”不错,这正是一堆继电器,每个与门和或门中都有两个继电器,一个反向器中有一个继电器,因而只能说你必须习惯它。以后的各章会用更多的继电器。不过,所幸的是你不用真正地去买一堆回家连起来。
本章再看两个逻辑门。这两个门都会用到这样一个继电器,该继电器在不被触发时,其输出为高电位(这是用在反向器中的输出)。例如,下面配置中,一个继电器的输出为第二个继电器提供了电源。当两个输入都断开时,灯泡是点亮的:
如果上面的开关闭合了,灯泡就会熄灭:
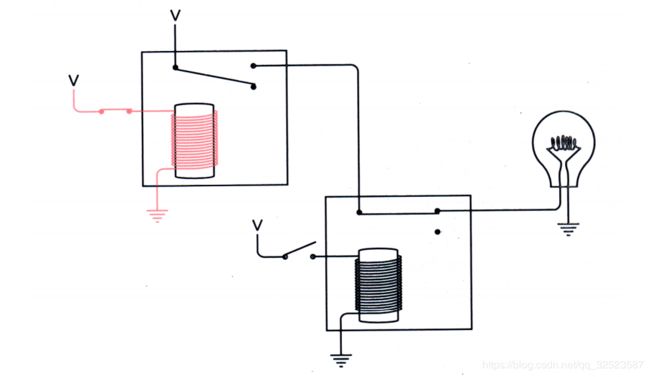
灯泡的熄灭是因为第二个继电器没有电源供应。同样,若下面的开关闭合灯泡也会熄灭:
若两个开关都闭合,灯泡还是不亮:
这种行为和或门的行为正好相反,被称为“ NOR gate (或非门) ”。下面是或非门的符号:

它和或门的符号很相像,只是在输出端有一个空心的小圆圈,这个小圆圈表示反向,故而或非门也可用下面的表示:

这张表显示的结果和或门相反。在或门中,输入端中只要有一个是 1 ,输出就是 1 ;只有输入端均为 0时,输出才为 0。
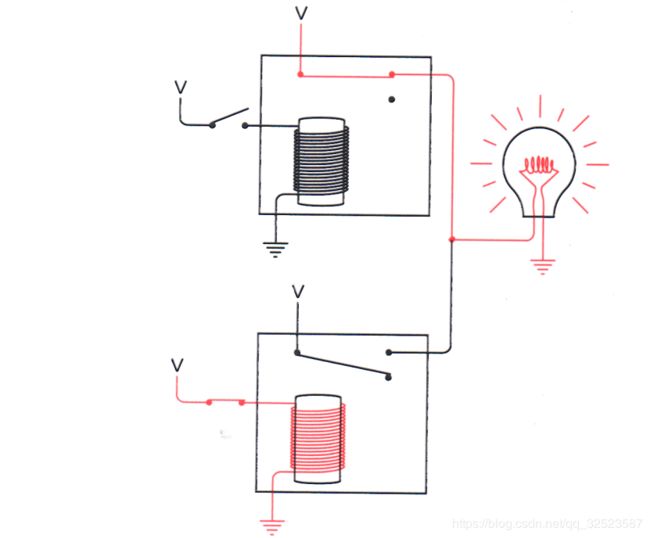
连接两个继电器的另一种方式如下图所示:
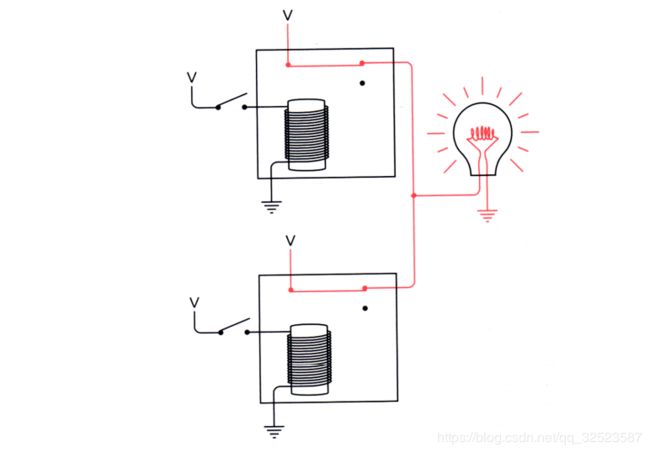
在这种情况下,两个输出连在一起。除了连在继电器的另一个触点上之外,这种连接形式与或门类似。当两个开关都断开时灯泡是亮的。
当只有上面的开关闭合时,灯泡也是亮的:
只有当两个开关都闭合时,灯泡才会熄灭:
这种行为和与门的行为正好相反,被称为“ NAND gate (与非门) ”。与非门的画法和与门的画法很相像,只是在输出端加了一个小圆圈,表示其最后的输出和与门的输出是相反的:

到此为止,我们已经看到可用四种不同的方式来连接有两个输入、一个输出的继电器,每一种方式的行为功能都不一样。为避免画继电器,我们把这些连接称为逻辑门并使用电气工程师们使用的符号来表示它们。特定的逻辑门的输出取决于其输入,总结如下:

现在已有了四个逻辑门和一个反向器,完成这些工具的其实就是原始的继电器:
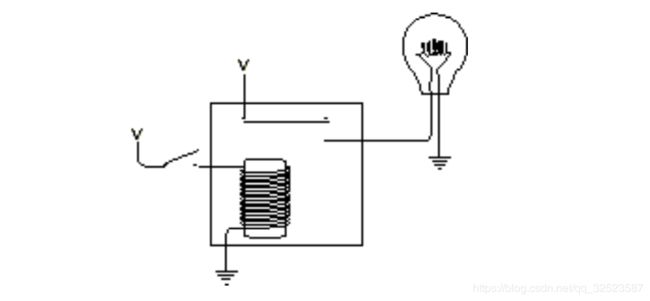
上图称为 缓冲器,用符号表示如下:![]()
它和反向器的符号类似,只是没有小圆圈。缓冲器的特点是“什么都不做”,其输出和输入是相同的:

当输入信号很弱时,可以使用缓冲器,这是因为这也正是多年前继电器被用于电报当中的原因。此外,缓冲器也可用于延迟一个信号,这是因为继电器可能要求多一点儿动作时间,如1 秒的几分之一才被触发。
本书从现在开始不再画继电器,取而代之的是电路将由缓冲器、反向器、4个基本逻辑门及更复杂的电路(如2- 4译码器)组成。当然,所有这些部件也是由继电器构成的,但我们用不着看到它了。
前面讲过,可用下面的小电路构造一个 2- 4译码器:
两个输入被反向后成为与门的输入。有时,像这样的配置可以去掉反向器而画成如下的样子:

注意与门输入端的小圆圈,这些小圆圈表示信号在这些点上被反向了, 0会变成1,而1变为0。
具有反向输入端的与门和或非门的行为是一样的:
这两对等同的电路实际上就是迪摩根定律的内容。迪摩根是维多利亚时代的另一位数学家,他比布尔年长 9 岁。据说,他的书《 Formal logic 》发表于 1 8 4 7 年,和布尔的《 T h eMathematical Analysis of logic》恰好是同一天。事实上,布尔正是由于受到发生在迪摩根和另一个英国数学家之间的剽窃事件的触动而研究逻辑的。 (迪摩根最后证明是清白的。 )很早以前,迪摩根就意识到了布尔思想的重要性。他无私地鼓励和帮助布尔进行研究,但最终除了他的这个著名的定律外,他几乎被人们遗忘了。
迪摩根定律可以简单地表示成:

A和B 是两个布尔操作数。在第一个表达式中,它们被取反(即反向)后再相与。这和先把它们相或后再取反(或非门的功能)的结果是一致的。第二个表达式中,两个操作数被取反后再相或,这和先把它们相与后再取反(与非门的功能)的结果是一样的。
迪摩根定律对于简化布尔表达式,进而简化电路是一个很重要的工具。从历史上讲,这正是香农的论文对电气工程师的真正含义。但是,专门简化电路并非本书的焦点,更重要的是让事物工作、起作用。下面我们要运行起来的就是一台简单的加法机。