算法分析与复杂性理论
1. 函数渐进的界
1.1 大 O O O 符号
-
定义:
设 f f f 和 g g g 是定义域为自然数集N上的函数。若存在正数 c c c 和 n 0 n_0 n0 ,使得对于一切 n > n 0 n > n_0 n>n0 有 0 ≤ f ( n ) ≤ c g ( n ) 0 \le f (n) \le cg(n) 0≤f(n)≤cg(n) 成立,则称 f ( n ) f (n) f(n) 的渐进上界是 g ( n ) g(n) g(n),记作:
f ( n ) = O ( g ( n ) ) f (n) = O(g(n)) f(n)=O(g(n))
自然数:自然数是指用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4……所表示的数。自然数由0开始,一个接一个,组成一个无穷的集体。自然数有有序性,无限性。分为偶数和奇数,合数和质数等。
-
说明:
- f ( n ) = O ( g ( n ) ) f (n) = O(g(n)) f(n)=O(g(n)), f ( n ) f (n) f(n) 的阶不高于 g ( n ) g(n) g(n) 的阶;
- 可能存在多个正数 c c c ,只要指出一个即可;
- 对前面有限多个值可以不满足不等式;
- 常数函数可以写作 O ( 1 ) O(1) O(1)
-
栗子:
设 f ( n ) = n 2 + n f (n) = n^2 + n f(n)=n2+n,则:- f ( n ) = O ( n 2 ) f (n) = O(n^2) f(n)=O(n2),取 c = 2 , n 0 = 1 c = 2, n_0 = 1 c=2,n0=1 即可;
- f ( n ) = O ( n 3 ) f (n) = O(n^3) f(n)=O(n3),取 c = 1 , n 0 = 2 c = 1, n_0 = 2 c=1,n0=2 即可;
1.2 大 Ω \Omega Ω 符号
-
定义:
设 f f f 和 g g g 是定义域为自然数集N上的函数。若存在正数 c c c 和 n 0 n_0 n0 ,使得对于一切 n > n 0 n > n_0 n>n0 有 0 ≤ c g ( n ) ≤ f ( n ) 0 \le cg(n) \le f (n) 0≤cg(n)≤f(n) 成立,则称 f ( n ) f (n) f(n) 的渐进下界是 g ( n ) g(n) g(n),记作:
f ( n ) = Ω ( g ( n ) ) f (n) = \Omega(g(n)) f(n)=Ω(g(n))
-
说明:
- f ( n ) = Ω ( g ( n ) ) f (n) = \Omega(g(n)) f(n)=Ω(g(n)), f ( n ) f (n) f(n) 的阶不低于 g ( n ) g(n) g(n) 的阶;
- 可能存在多个正数 c c c ,只要指出一个即可;
- 对前面有限多个值可以不满足不等式;
-
栗子:
设 f ( n ) = n 2 + n f (n) = n^2 + n f(n)=n2+n,则:
- f ( n ) = Ω ( n 2 ) f (n) = \Omega(n^2) f(n)=Ω(n2),取 c = 1 , n 0 = 1 c = 1, n_0 = 1 c=1,n0=1 即可;
- f ( n ) = Ω ( 100 n ) f (n) = \Omega(100n) f(n)=Ω(100n),取 c = 1 100 , n 0 = 1 c = \frac{1}{100}, n_0 = 1 c=1001,n0=1 即可;
1.3 小 o o o 符号
-
定义:
设 f f f 和 g g g 是定义域为自然数集N上的函数。若对于任意正数 c c c 都存在 n 0 n_0 n0,使得对于一切 n > n 0 n > n_0 n>n0 有 0 ≤ f ( n ) ≤ c g ( n ) 0 \le f (n) \le cg(n) 0≤f(n)≤cg(n) 成立,则记作:
f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n))
-
说明:
- f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n)), f ( n ) f (n) f(n) 的阶低于 g ( n ) g(n) g(n) 的阶;
- 对不同的正数 c c c, n 0 n_0 n0 不一样, c c c 越小 n 0 n_0 n0 越大;
- 对前面有限多个值可以不满足不等式;
-
栗子:
设 f ( n ) = n 2 + n f (n) = n^2 + n f(n)=n2+n,则: f ( n ) = o ( n 3 ) f (n) = o(n^3) f(n)=o(n3)
证:
-
当 c ≥ 1 c \ge 1 c≥1 时显然成立,只要取 n 0 = 2 n_0 = 2 n0=2, n 2 + n < c n 3 n^2 + n < cn^3 n2+n<cn3;
-
当 0 < c < 1 0 < c < 1 0<c<1 时,取 n 0 = ⌈ 2 c ⌉ n_0 = \left \lceil \frac{2}{c} \right \rceil n0=⌈c2⌉ 即可,因为当 n ≥ n 0 n \ge n_0 n≥n0:
c n ≥ c n 0 > 2 cn \ge cn_0 > 2 cn≥cn0>2
n 2 + n < 2 n 2 < c n 3 n^2 + n < 2n^2 < cn^3 n2+n<2n2<cn3
-
1.4 小 ω \omega ω 符号
-
定义:
设 f f f 和 g g g 是定义域为自然数集N上的函数。若对于任意正数 c c c 都存在 n 0 n_0 n0,使得对于一切 n > n 0 n > n_0 n>n0 有 $0 \le cg(n) \le f (n) $ 成立,则记作:
f ( n ) = ω ( g ( n ) ) f (n) = \omega(g(n)) f(n)=ω(g(n))
-
说明:
- f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n)), f ( n ) f (n) f(n) 的阶高于 g ( n ) g(n) g(n) 的阶;
- 对不同的正数 c c c, n 0 n_0 n0 不一样, c c c 越小 n 0 n_0 n0 越大;
- 对前面有限多个值可以不满足不等式;
1.5 Θ \Theta Θ 符号
-
定义:
若 f ( n ) = O ( g ( n ) ) f (n) = O(g(n)) f(n)=O(g(n)) 且 f ( n ) = Ω ( g ( n ) ) f (n) = \Omega(g(n)) f(n)=Ω(g(n)),则记作:
f ( n ) = Θ ( g ( n ) ) f (n) = \Theta(g(n)) f(n)=Θ(g(n))
-
说明:
- f ( n ) f (n) f(n) 的阶与 g ( n ) g(n) g(n) 的阶相同
- 对前面有限多个值可以不满足条件;
| 定义 | 说明 | |
|---|---|---|
| O O O | 设 f f f 和 g g g 是定义域为自然数集N上的函数。若存在正数 c c c 和 n 0 n_0 n0 ,使得对于一切 n > n 0 n > n_0 n>n0 有 0 ≤ f ( n ) ≤ c g ( n ) 0 \le f (n) \le cg(n) 0≤f(n)≤cg(n) 成立,则称 f ( n ) f (n) f(n) 的渐进上界是 g ( n ) g(n) g(n),记作: f ( n ) = O ( g ( n ) ) f (n) = O(g(n)) f(n)=O(g(n)) | f ( n ) = O ( g ( n ) ) f (n) = O(g(n)) f(n)=O(g(n)), f ( n ) f (n) f(n) 的阶不高于 g ( n ) g(n) g(n) 的阶; 可能存在多个正数 c c c ,只要指出一个即可; 对前面有限多个值可以不满足不等式; 常数函数可以写作 O ( 1 ) O(1) O(1) |
| Ω \Omega Ω | 设 f f f 和 g g g 是定义域为自然数集N上的函数。若存在正数 c c c 和 n 0 n_0 n0 ,使得对于一切 n > n 0 n > n_0 n>n0 有 0 ≤ c g ( n ) ≤ f ( n ) 0 \le cg(n) \le f (n) 0≤cg(n)≤f(n) 成立,则称 f ( n ) f (n) f(n) 的渐进下界是 g ( n ) g(n) g(n),记作: f ( n ) = Ω ( g ( n ) ) f (n) = \Omega(g(n)) f(n)=Ω(g(n)) | f ( n ) = Ω ( g ( n ) ) f (n) = \Omega(g(n)) f(n)=Ω(g(n)), f ( n ) f (n) f(n) 的阶不低于 g ( n ) g(n) g(n) 的阶; 可能存在多个正数 c c c ,只要指出一个即可; 对前面有限多个值可以不满足不等式; |
| o o o | 设 f f f 和 g g g 是定义域为自然数集N上的函数。若对于任意正数 c c c 都存在 n 0 n_0 n0,使得对于一切 n > n 0 n > n_0 n>n0 有 0 ≤ f ( n ) ≤ c g ( n ) 0 \le f (n) \le cg(n) 0≤f(n)≤cg(n) 成立,则记作: f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n)) | f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n)), f ( n ) f (n) f(n) 的阶低于 g ( n ) g(n) g(n) 的阶; 对不同的正数 c c c, n 0 n_0 n0 不一样, c c c 越小 n 0 n_0 n0 越大; 对前面有限多个值可以不满足不等式; |
| ω \omega ω | 设 f f f 和 g g g 是定义域为自然数集N上的函数。若对于任意正数 c c c 都存在 n 0 n_0 n0,**使得对于一切 n > n 0 n > n_0 n>n0 有 $0 \le cg(n) \le f (n) ∗ ∗ 成 立 , 则 记 作 : ** 成立,则记作: ∗∗成立,则记作:f (n) = \omega(g(n))$ | f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n)), f ( n ) f (n) f(n) 的阶高于 g ( n ) g(n) g(n) 的阶; 对不同的正数 c c c, n 0 n_0 n0 不一样, c c c 越小 n 0 n_0 n0 越大; 对前面有限多个值可以不满足不等式; |
| Θ \Theta Θ | 若 f ( n ) = O ( g ( n ) ) f (n) = O(g(n)) f(n)=O(g(n)) 且 f ( n ) = Ω ( g ( n ) ) f (n) = \Omega(g(n)) f(n)=Ω(g(n)),则记作: f ( n ) = Θ ( g ( n ) ) f (n) = \Theta(g(n)) f(n)=Θ(g(n)) | f ( n ) f (n) f(n) 的阶与 g ( n ) g(n) g(n) 的阶相同 对前面有限多个值可以不满足条件; |
2. 函数渐进界的定理
2.1 定理1:Knowledge
-
定理内容:
设 f f f 和 g g g 是定义域为自然数集合的函数。
-
如果 lim n → ∞ f ( n ) g ( n ) \lim_{n \to \infty}\frac{f (n)}{g(n)} limn→∞g(n)f(n) 存在,并且等于某个常数 c > 0 c > 0 c>0 ,那么:
f ( n ) = Θ ( g ( n ) ) f (n) = \Theta(g(n)) f(n)=Θ(g(n))
-
如果 lim n → ∞ f ( n ) g ( n ) = 0 \lim_{n \to \infty}\frac{f (n)}{g(n)} = 0 limn→∞g(n)f(n)=0 ,那么:
f ( n ) = o ( g ( n ) ) f (n) = o(g(n)) f(n)=o(g(n))
-
如果 lim n → ∞ f ( n ) g ( n ) = + ∞ \lim_{n \to \infty}\frac{f (n)}{g(n)} = +\infty limn→∞g(n)f(n)=+∞ ,那么:
f ( n ) = ω ( g ( n ) ) f (n) = \omega(g(n)) f(n)=ω(g(n))
-
-
栗子:
设 f ( n ) = 1 2 n 2 − 3 n f (n) = \frac{1}{2}n^2 - 3n f(n)=21n2−3n,证明 f ( n ) = Θ ( n 2 ) f (n) = \Theta(n^2) f(n)=Θ(n2)
证:因为
lim n → ∞ f ( n ) n 2 = lim n → ∞ 1 2 n 2 − 3 n n 2 = 1 2 \lim_{n \to \infty}\frac{f (n)}{n^2} = \lim_{n \to \infty}\frac{\frac{1}{2}n^2 - 3n}{n^2} = \frac{1}{2} limn→∞n2f(n)=limn→∞n221n2−3n=21
根据定理1,有 f ( n ) = Θ ( n 2 ) f (n) = \Theta(n^2) f(n)=Θ(n2)
-
根据定理1,得到的一些重要的结论:
- n d = o ( r n ) , r > 1 , d > 0 n^d = o(r^n), r > 1, d > 0 nd=o(rn),r>1,d>0 => 多项式函数的阶低于指数函数的阶
- ln n = o ( n d ) , d > 0 \ln n = o(n^d), d > 0 lnn=o(nd),d>0 => 对数函数的阶低于幂函数的阶
2.2 定理2:
-
定理内容:
设 f , g , h f, g, h f,g,h 的定义域为自然数集合:(函数阶之间的关系具有可传递性)
- 如果 f = O ( g ) f = O(g) f=O(g),且 f = O ( h ) f = O(h) f=O(h),那么 f = O ( h ) f = O(h) f=O(h);
- 如果 f = Ω ( g ) f = \Omega(g) f=Ω(g),且 f = Ω ( h ) f = \Omega(h) f=Ω(h),那么 f = Ω ( h ) f = \Omega(h) f=Ω(h);
- 如果 f = Θ ( g ) f = \Theta(g) f=Θ(g),且 f = Θ ( h ) f = \Theta(h) f=Θ(h),那么 f = Θ ( h ) f = \Theta(h) f=Θ(h);
2.3 定理3:
-
定理内容:
设 f f f 和 g g g 是定义域为自然数集合的函数,若对某个其它的函数 h h h ,有 f = O ( h ) f = O(h) f=O(h) 和 g = O ( h ) g = O(h) g=O(h),那么:
f + g = O ( h ) f + g = O(h) f+g=O(h)
=> 该性质可以推广到有限个函数
-
算法的时间复杂度是各步操作时间之和,在常数步的情况下取最高阶的函数即可。
4. 基本函数
4.1 对数函数
- 符号:
- log n = log 2 n \log n = \log_2 n logn=log2n
- log k n = ( log n ) k \log^k n = (\log n)^k logkn=(logn)k
- log log n = log ( log n ) \log\log n = \log(\log n) loglogn=log(logn)
- 性质:
- log 2 n = Θ ( log l n ) \log_2 n = \Theta(\log_l n) log2n=Θ(logln)
- l o g b n = o ( n α ) , α > 0 log_b n = o(n^\alpha), \alpha > 0 logbn=o(nα),α>0
- $\alpha ^{\log_b n} = n^{\log_b \alpha} $
4.2 指数函数与阶乘
-
斯特林公式(Stirling):
n ! = 2 π n ( n e ) n ( 1 + Θ ( 1 n ) ) n! = \sqrt{2\pi n}(\frac{n}{e})^n(1 + \Theta(\frac{1}{n})) n!=2πn(en)n(1+Θ(n1))
-
由 Stirling 公式得到的结论:
- n ! = o ( n n ) n! = o(n^n) n!=o(nn)
- n ! = ω ( 2 n ) n! = \omega(2^n) n!=ω(2n)
- log ( n ! ) = Θ ( n log n ) \log(n!) = \Theta(n\log n) log(n!)=Θ(nlogn)
-
log ( n ! ) = Θ ( n log n ) \log(n!) = \Theta(n\log n) log(n!)=Θ(nlogn) 证明:
Knowledge-
log ( n ! ) = Ω ( n log n ) \log(n!) = \Omega(n\log n) log(n!)=Ω(nlogn) 的证明:
log ( n ! ) = ∑ k = 1 n log k ≥ ∫ 1 n log x d x = log e ( n ln n − n + 1 ) = Ω ( n log n ) \log(n!) = \sum_{k = 1}^n\log k \ge \int_1^n \log x dx = \log e(n\ln n - n + 1) = \Omega(n\log n) log(n!)=∑k=1nlogk≥∫1nlogxdx=loge(nlnn−n+1)=Ω(nlogn)
-
log ( n ! ) = O ( n log n ) \log(n!) = O(n\log n) log(n!)=O(nlogn) 的证明:
log ( n ! ) = ∑ k = 1 n log k ≤ ∫ 2 n + 1 log x d x = log e ( n ln n − n + 1 ) = O ( n log n ) \log(n!) = \sum_{k = 1}^n\log k \le \int_{2}^{n + 1} \log x dx = \log e(n\ln n - n + 1) = O(n\log n) log(n!)=∑k=1nlogk≤∫2n+1logxdx=loge(nlnn−n+1)=O(nlogn)
-
4.3 取整函数
- 定义:
- ⌊ x ⌋ \left \lfloor x \right \rfloor ⌊x⌋ :表示小于等于x的最大整数
- ⌈ x ⌉ \left \lceil x \right \rceil ⌈x⌉ :表示大于等于x的最大整数
- 性质:
- x − 1 < ⌊ x ⌋ ≤ x ≤ ⌈ x ⌉ < x + 1 x - 1 < \left \lfloor x \right \rfloor \le x \le \left \lceil x \right \rceil < x + 1 x−1<⌊x⌋≤x≤⌈x⌉<x+1
- ⌊ x + n ⌋ = ⌊ x ⌋ + n , ⌈ x + n ⌉ = ⌈ x ⌉ + n \left \lfloor x + n \right \rfloor = \left \lfloor x \right \rfloor + n, \left \lceil x + n \right \rceil = \left \lceil x \right \rceil + n ⌊x+n⌋=⌊x⌋+n,⌈x+n⌉=⌈x⌉+n
- ⌈ n 2 ⌉ + ⌊ n 2 ⌋ = n \left \lceil \frac{n}{2} \right \rceil + \left \lfloor \frac{n}{2} \right \rfloor = n ⌈2n⌉+⌊2n⌋=n
- ⌈ ⌈ n a ⌉ b ⌉ = ⌈ n a b ⌉ , ⌊ ⌊ n a ⌋ b ⌋ = ⌊ n a b ⌋ \left \lceil \frac{\left \lceil \frac{n}{a} \right \rceil}{b} \right \rceil = \left \lceil \frac{n}{ab} \right \rceil, \left \lfloor \frac{\left \lfloor \frac{n}{a} \right \rfloor}{b} \right \rfloor = \left \lfloor \frac{n}{ab} \right \rfloor ⌈b⌈an⌉⌉=⌈abn⌉,⌊b⌊an⌋⌋=⌊abn⌋
4.4 按照阶排序 Knowledge
2 2 n , n ! , n 2 n , ( 3 2 ) n , ( log n ) log n = n log log n 2^{2^n}, n!, n2^n, (\frac{3}{2})^n, (\log n)^{\log n} = n^{\log\log n} 22n,n!,n2n,(23)n,(logn)logn=nloglogn
n 3 , log ( n ! ) = Θ ( n log n ) , n = 2 log n n^3, \log{(n!)} = \Theta(n\log n), n = 2^{\log n} n3,log(n!)=Θ(nlogn),n=2logn
log 2 n , log n , log n , log log n \log^2n, \log n, \sqrt{\log n}, \log\log n log2n,logn,logn,loglogn
n 1 log n = 1 n^{\frac{1}{\log n}} = 1 nlogn1=1
5. 序列求和的方法
5.1 引例
( 1 ) . ∑ k = 1 n − 1 1 k ( k + 1 ) = ∑ k = 1 n − 1 ( 1 k − 1 k + 1 ) = ∑ k = 1 n − 1 1 k − ∑ k = 1 n − 1 1 k + 1 = ∑ k = 1 n − 1 1 k − ∑ k = 2 n 1 k = 1 − 1 n \begin{aligned}(1). \sum_{k = 1}^{n - 1}\frac{1}{k(k + 1)}&=\sum_{k = 1}^{n - 1}(\frac{1}{k} - \frac{1}{k + 1})\\ &=\sum_{k = 1}^{n - 1}\frac{1}{k} - \sum_{k = 1}^{n - 1}\frac{1}{k + 1}\\ &=\sum_{k = 1}^{n - 1}\frac{1}{k} - \sum_{k = 2}^{n}\frac{1}{k} \\ &= 1 - \frac{1}{n} \\ \end{aligned} (1).k=1∑n−1k(k+1)1=k=1∑n−1(k1−k+11)=k=1∑n−1k1−k=1∑n−1k+11=k=1∑n−1k1−k=2∑nk1=1−n1
( 2 ) . ∑ t = 1 k t 2 t − 1 = ∑ t = 1 k t ( 2 t − 2 t − 1 ) = ∑ t = 1 k t 2 t − ∑ t = 1 k t 2 t − 1 = ∑ t = 1 k t 2 t − ∑ t = 0 k − 1 ( t + 1 ) 2 t = ∑ t = 1 k t 2 t − ∑ t = 0 k − 1 t 2 t − ∑ t = 0 k − 1 2 t = k 2 t − ( 2 k − 1 ) = ( k − 1 ) 2 k + 1 \begin{aligned}(2). \sum_{t = 1}^{k}t2^{t - 1}&=\sum_{t = 1}^{k}t(2^t - 2^{t - 1}) \\ &=\sum_{t = 1}^{k}t2^t - \sum_{t = 1}^{k}t2^{t - 1} \\ &=\sum_{t = 1}^{k}t2^t - \sum_{t = 0}^{k - 1}(t + 1)2^t \\ &=\sum_{t = 1}^{k}t2^t - \sum_{t = 0}^{k - 1}t2^t - \sum_{t = 0}^{k - 1}2^t \\ &=k2^t - (2^k - 1) = (k - 1)2^k + 1\\ \end{aligned} (2).t=1∑kt2t−1=t=1∑kt(2t−2t−1)=t=1∑kt2t−t=1∑kt2t−1=t=1∑kt2t−t=0∑k−1(t+1)2t=t=1∑kt2t−t=0∑k−1t2t−t=0∑k−12t=k2t−(2k−1)=(k−1)2k+1
5.2 二分检索的平均时间复杂度 knowledge
A ( n ) = ⌊ log n ⌋ + 1 2 A(n) = \left \lfloor \log n \right \rfloor + \frac{1}{2} A(n)=⌊logn⌋+21
5.3 估计和式上界的放大法 knowledge
-
两个放大公式:
-
∑ k = 1 n a k ≤ n a m a x \sum_{k = 1}^n a_k \le na_{max} ∑k=1nak≤namax
-
假设存在常数 r < 1 r < 1 r<1 ,使得对一切 k ≥ 0 k \ge 0 k≥0 有 a k + 1 a k ≤ r \frac{a_{k + 1}}{a_k} \le r akak+1≤r 成立,则有如下结论:
∑ k = 0 n ≤ ∑ k = 0 ∞ a 0 r k = a 0 ∑ k = 0 ∞ r k = a 0 1 − r \sum_{k = 0}^n \le \sum_{k = 0}^\infty a_0r^k = a_0\sum_{k = 0}^\infty r^k = \frac{a_0}{1 - r} ∑k=0n≤∑k=0∞a0rk=a0∑k=0∞rk=1−ra0
-
-
栗子:
估计 ∑ k = 1 n k 3 k \sum_{k = 1}^n \frac{k}{3^k} ∑k=1n3kk 的上界。
解:
∑ k = 1 n k 3 k = ∑ k = 0 n k 3 k \sum_{k = 1}^n \frac{k}{3^k} = \sum_{k = 0}^{n}\frac{k}{3^{k}} ∑k=1n3kk=∑k=0n3kk
令 a k = k 3 k , a k + 1 = k + 1 3 k + 1 a_k = \frac{k}{3^{k}}, a_{k + 1} = \frac{k + 1}{3^{k + 1}} ak=3kk,ak+1=3k+1k+1,则 a k + 1 a k = ( k + 1 ) 3 k ( k ) 3 k + 1 = k + 1 3 k ≤ 2 3 ( k > = 1 ) \frac{a_{k + 1}}{a_k} = \frac{(k + 1)3^{k}}{(k)3^{k + 1}} = \frac{k + 1}{3k} \le \frac{2}{3} (k >= 1) akak+1=(k)3k+1(k+1)3k=3kk+1≤32(k>=1)
所以,由上述第二个放大公式有:
∑ k = 1 n k 3 k ≤ ∑ k = 1 ∞ 1 3 ( 2 3 ) k − 1 = 1 3 1 1 − 2 3 = 1 \sum_{k = 1}^n \frac{k}{3^k} \le \sum_{k = 1}^\infty \frac{1}{3}(\frac{2}{3})^{k - 1} = \frac{1}{3}\frac{1}{1 - \frac{2}{3}} = 1 ∑k=1n3kk≤∑k=1∞31(32)k−1=311−321=1
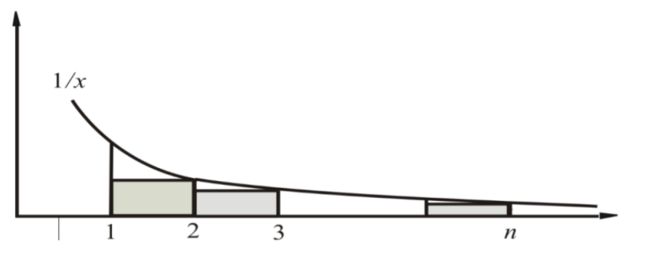
5.4 估计和式渐进的界 Knowledge
估计 ∑ k = 1 n 1 k \sum_{k = 1}^n \frac{1}{k} ∑k=1nk1 的渐进的界
-
∑ k = 1 n 1 k ≥ ∫ 1 n + 1 d x x = ln ( n + 1 ) \sum_{k = 1}^n \frac{1}{k} \ge \int_1^{n + 1}\frac{dx}{x} = \ln (n + 1) ∑k=1nk1≥∫1n+1xdx=ln(n+1)
-
∑ k = 1 n 1 k = 1 1 + ∑ k = 2 n 1 k ≤ 1 + ∫ 1 n d x x = ln n + 1 \sum_{k = 1}^n \frac{1}{k} = \frac{1}{1} + \sum_{k = 2}^n \frac{1}{k} \le 1 + \int_1^{n}\frac{dx}{x} = \ln n + 1 ∑k=1nk1=11+∑k=2nk1≤1+∫1nxdx=lnn+1
所以, ∑ k = 1 n 1 k = Θ ( ln n ) = Θ ( log n ) \sum_{k = 1}^n \frac{1}{k} = \Theta(\ln n) = \Theta(\log n) ∑k=1nk1=Θ(lnn)=Θ(logn)
6. 递推方程与算法分析 Knowledge
-
主定理的应用背景:
T ( n ) = a T ( n b ) + f ( n ) T(n) = aT(\frac{n}{b}) + f (n) T(n)=aT(bn)+f(n)
- a a a :规约后的子问题个数
- $\frac{n}{b} $ :规约后子问题的规模
- f ( n ) f (n) f(n) :规约过程以及组合子问题的解的工作量
二分检索 => T ( n ) = T ( n 2 ) + 1 T(n) = T(\frac{n}{2}) + 1 T(n)=T(2n)+1
二分归并排序 => T ( n ) = 2 T ( n 2 ) + n − 1 T(n) = 2T(\frac{n}{2}) + n - 1 T(n)=2T(2n)+n−1
-
主定理:
设 a > 1 , b > 1 a > 1, b > 1 a>1,b>1 为常数, f ( n ) f (n) f(n) 为函数, T ( n ) T(n) T(n) 为非负整数,且 T ( n ) = a T ( n b ) + f ( n ) T(n) = aT(\frac{n}{b}) + f (n) T(n)=aT(bn)+f(n),则:
-
若 f ( n ) = O ( n l o g b a − ϵ ) f (n) = O(n^{log_b a - \epsilon}) f(n)=O(nlogba−ϵ), ϵ > 0 \epsilon > 0 ϵ>0 ,那么:
T ( n ) = Θ ( n log b a ) T(n) = \Theta(n^{\log_b a}) T(n)=Θ(nlogba)
-
若 f ( n ) = Θ ( n l o g b a ) f (n) = \Theta(n^{log_b a}) f(n)=Θ(nlogba),那么:
T ( n ) = Θ ( n log b a log n ) T(n) = \Theta(n^{\log_b a}\log n) T(n)=Θ(nlogbalogn)
-
若 f ( n ) = Ω ( n log b a + ϵ ) f (n) = \Omega(n^{\log_b a + \epsilon}) f(n)=Ω(nlogba+ϵ), ϵ > 0 \epsilon > 0 ϵ>0,且对于某个常数 c < 1 c < 1 c<1 和充分大的 n n n 有 a f ( n b ) ≤ c f ( n ) af(\frac{n}{b}) \le cf (n) af(bn)≤cf(n),那么:
T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f (n)) T(n)=Θ(f(n))
-
-
例1:
求解递推方程: T ( n ) = 9 T ( n 3 ) + n T(n) = 9T(\frac{n}{3}) + n T(n)=9T(3n)+n
解:
a = 9 , b = 3 , f ( n ) = n a = 9, b = 3, f (n) = n a=9,b=3,f(n)=n
n log b a = n l o g 3 9 = n 2 n^{\log_b a} = n^{log_3 9} = n^2 nlogba=nlog39=n2, f ( n ) = O ( n l o g 3 9 − 1 ) f (n) = O(n^{log_3 9 - 1}) f(n)=O(nlog39−1)
根据主定理规则1,其中 ϵ = 1 \epsilon = 1 ϵ=1:
T ( n ) = Θ ( n 2 ) T(n) = \Theta(n^2) T(n)=Θ(n2)
-
例2:
求解递推方程: T ( n ) = T ( 2 n 3 ) + 1 T(n) = T(\frac{2n}{3}) + 1 T(n)=T(32n)+1
解:
a = 1 , b = 3 2 , f ( n ) = 1 a = 1, b = \frac{3}{2}, f (n) = 1 a=1,b=23,f(n)=1
n l o g b a = n l o g 3 2 1 = 1 n^{log_b a} = n^{log_{\frac{3}{2}} 1} = 1 nlogba=nlog231=1 , f ( n ) = n l o g 3 2 1 f (n) = n^{log_{\frac{3}{2}}1} f(n)=nlog231
根据主定理规则2:
T ( n ) = Θ ( n log 3 2 1 log n ) = Θ ( log n ) T(n) = \Theta(n^{\log_{\frac{3}{2}} 1} \log n) = \Theta(\log n) T(n)=Θ(nlog231logn)=Θ(logn)
-
例3:
求解递推方程: T ( n ) = 3 T ( n 4 ) + n log n T(n) = 3T(\frac{n}{4}) + n\log n T(n)=3T(4n)+nlogn
解:
a = 3 , b = 4 , f ( n ) = n log n a = 3, b = 4, f (n) = n\log n a=3,b=4,f(n)=nlogn
n log b a = n log 4 3 ≈ 0.793 n^{\log_b a} = n^{\log_4 3} \approx 0.793 nlogba=nlog43≈0.793
取 ϵ = 0.2 \epsilon = 0.2 ϵ=0.2,则 f ( n ) = n log n = Ω ( n log 4 3 + 0.2 ) f (n) = n\log n = \Omega(n^{\log_4 3 + 0.2}) f(n)=nlogn=Ω(nlog43+0.2) = Ω ( n 0.993 ) \Omega(n^{0.993}) Ω(n0.993)
条件验证:要使 a f ( n b ) ≤ c f ( n ) af(\frac{n}{b}) \le cf (n) af(bn)≤cf(n) 成立,带入 f ( n ) = n log n f (n) = n\log n f(n)=nlogn 得到:
3 ( n 4 ) log ( n 4 ) ≤ c n log n 3(\frac{n}{4})\log (\frac{n}{4}) \le cn\log n 3(4n)log(4n)≤cnlogn
当 c ≥ 3 4 c \ge \frac{3}{4} c≥43 时,上述不等式可以对充分打的n成立,根据主定理规则3:
T ( n ) = Θ ( f ( n ) ) = Θ ( n log n ) T(n) = \Theta(f (n)) = \Theta(n\log n) T(n)=Θ(f(n))=Θ(nlogn)
-
二分检索:
W ( n ) = W ( n 2 ) + 1 , W ( 1 ) = 1 W(n) = W(\frac{n}{2}) + 1, W(1) = 1 W(n)=W(2n)+1,W(1)=1
解:
a = 1 , b = 2 , f ( n ) = 1 , n log 2 1 = 1 a = 1, b = 2, f (n) = 1, n^{\log_2 1} = 1 a=1,b=2,f(n)=1,nlog21=1
根据主定理规则2:
W ( n ) = Θ ( log n ) W(n) = \Theta(\log n) W(n)=Θ(logn)
-
二分归并排序:
W ( n ) = 2 W ( n 2 ) + n − 1 , W ( 1 ) = 0 W(n) = 2W(\frac{n}{2}) + n - 1, W(1) = 0 W(n)=2W(2n)+n−1,W(1)=0
解:
a = 2 , b = 2 , f ( n ) = n − 1 , n log 2 2 = n a = 2, b = 2, f (n) = n - 1, n^{\log_2 2} = n a=2,b=2,f(n)=n−1,nlog22=n 根据主定理规则2:
W ( n ) = Θ ( n log n ) W(n) = \Theta(n\log n) W(n)=Θ(nlogn)
-
例4: => 不能使用主定理的情形
求解递推方程: T ( n ) = 2 T ( n 2 ) + n log n T(n) = 2T(\frac{n}{2}) + n\log n T(n)=2T(2n)+nlogn
解:
a = 2 , b = 2 , f ( n ) = n log n , n log b a = n a = 2, b = 2, f (n) = n\log n, n^{\log_b a} = n a=2,b=2,f(n)=nlogn,nlogba=n
不存在 ϵ > 0 \epsilon > 0 ϵ>0 使得: n log n = Ω ( n 1 + ϵ ) n\log n = \Omega(n^{1 + \epsilon}) nlogn=Ω(n1+ϵ)
不存在 c < 1 c < 1 c<1 使 a f ( n b ) ≤ c f ( n ) af(\frac{n}{b}) \le cf (n) af(bn)≤cf(n) 对所有充分大的 n n n 成立
2 ( n 2 ) log n 2 = n ( log n − 1 ) ≤ c n log n 2(\frac{n}{2})\log{\frac{n}{2}} = n(\log n - 1) \le cn\log n 2(2n)log2n=n(logn−1)≤cnlogn