二叉树之一BST树,AVL树详解及B树和红黑树原理分析
转载:https://blog.csdn.net/yanerhao/article/details/61198487
BST树,AVL树详解及B树和红黑树原理分析
互联网面试中树尤其是BST,AVL是提问的重点也是难点,甚至B树乃至高级数据结构红黑树都是提问的重点,像阿里云面试就曾经问过map实现机制(红黑树)及其原理,这里我们要做到对BST/AVL完全熟悉能给出全部代码实现,红黑树、b树之类,有能力的需要完全理解,代码就不用掌握了。红黑树和b树看会就行了,当碰到你感觉他们不懂这方面的面试官的时候,可以逮着他们狂扯这部分,然后让他们感觉你很高大上。
以二叉树或者树作为表的组织形式,称为树表。树表在进行增删操作时可以方便维护表有序,不需要移动记录,比顺序存储的表效率要高,开销要低。常见树表BST/AVL,B树等。
一 二查搜索树BST
二叉排序树BST其定义:
1 首先它也是一个二叉树,故满足递归定义;
2 其次每个节点只存在一个值;
3 需满足左子树值<=根值<=右子树,故按照中序遍历会得到一个非递减序列。
![]()
BST涉及操作主要增,删,查,除了删麻烦一点,其他操作均可递归实现,二叉查找树的一般性质:1.在一棵二叉查找树上,执行查找、插入、删除等操作,的时间复杂度为O(lgn)。因为,一棵由n个结点,随机构造的二叉查找树的高度为lgn,所以顺理成章,一般操作的执行时间为O(lgn)。2.但若是一棵具有n个结点的线性链,则此些操作最坏情况运行时间为O(n)。
代码:
-
struct node{
-
int key;
-
node*left;
-
node*right;
-
};
-
int bstinsert(node*&p,int k){
-
if(p==
NULL){p=(node*)
malloc(
sizeof(node));p->key=k;p->left=p->right=
NULL;
return
1;}
-
else {
if(k==p->key)
return
0;
-
else
if(k
key)
return bstinsert(p->left,k);
-
else
return bstinsert(p->right,k);
-
}
-
}
-
void bstcreate(node*&r,int a[],int n)
-
{
-
int i;
-
r==
NULL;
-
for(i=
0;i
-
bstinsert(r,a[i]);
-
}
-
node* bstsearch(node*root,int k){
-
if(root==
NULL)
return root;
-
else
if(k==root->key)
return root;
-
else
if(k
key)
return bstsearch(root->left,k);
-
else
return bstsearch(root->right,k);
-
}
-
int bstdelete(node*&root,int k){
-
node *p=root,*pa,*r;
-
pa=
NULL;
//父节点
-
while(p&&p->key!=k){
-
pa=p;
-
if(p->key>k)p=p->left;
-
else p=p->right;
-
}
-
if(p==
NULL)
//没有找到k
-
{
cout<<
"Not Found!"<<
endl;
return
0;}
-
//分四种情况讨论
-
if(p->left==
NULL&p->right==
NULL){
-
if(pa==
NULL)root=
NULL;
-
else
if(pa->left==p)pa->left=
NULL;
-
else pa->right=
NULL;
-
delete p;}
//叶子直接删除
-
else
if(p->left==
NULL){
-
if(pa==
NULL)root=p->right;
//p是根节点
-
else
if(pa->left==p){pa->left=p->right;
delete p;}
//p是父节点左孩子,则用其右孩子取代
-
else {pa->right=p->right;
delete p;}
//p是父节点右孩子,则用其右孩子取代
-
}
//只含右节点
-
else
if(p->right==
NULL){
-
if(pa==
NULL)root=p->left;
//p是根节点
-
else
if(pa->left==p){pa->left=p->left;
delete p;}
//p是父节点左孩子,则用其右孩子取代
-
else {pa->right=p->left;
delete p;}
//p是父节点右孩子,则用其右孩子取代
-
}
//只含左节点
-
else {
-
//需要找左子树最左下或者右子树最左下孩子r取代p故先找到r
-
node*p1=p;r=p->left;
-
while(r->right){p1=r;r=r->right;}
-
//找到r节点,且该节点一定无右子树,符合上面的无右子树情况
-
if(p1->left==r){p1->left=r->left;}
-
else
if(p1->right==r){p1->right=r->left;}
-
//删除r后再把r替代p
-
r->left=p->left;
-
r->right=p->right;
-
if(pa==
NULL)root=r;
-
else
if(pa->left==p)pa->left=r;
-
else pa->right=r;
-
delete p;
-
}
//既有左孩子又有右孩子
-
p=
NULL;
-
return
1;
-
}
-
void inorder(node*r){
-
if(r){
-
inorder(r->left);
-
cout<
key<<
" ";
-
inorder(r->right);
-
}
-
}
-
void bstdis(node *r){
-
inorder(r);
-
cout<<
endl;
-
}
特点:就时间复杂度来说,BST的查找与二分查找性能差不多,但是增删时BST无需移动记录,只需移动指针比顺序存储好很多;一般性能都在O(log n)。
缺点:面对序列原本就是顺序:
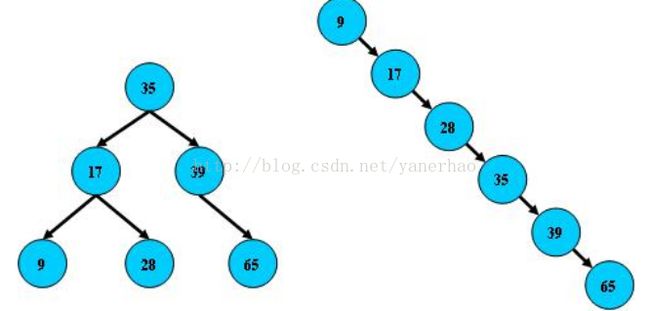
如右边顺序序列所示,此时性能和顺序存储无异。所以,使用BST树还要考虑尽可能让BST树保持左图的结构,和避免右图的结构,也就是所谓的“平衡”问题j 进而引出AVL。
二 平衡二叉树AVL
平衡二叉树AVL是带有平衡条件的BST,这个平衡条件必须容易保持,且需要保持树的深度O(log N),一般想法是要求每个节点都必须要有相同高度,但是这样要求太严格,难以实现,故退一步引出AVL:
1 首先仍是一棵二叉树,满足递归定义;
2 其次又是一棵BST,满足有序;
3 每个节点左右子树高度差的绝对值不能超过1
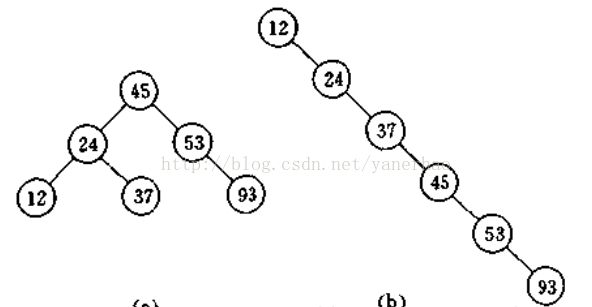
AVL树各节点的平衡因子定义为左子树深度减去右子树深度,AVL的平衡因子一般都只能-1,0,1,当绝对值大于1时则AVL失去平衡。例如在完成插入后,失衡只有那些从插入点到根节点路径上的平衡可能被打破,当沿着这条路径上溯到根,找到插入新节点后失去平衡的最小子树根节点的指针x,然后再调整这个子树使之重新平衡。注意当失去平衡的最小子树(这样的最小子树指的是离插入点最近)调整平衡后,原有的其他所有不平衡树无需调整,整个二叉树回归平衡,使得BST操作性能始终维持在对数级别。这种调整所需要的主要技术就是旋转,下面具体介绍:
1 插入点位于x的左孩子的左子树中--左左LL;
2 插入点位于x的左孩子的右子树-中-左右LR;
3 插入点位于x的右孩子的左子树-中-右左RL;
4 插入点位于x的右孩子的右子树-中-右右RR;
1和4是对称的,成为外侧插入,通过单旋转解决;2和3是对称的,成为内侧插入,通过单旋转解决。
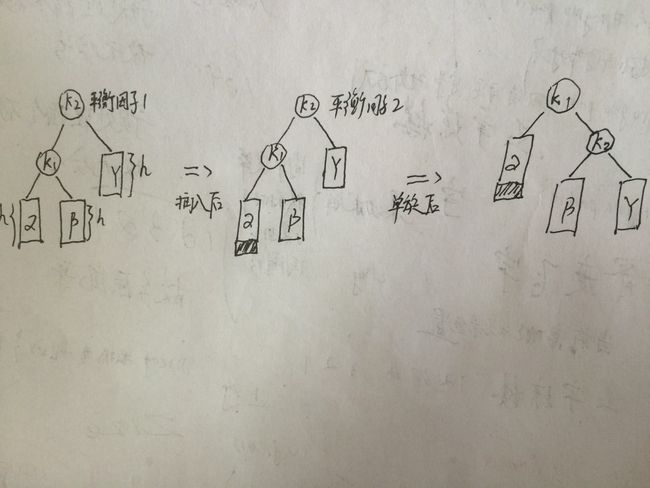
1 LL型调整(右旋)
设最深节点k2,最深节点左孩子k1,在k1左子树再插入一个新节点,使得k2平衡因子大于1不平衡,如图,k2原始平衡因子为1,矩形代表一个高度h的子树,带阴影方框为插入的一个节点,采用的方法单向右转:
-
class avlnode{
-
private:
-
int key;
-
int height;
-
int freq;
-
avlnode*left;
-
avlnode*right;
-
avlnode(
int h=
1):left(
NULL),right(
NULL),height(h),freq(
1){}
-
};
-
int get_height(avlnode *r){
-
if(r)
return r->height;
-
else
return
0;
-
}
-
void singlerotate_left(avlnode *&r){
-
avlnode *k2=r;
-
avlnode *k1=k2->left;
-
k2->left=k1->right;
-
k1->right=k2;
-
k2->height=max(get_height(k2->left),get_height(k2->right))+
1;
-
k1->height=max(get_height(k1->left),get_height(k1->right))+
1;
-
}
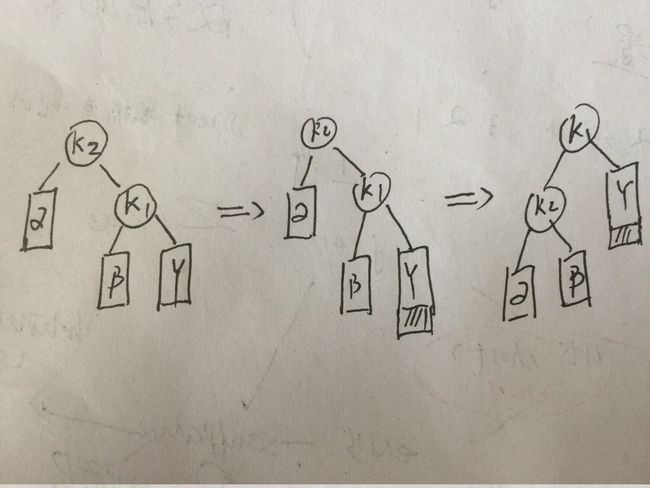
2 RR型调整
如图,采用方法单向左旋:
-
void singlerotate_right(avlnode*&r){
-
avlnode*k2=r;
-
avlnode*k1=k2->right;
-
k2->right=k1->left;
-
k1->left=k2;
-
k2->height=max(get_height(k2->left),get_height(k2->right))+
1;
-
k1->height=max(get_height(k1->left),get_height(k1->right))+
1;
-
}
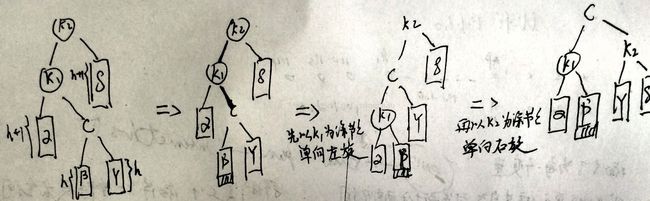
3 LR型调整
此时在最深节点k2的左孩子k1的右子树插入节点,使得k2平衡因子大于1,调整的方法是先单向左旋即将k2,最后单向右旋:
-
void doubleLeft_right(avlnode*&r){
-
avlnode*k2=r;
-
avlnode*k1=r->left;
-
singlerotate_right(k1);
-
singlerotate_left(k2);
-
}
4 RL型调整
类似LR型直接贴出代码就行。
-
void doubleright_left(avlnode*&r){
-
avlnode*k2=r;
-
avlnode*k1=r->right;
-
singlerotate_left(k1);
-
singlerotate_right(k2);
-
}
相应增删查操作如下:
注意增加操作类似BST,只不过在完成插入后需要进行调整;查找操作一样;删除操作也分为几种情况:
首先在树中搜寻是否有节点的元素值等于需要删除的元素。如未搜索到,直接返回。否则执行以下操作。
(1)要删除的节点是当前根节点T。如果左右子树都非空。在高度较大的子树中实施删除操作。分两种情况:A、左子树高度大于右子树高度,将左子树中最大的那个元素赋给当前根节点,然后删除左子树中元素值最大的那个节点。B、左子树高度小于右子树高度,将右子树中最小的那个元素赋给当前根节点,然后删除右子树中元素值最小的那个节点。如果左右子树中有一个为空,那么直接用那个非空子树或者是NULL替换当前根节点即可。
(2)要删除的节点元素值小于当前根节点T值,在左子树中进行删除。递归调用,在左子树中实施删除。这个是需要判断当前根节点是否仍然满足平衡条件,如果满足平衡条件,只需要更新当前根节点T的高度信息。否则,需要进行旋转调整:如果T的左子节点的左子树的高度大于T的左子节点的右子树的高度,进行相应的单旋转。否则进行双旋转。(3)要删除的节点元素值大于当前根节点T值,在右子树中进行删除。过程与上述步骤类似。
代码:
-
//AVL
-
int max1(int x,int y){
-
return (x>y? x:y);
-
}
-
class avlnode{
-
public:
-
int key;
-
int height;
-
int freq;
-
avlnode*left;
-
avlnode*right;
-
avlnode(
int h=
0):left(
NULL),right(
NULL),height(h),freq(
1){}
-
};
-
int get_height(avlnode *r){
-
if(r)
return r->height;
-
else
return
0;
-
}
-
avlnode* singlerotate_left(avlnode *k2){
-
avlnode *k1=k2->left;
-
k2->left=k1->right;
-
k1->right=k2;
-
k2->height=max1(get_height(k2->left),get_height(k2->right))+
1;
-
k1->height=max1(get_height(k1->left),get_height(k1->right))+
1;
-
return k1;
-
}
-
avlnode* singlerotate_right(avlnode*k2){
-
avlnode*k1=k2->right;
-
k2->right=k1->left;
-
k1->left=k2;
-
k2->height=max1(get_height(k2->left),get_height(k2->right))+
1;
-
k1->height=max1(get_height(k1->left),get_height(k1->right))+
1;
-
return k1;
-
}
-
avlnode* doubleLeft_right(avlnode*k2){
-
avlnode*k1=k2->left;
-
k2->left=singlerotate_right(k1);
-
return singlerotate_left(k2);
-
}
-
avlnode* doubleright_left(avlnode*k2){
-
avlnode*k1=k2->right;
-
k2->right=singlerotate_left(k1);
-
return singlerotate_right(k2);
-
}
-
avlnode* avlinsert(avlnode*&r,int k){
-
if(r==
NULL){r=
new avlnode();r->key=k;}
-
else{
-
if(r->key>k){
-
r->left=avlinsert(r->left,k);
//类似BST
-
if(get_height(r->left)-get_height(r->right)==
2)
-
{
if(r->left->key>k)r=singlerotate_left(r);
//LL
-
else r=doubleLeft_right(r);
//LR
-
}
//不平衡
-
}
//BST左子树
-
else
if(r->key
-
r->right=avlinsert(r->right,k);
-
if(get_height(r->right)-get_height(r->left)==
2)
-
{
if(r->right->key
//RR
-
else r=doubleright_left(r);
-
}
-
}
//BST右子树
-
else ++(r->freq);
-
}
-
r->height=max1(get_height(r->left),get_height(r->right))+
1;
-
return r;
-
}
-
void avlinsert1(avlnode*&r,int k){
-
if(r==
NULL){r=
new avlnode();r->key=k;}
-
else{
-
if(r->key>k){
-
avlinsert1(r->left,k);
//类似BST
-
-
}
//BST左子树
-
else
if(r->key
-
avlinsert1(r->right,k);
-
-
}
//BST右子树
-
else ++(r->freq);
-
}
-
r->height=max1(get_height(r->left),get_height(r->right))+
1;
-
}
-
void avlcreate(avlnode*&r,int a[],int n){
-
int i;
-
r=
NULL;
-
for(i=
0;i
-
avlinsert(r,a[i]);
-
}
-
int avldelete(avlnode*&root,int k){
-
if(root==
NULL)
return
0;
-
else {
int res;
-
if(k
key){
-
res=avldelete(root->left,k);
-
if(res){
-
if(get_height(root->right)-get_height(root->left)==
2)
-
{
if(root->right->left&&get_height(root->right->left)>get_height(root->right->right))
-
doubleright_left(root);
-
else singlerotate_right(root);
-
}
-
}
-
}
//左子树
-
else
if(k>root->key){
-
res=avldelete(root->right,k);
-
if(res){
-
if(get_height(root->left)-get_height(root->right)==
2)
-
{
if(root->left->right&&get_height(root->left->right)>get_height(root->left->left))
-
doubleLeft_right(root);
-
else singlerotate_left(root);
-
}
-
}
-
}
//右子树
-
else{
-
if(root->left&&root->right){
-
if(get_height(root->left)>get_height(root->right))
-
{avlnode*p1=root;avlnode*p=root->left;
-
while(p->right){p1=p;p=p->right;}
-
//选出左子树最大值
-
root->key=p->key;
-
avldelete(root->left,root->key);
//删除左子树最大值
-
}
-
else {
-
avlnode*p1=root;avlnode*p=root->right;
-
while(p->left){p1=p;p=p->left;}
-
//选出右子树最小值
-
root->key=p->key;
-
avldelete(root->right,root->key);
-
}
//选出右子树最小值
-
}
//左右子树非空,看哪边高
-
//这里也可以采用BST写法不是赋值而是节点取代,只不过麻烦一丢
-
else {
-
avlnode*tmp=root;
-
root=(root->left? root->left:root->right);
-
delete tmp;
-
tmp=
NULL;
-
}
//左右子树有一个不为空
-
}
-
}
-
return
1;
-
}
-
void inorder(avlnode*r){
-
if(r){inorder(r->left);
-
cout<
key<<
" "<height<<
endl;
-
inorder(r->right);
-
}
-
}
-
void avldis(avlnode*r){
-
inorder(r);
cout<<
endl;
-
}
-
void bfs(avlnode*r){
-
if(r==
NULL)
return;
-
avlnode *q[
100];
-
int front=
-1,rear=
-1;
-
rear++;
-
q[rear]=r;
-
while(front
-
front++;
-
avlnode*p=q[front];
-
cout<
key<<
" ";
-
if(p->left){rear++;q[rear]=p->left;}
-
if(p->right){rear++;q[rear]=p->right;}
-
}
-
}
-
void avlbfs(avlnode*r){
-
bfs(r);
-
cout<<
endl;
-
}
-
-
avlnode* avlsearch(avlnode*r,int k){
-
if(r==
NULL)
return
NULL;
-
else
if(k==r->key)
return r;
-
else
if(k
key)
return avlsearch(r->left,k);
-
else
return avlsearch(r->right,k);
-
}
AVL树的测试
首先新建一棵AVL树,然后
依次添加" 3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9 " 到AVL树中;添加完毕之后,再将8 从AVL树中删除。AVL树的添加和删除过程如下图:
(01) 添加3,2
添加3,2都不会破坏AVL树的平衡性。
(02) 添加1
添加1之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
(03) 添加4
添加4不会破坏AVL树的平衡性。
(04) 添加5
添加5之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
(05) 添加6
添加6之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
(06) 添加7
添加7之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
(07) 添加16
添加16不会破坏AVL树的平衡性。
(08) 添加15
添加15之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
(09) 添加14
添加14之后,AVL树失去平衡(RL),此时需要对AVL树进行旋转(RL旋转)。旋转过程如下:
(10) 添加13
添加13之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:
(11) 添加12
添加12之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
(12) 添加11
添加11之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
(13) 添加10
添加10之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
(14) 添加8
添加8不会破坏AVL树的平衡性。
(15) 添加9
但是添加9之后,AVL树失去平衡(LR),此时需要对AVL树进行旋转(LR旋转)。旋转过程如下:
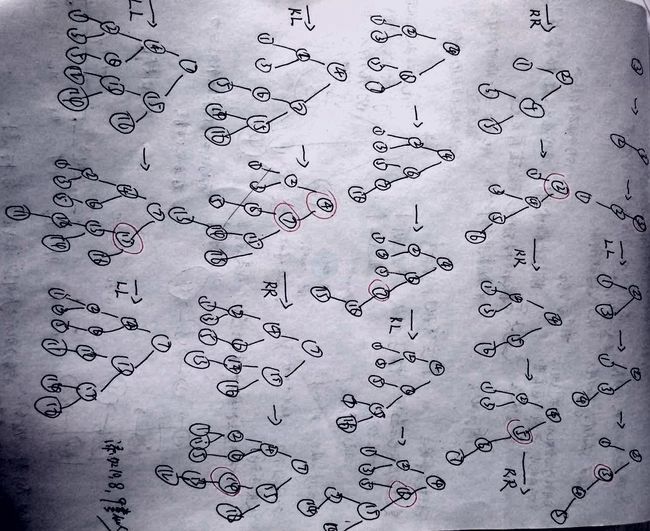
添加完所有数据之后,得到的AVL树如下:
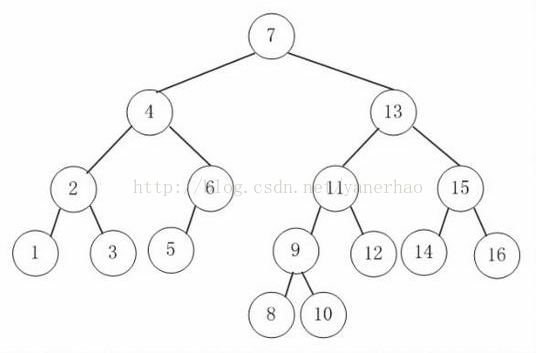
接着,删除节点8.删除节点8并不会造成AVL树的不平衡,所以不需要旋转,操作示意图如下:
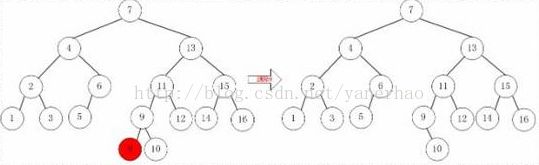
三 红黑树
历史上AVL树流行的另一个版本是红黑树RBT。对红黑树的操作在最坏情况下花费O(log n)时间,而且相对于普通AVL树可能更容易实现。相比较AVL,
1 AVL是严格平衡树,故在增加或者删除节点时,调整所需旋转较多;
2 RBT是平衡与操作复杂性上做了tradeoff,是弱平衡,用非严格的平衡换取增删节点时操作的简单。故当操作主要集中在搜索而非增删时应采用AVL;如果增删操作更多,为了提高可操作性应该选择RBT。其定义:
1 首先是BST,故中序遍历后是非递减序列;
2 弱化的平衡树;
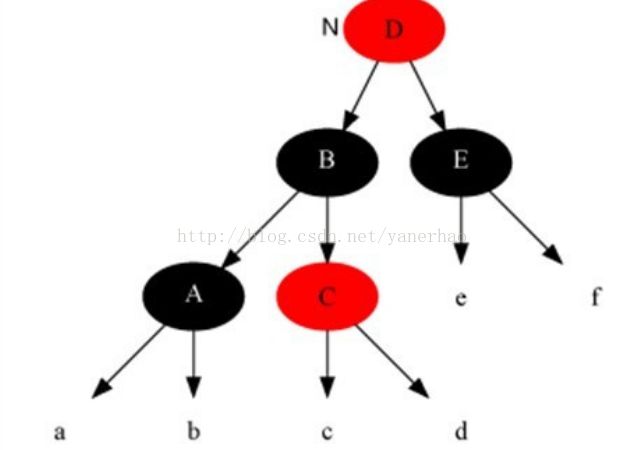
3 不同于BST,AVL,RBT每个节点含有五个域,color/key/left/right/p;
4 根节点一定是黑的(特性2),全空的这种叶子节点也是黑的(特性3),其他每个节点非黑即红(特性1);
5 如果叶子节点是红的,那么两个孩子肯定都是黑的(特性4);
6 对于每一个节点,从该节点到其子孙节点(直到NULL)的所有路径上包含相同数目的黑节点(特性5)
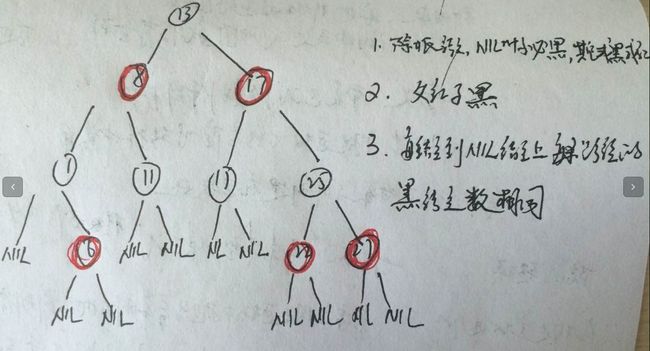
这种着色原则导致RBT高度最多2log(n+1),因此查找肯定是对数操作。通过每条路径上各个节点着色方式的限制,RBT确保没有一条路径会比其他路径长出2倍,因而是一种广泛意义上的平衡。同其他BST一样,问题在于一个新节点的插入,通常做法是将其放在叶子上。如果把它改成黑色,那么肯定违反路径同数目黑色的原则,因此肯定要标为红色:如果它的父节点是黑色,那么插入完成;如果父节点是红色,那么违反父红子黑原则,故需要调整。主要是颜色的改变和旋转。
我们在对红黑树进行插入和删除等操作时,对树做了修改,那么可能会违背红黑树的性质。为了保持红黑树的性质,我们可以通过对树进行旋转,即修改树种某些结点的颜色及指针结构,以达到对红黑树进行插入、删除结点等操作时,红黑树依然能保持它特有的性质.
RBT的旋转:
1 左旋(逆时针旋转)
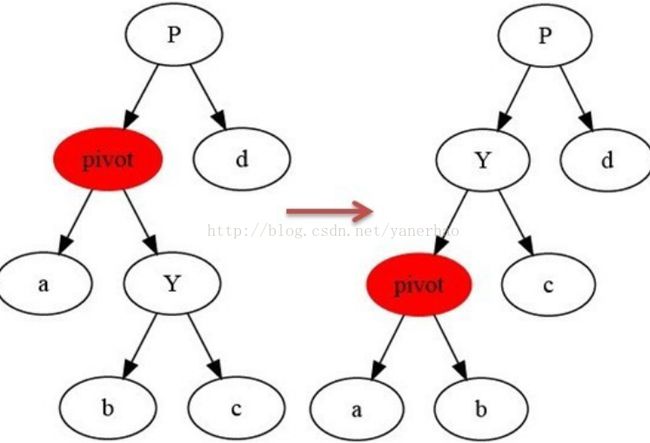
可以看到类似AVL里的LL型调整,也是逆时针旋转
2 右旋(顺时针旋转)
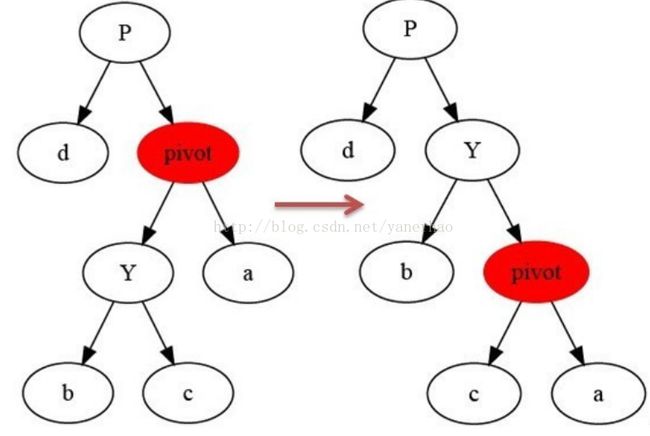
可以看到类似AVL树里的RR型调整即顺时针旋转。
但是旋转只能保持作为平衡树的性质,而RBT红黑性不能保持,故还需要颜色重涂来保证。总结来看就是两条:1 部分结点颜色,重新着色;2 调整部分指针的指向,即左旋、右旋。
下面将通过图和代码来阐述复杂的插入和删除:
1 RBT的插入
向一棵含有n个结点的红黑树插入一个新结点的操作可以在O(lgn)时间内完成。
插入前:选择的插入节点是红色,按照BST准则找到合适位置;
插入时:
情况1 插入的就是根节点
原树是空树,插入红节点,违背根黑;
对策:需要把节点涂成黑色;
-
void insert_case1(node *n){
-
if(n->parent==
NULL)
-
n->color=BLACK;
//就是根节点没有父节点
-
else
-
insert_case2(n);
-
}
情况2 插入的节点的父节点是黑色
成功插入
-
void insert_case2(node *n){
-
if(n->parent&&n->parent->color==BLACK)
-
return;
-
else insert_case3(n);
-
}
情况3 插入的节点的父节点是红色且叔叔节点是红色
此时祖父节点一定存在,与此同时,又分为父结点是祖父结点的左子还是右子,对于对称性,我们只要解开一个方向就可以,在此,我们只考虑父结点为祖父左子的情况。
对策:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
“当前节点”和“父节点”都是红色,违背“特性(4)”。所以,将“父节点”设置“黑色”以解决这个问题。但是,将“父节点”由“红色”变成“黑色”之后,违背了“特性(5)”:因为,包含“父节点”的分支的黑色节点的总数增加了1。 解决这个问题的办法是:将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”。关于这里,说明几点:第一,为什么“祖父节点”之前是黑色?这个应该很容易想明白,因为在变换操作之前,该树是红黑树,“父节点”是红色,那么“祖父节点”一定是黑色。 第二,为什么将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”;能解决“包含‘父节点’的分支的黑色节点的总数增加了1”的问题。这个道理也很简单。“包含‘父节点’的分支的黑色节点的总数增加了1” 同时也意味着 “包含‘祖父节点’的分支的黑色节点的总数增加了1”,既然这样,我们通过将“祖父节点”由“黑色”变成“红色”以解决“包含‘祖父节点’的分支的黑色节点的总数增加了1”的问题; 但是,这样处理之后又会引起另一个问题“包含‘叔叔’节点的分支的黑色节点的总数减少了1”,现在我们已知“叔叔节点”是“红色”,将“叔叔节点”设为“黑色”就能解决这个问题。 所以,将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”;就解决了该问题。按照上面的步骤处理之后:当前节点、父节点、叔叔节点之间都不会违背红黑树特性,但祖父节点却不一定。若此时,祖父节点是根节点,直接将祖父节点设为“黑色”,那就完全解决这个问题了;若祖父节点不是根节点,那我们需要将“祖父节点”设为“新的当前节点”,接着对“新的当前节点”进行分析。
-
void insert_case3(node *n){
-
if(uncle(n)&&uncle(n)->color==RED)
-
{ n->parent->color=BLACK;
-
uncle(n)=BLACK;
-
grnadpa(n)->color=RED;
-
insert_case1(grandpa(n));}
//把祖父节点当作新节点重新开始
-
else
-
insert_case4(n);
//否则叔叔是黑色节点
-
}
插入4节点变化前后:
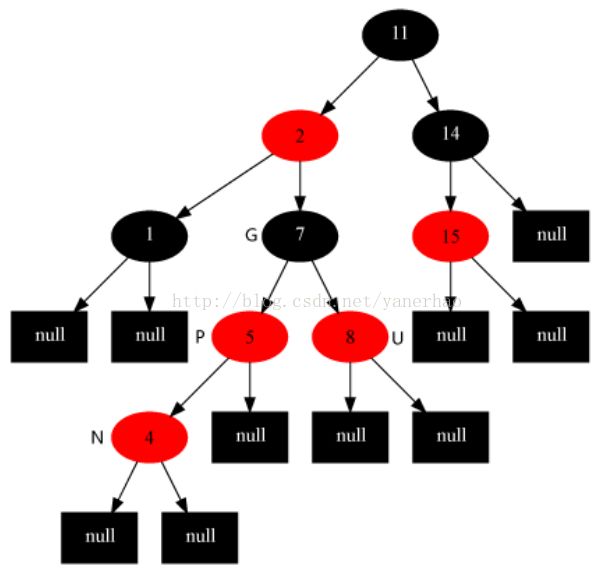
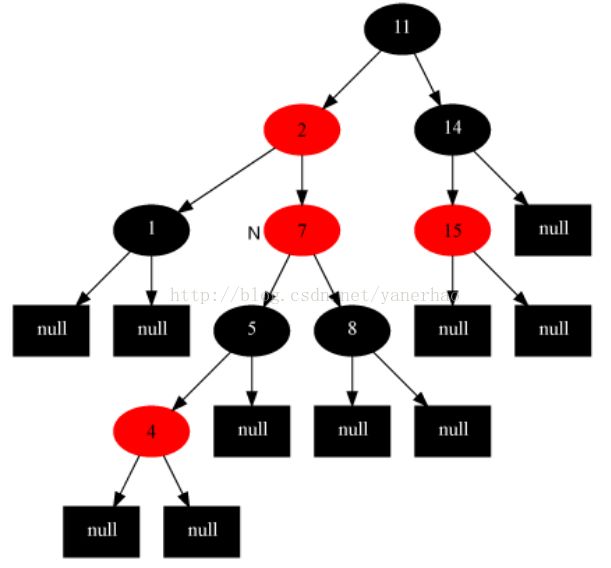
情况4 插入的节点的父节点是红色且叔叔节点是黑色或者空NIL,当前节点是父节点右子(父节点仍然是祖父的左孩子)
对策:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
首先,将“父节点”作为“新的当前节点”;接着,以“新的当前节点”为支点进行左旋。 为了便于理解,我们先说明第(02)步,再说明第(01)步;为了便于说明,我们设置“父节点”的代号为F(Father),“当前节点”的代号为S(Son)。为什么要“以F为支点进行左旋”呢?根据已知条件可知:S是F的右孩子。而之前我们说过,我们处理红黑树的核心思想:将红色的节点移到根节点;然后,将根节点设为黑色。既然是“将红色的节点移到根节点”,那就是说要不断的将破坏红黑树特性的红色节点上移(即向根方向移动)。 而S又是一个右孩子,因此,我们可以通过“左旋”来将S上移!按照上面的步骤(以F为支点进行左旋)处理之后:若S变成了根节点,那么直接将其设为“黑色”,就完全解决问题了;若S不是根节点,那我们需要执行步骤(01),即“将F设为‘新的当前节点’”。那为什么不继续以S为新的当前节点继续处理,而需要以F为新的当前节点来进行处理呢?这是因为“左旋”之后,F变成了S的“子节点”,即S变成了F的父节点;而我们处理问题的时候,需要从下至上(由叶到根)方向进行处理;也就是说,必须先解决“孩子”的问题,再解决“父亲”的问题;所以,我们执行步骤(01):将“父节点”作为“新的当前节点”。
-
void insert_case4(node *n){
-
if(n==n->parent->right&&n->parent==grandpa(n)->left)
-
{ rotate_left(n->parent);
-
n=n->left;
//作为新节点
-
}
-
else
if(n==n->parent->left&&n->parent==grandpa(n)->right)
-
{ rotate_right(n->parent);
-
n=n->right;
//作为新节点
-
}
-
insert_case5(n);
-
}
接着上图,7看成新插入的节点:
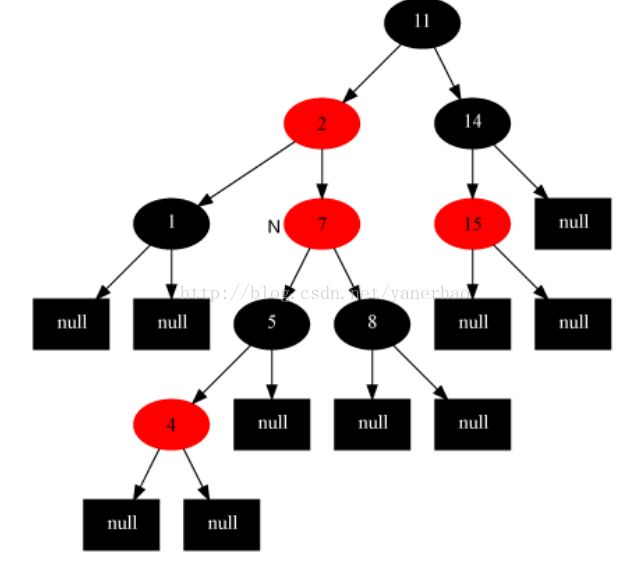
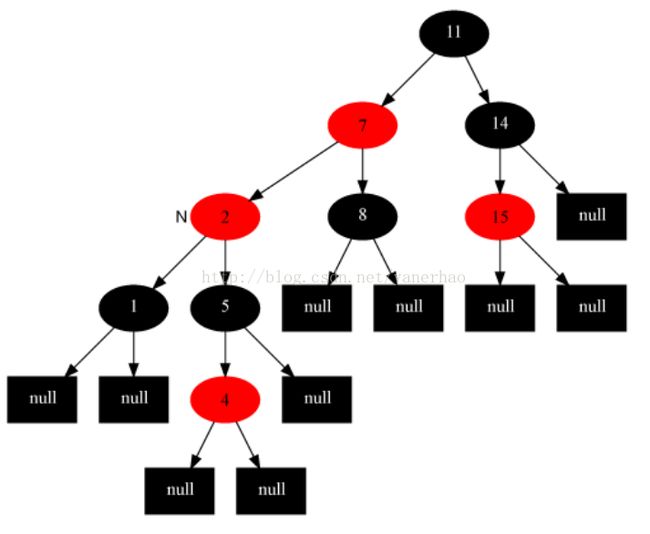
情况5 当前节点的父节点是红,叔叔是黑或者空NIL,当前节点是父节点的左子(父节点又是祖父的左孩子)
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“叔叔节点”为U(Uncle),“父节点”为F(Father),祖父节点为G(Grand-Father)。S和F都是红色,违背了红黑树的“特性(4)”,我们可以将F由“红色”变为“黑色”,就解决了“违背‘特性(4)’”的问题;但却引起了其它问题:违背特性(5),因为将F由红色改为黑色之后,所有经过F的分支的黑色节点的个数增加了1。那我们如何解决“所有经过F的分支的黑色节点的个数增加了1”的问题呢? 我们可以通过“将G由黑色变成红色”,同时“以G为支点进行右旋”来解决。
-
void insert_case5(node *n){
-
n->parent->color=BLACK;
-
grandpa(n)->color=RED;
-
if(n==n->parent->left&&n->parent==grandpa(n)->left)
-
rotate_right(grandpa(n));
//顺时针
-
else
-
rotate_left(grandpa(n));/n 是其父节点的右孩子,而父节点P又是其父G的右孩子
-
}
接着上图,相当于新节点为2
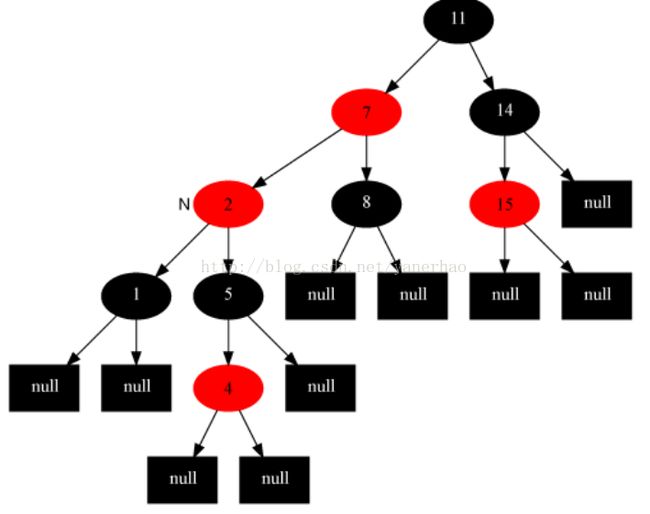
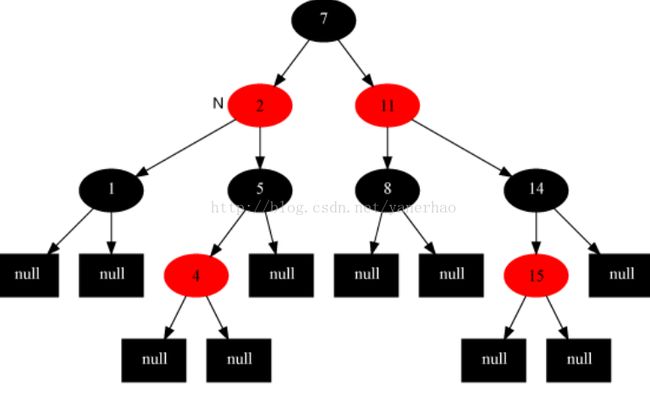
2 RBT的删除
下面所有的文字,则是针对红黑树删除结点后,所做的修复红黑树性质的工作:
前面我们将"删除红黑树中的节点"大致分为两步,在第一步中"将红黑树当作一颗二叉查找树,将节点删除"后,可能违反"特性(2)、(4)、(5)"三个特性。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。为了便于分析,我们假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。为什么呢?通过删除算法,我们知道:删除节点y之后,x占据了原来节点y的位置。 既然删除y(y是黑色),意味着减少一个黑色节点;那么,再在该位置上增加一个黑色即可。这样,当我们假设"x包含一个额外的黑色",就正好弥补了"删除y所丢失的黑色节点",也就不会违反"特性(5)"。 因此,假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。现在,x不仅包含它原本的颜色属性,x还包含一个额外的黑色。即x的颜色属性是"红+黑"或"黑+黑",它违反了"特性(1)"。现在,我们面临的问题,由解决"违反了特性(2)、(4)、(5)三个特性"转换成了"解决违反特性(1)、(2)、(4)三个特性"。RB-DELETE-FIXUP需要做的就是通过算法恢复红黑树的特性(1)、(2)、(4)。删除后修正的思想是:将x所包含的额外的黑色不断沿树上移(向根方向移动),直到出现下面的姿态:a) x指向一个"红+黑"节点。此时,将x设为一个"黑"节点即可。b) x指向根。此时,将x设为一个"黑"节点即可。c) 非前面两种姿态。
情况1:当前节点是红色:
解法,直接把当前节点染成黑色,结束。此时红黑树性质全部恢复。
情况2: 当前节点是黑色但也是根节点
-
void delete_case2(node*n){
-
if(n->color==BLACK&&n->parent==
NULL)
-
return;
-
delete_case3(n);
-
}
解法:删除成功,结束
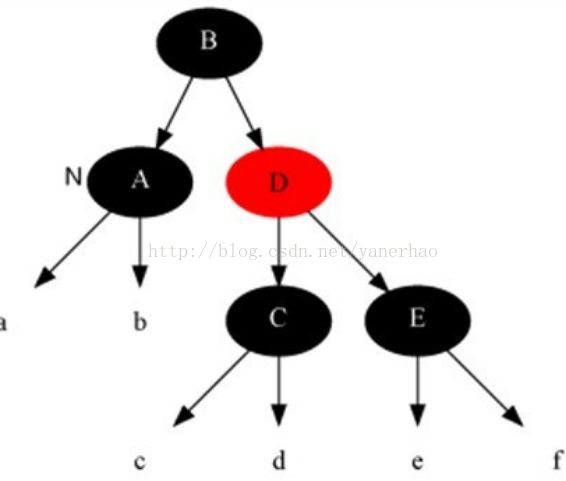
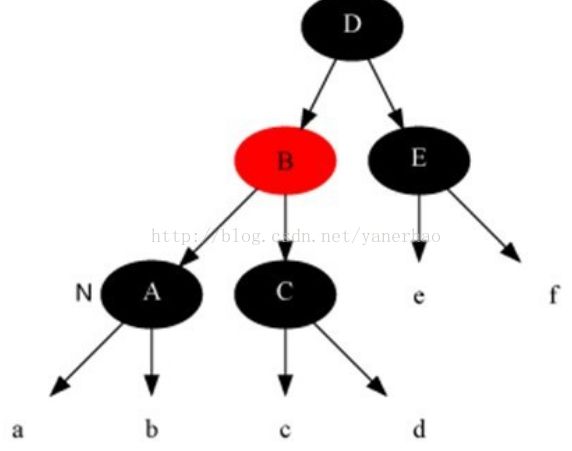
情况3: 当前节点x是黑色且兄弟节点w是红色(则(此时父节点和兄弟节点的子节点分为黑))
解法:把父节点染成红色,把兄弟结点染成黑色,之后重新进入算法(我们只讨论当前节点是其父节点左孩子时的情况)。然后,针对父节点做一次左旋。此变换后把问题转化为兄弟节点为黑色的情况。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
这样做的目的是将“Case 3”转换为“Case 4”、“Case 5”或“Case 6”,从而进行进一步的处理。对x的父节点进行左旋;左旋后,为了保持红黑树特性,就需要在左旋前“将x的兄弟节点设为黑色”,同时“将x的父节点设为红色”;左旋后,由于x的兄弟节点发生了变化,需要更新x的兄弟节点,从而进行后续处理。
-
void delete_case3(node *n){
-
if(w->color==RED)
-
{
-
w->color=BLACK;
-
n->parent->color=RED;
-
rotate_left(n->parent);
//左旋
-
}
-
else
-
delete_case4(n);
-
}
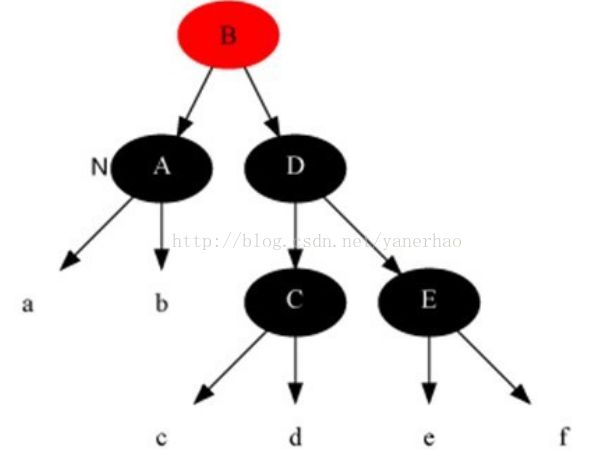
情况4:当前节点是黑色,
解法:把当前节点和兄弟节点中抽取一重黑色追加到父节点上,把父节点当成新的当前节点,重新进入算法。
-
void delete_case4(node *n){
-
if(w->left->color==BLACK&&w->right->color==BLACK){
-
w->color=RED;
-
n=n->parent;
//父节点作为新节点
-
}
-
else delete_case1(n);
//重新进入算法
-
}
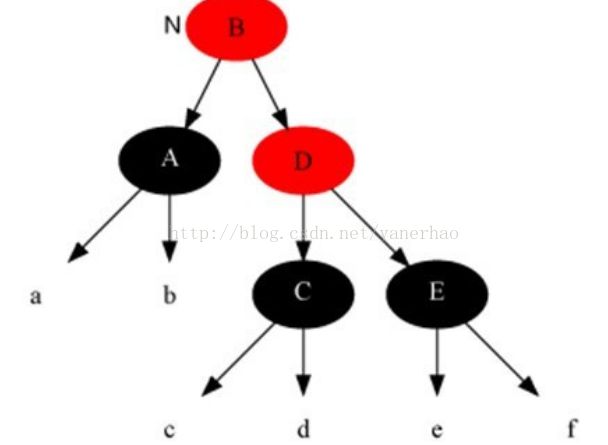
情况5:当前节点颜色是黑色,兄弟节点是黑色,兄弟的左子是红色,右子是黑色。
解法:把兄弟结点染红,兄弟左子节点染黑,之后再在兄弟节点为支点解右旋,之后重新进入算法。此是把当前的情况转化为情况6,而性质得以保持。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
我们处理“Case 3”的目的是为了将“Case 5”进行转换,转换成“Case 6”,从而进行进一步的处理。转换的方式是对x的兄弟节点进行右旋;为了保证右旋后,它仍然是红黑树,就需要在右旋前“将x的兄弟节点的左孩子设为黑色”,同时“将x的兄弟节点设为红色”;右旋后,由于x的兄弟节点发生了变化,需要更新x的兄弟节点,从而进行后续处理。
-
void delete_case5(node*n){
-
if(w->left->color==RED&&w->right->color==BLACK){
-
w->left->color=BLACK;
-
w->color=RED;
-
rotate_right(w);
-
w=n->parent->right; }
-
else
-
delete_case6(n);
-
}
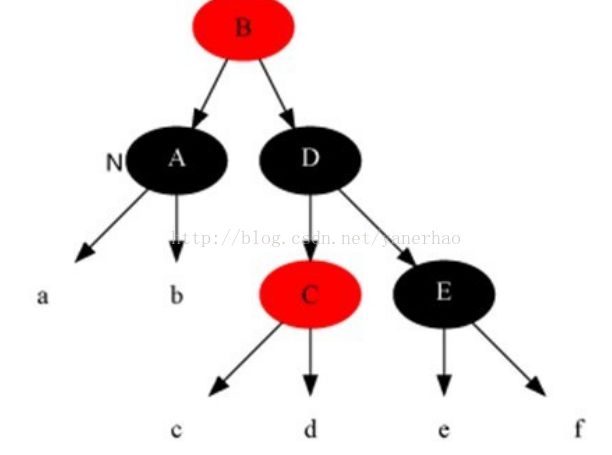
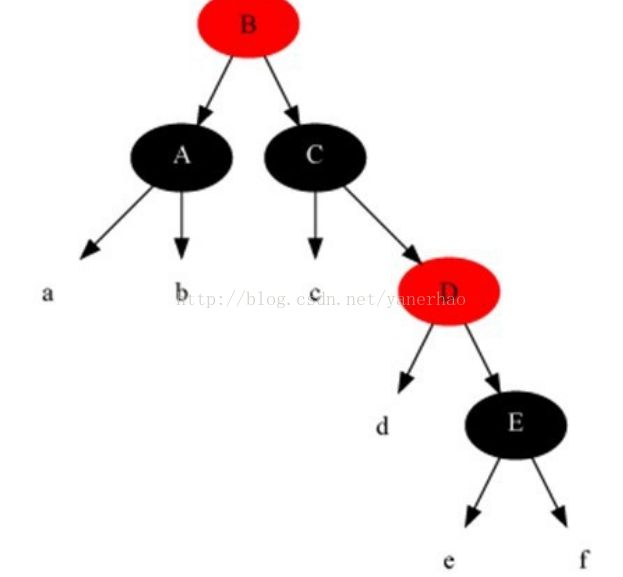
情况6:当前节点颜色是黑色,它的兄弟节点是黑色,但是兄弟节点的右子是红色,兄弟节点左子的颜色任意。
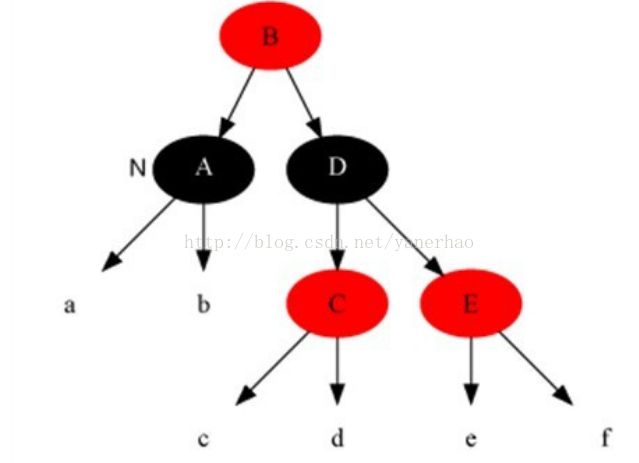
解法:把兄弟节点染成当前节点父节点的颜色,把当前节点父节点染成黑色,兄弟节点右子染成黑色,之后以当前节点的父节点为支点进行左旋,此时算法结束,红黑树所有性质调整正确。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
我们处理“Case 6”的目的是:去掉x中额外的黑色,将x变成单独的黑色。处理的方式是“:进行颜色修改,然后对x的父节点进行左旋。下面,我们来分析是如何实现的。为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“兄弟节点的左孩子”为BLS(Brother's Left Son),“兄弟节点的右孩子”为BRS(Brother's Right Son),“父节点”为F(Father)。我们要对F进行左旋。但在左旋前,我们需要调换F和B的颜色,并设置BRS为黑色。为什么需要这里处理呢?因为左旋后,F和BLS是父子关系,而我们已知BL是红色,如果F是红色,则违背了“特性(4)”;为了解决这一问题,我们将“F设置为黑色”。 但是,F设置为黑色之后,为了保证满足“特性(5)”,即为了保证左旋之后:第一,“同时经过根节点和S的分支的黑色节点个数不变”。若满足“第一”,只需要S丢弃它多余的颜色即可。因为S的颜色是“黑+黑”,而左旋后“同时经过根节点和S的分支的黑色节点个数”增加了1;现在,只需将S由“黑+黑”变成单独的“黑”节点,即可满足“第一”。第二,“同时经过根节点和BLS的分支的黑色节点数不变”。若满足“第二”,只需要将“F的原始颜色”赋值给B即可。之前,我们已经将“F设置为黑色”(即,将B的颜色"黑色",赋值给了F)。至此,我们算是调换了F和B的颜色。第三,“同时经过根节点和BRS的分支的黑色节点数不变”。在“第二”已经满足的情况下,若要满足“第三”,只需要将BRS设置为“黑色”即可。经过,上面的处理之后。红黑树的特性全部得到的满足!接着,我们将x设为根节点,就可以跳出while循环(参考伪代码);即完成了全部处理。至此,我们就完成了Case 6的处理。理解Case 4的核心,是了解如何“去掉当前节点额外的黑色”。
-
void delete_case6(node *n){
-
w->color=n->parent->color;
-
n->parent->color=BLACK;
-
w->right->color=BLACK;
-
rotate_left(n->parent);
-
}
红黑树的插入、删除情况时间复杂度的分析
因为每一个红黑树也是一个特化的二叉查找树,因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而,在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次。
四 B-/B+树
由于篇幅有限,再加上B树独有特征,B树相关知识在下一篇介绍。
具体参考:
http://www.cnblogs.com/skywang12345/p/3245399.html#a34