三角函数和反三角函数图像、导数、积分、等式关系

之前对三角函数的理解仅局限于sin，cos，tan。但是目前遇到的都是些csc，sec，cot，arctan，arccos，arcsin。积分和求导还有一堆公式
最近看到了一个六边形记忆法，更加简便。

1.倒三角：
sin²+cos²=1
tan²+1=sec²
1+cot²=csc²
2.对角线倒数
3.临点积
tan*cos=sin
sin*cot=cos
4.求导:左三角导数正，右三角导数负
上互换：
sin'=cos
cos'=-sin
中下2：
tan'=sec²
cot'=-csc²
下中下：
sec'=tan*sec
csc=-cot*csc
5.求积分：
sec积分：ln|sec+tan|+C
csc积分：-ln|csc+cot|+C

1.三角函数及其倒数

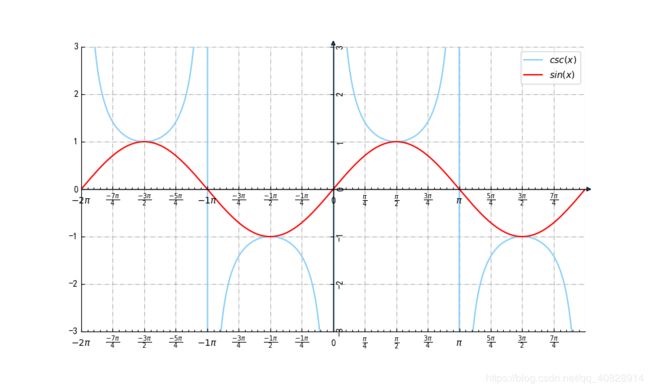
sin(x)和csc(x)

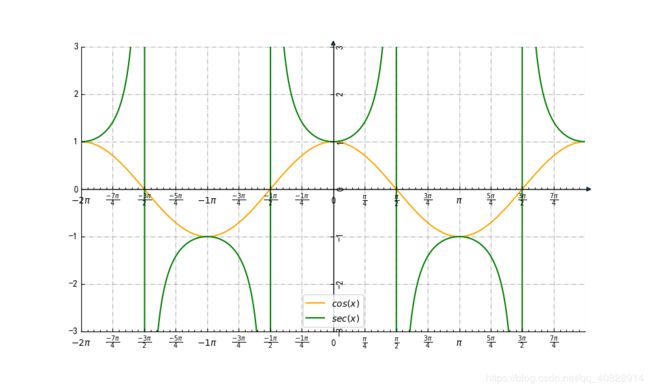
cos(x)和sec(x)

tan(x)和cot(x)

分析其特点：

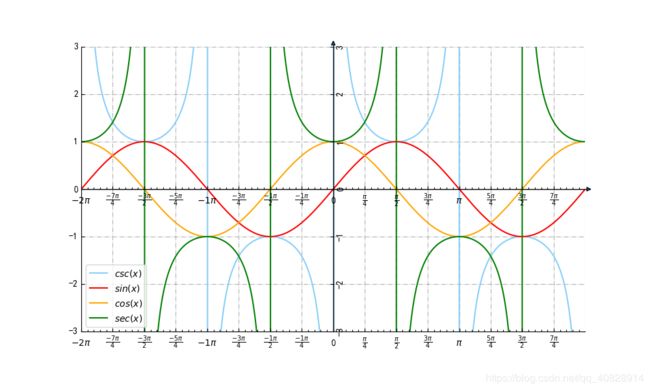
这几个三角函数两两之间是倒数的关系。
他们共同特点：
1.在同一点处他们函数值相乘为1
他们有共同交点在y=1和y=-1这两条直线上
2.在同一区间他们同号。
其中一个函数->0+，那么另一个函数->+无穷
其中一个函数->0-，那么另一个函数->-无穷
3.在y=1和y=-1处对应的x坐标记为a。
在a的左右邻域他们增减性相反

2.三角函数及其反函数

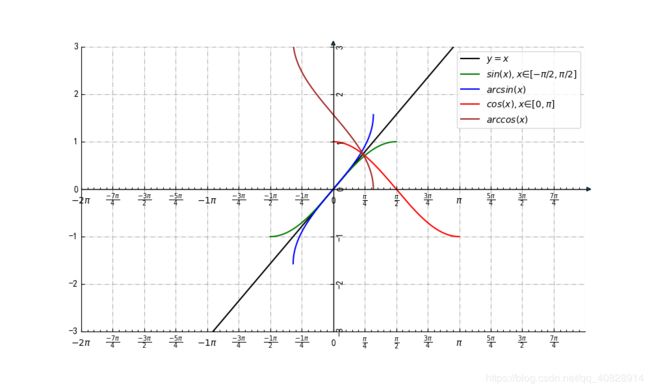
sin(x)和arcsin(x）

注：
正弦函数y=sinx，x∈R因为在整个定义域上没有一一对应关系，所以不存在反函数。
反正弦函数对这样一个函数y=sinx，x∈[-π/2，π/2]成立，这里截取的是正弦函数靠近原点的一个单调区间。y=arcsinx 的定义域：[-1,1],值域：[-π/2,π/2]

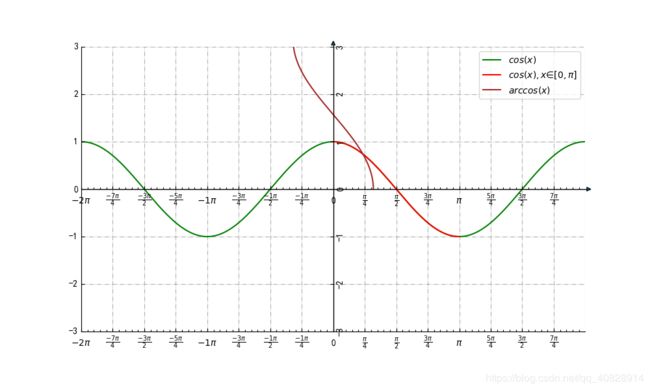
cos(x)和arccos(x)

y=cosx，x∈R因为在整个定义域上没有一一对应关系，所以不存在反函数。
arccos(x)对这样一个函数y=cosx，x∈[0，π]成立，这里截取的是余弦函数靠近原点的一个单调区间，arccosx 值域是 :[0,π],定义域[-1,1]。

tan(x)和arctan(x)

注：
由于正切函数y=tanx在定义域R上不具有一一对应的关系，所以不存在反函数。

选取正切函数的一个单调区间。而由于正切函数在开区间(-π/2,π/2)中是单调连续的，因此，反正切函数是存在且唯一确定的。arctanx的值域是：(-π/2,π/2)。

分析其特点

他们的特点其实就是原函数和反函数的特点，
关于y=x对称。函数与其反函数在其对应区间内单调性相同。

3.python画图源代码

画图及坐标配置请参考matplotlib官方网站：https://matplotlib.org/gallery/index.html

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号

#import pandas as pd
import numpy as np
from mpl_toolkits.axisartist.axislines import SubplotZero
import numpy as np
from matplotlib.ticker import MultipleLocator, FuncFormatter

fig = plt.figure(1, (10, 6))

ax = SubplotZero(fig, 1, 1, 1)
fig.add_subplot(ax)

"""新建坐标轴"""
ax.axis["xzero"].set_visible(True)
#ax.axis["xzero"].label.set_text("新建y=0坐标")
#ax.axis["xzero"].label.set_color('green')
ax.axis['yzero'].set_visible(True)
# ax.axis["yzero"].label.set_text("新建x=0坐标")

# 新建一条y=2横坐标轴
#ax.axis["新建1"] = ax.new_floating_axis(nth_coord=0, value=1,axis_direction="bottom")
#ax.axis["新建1"].toggle(all=True)
#ax.axis["新建1"].label.set_text("y = 1横坐标")
#ax.axis["新建1"].label.set_color('blue')

"""坐标箭头"""
ax.axis["xzero"].set_axisline_style("-|>")
ax.axis["yzero"].set_axisline_style("-|>")


"""隐藏坐标轴"""
# 方法一：隐藏上边及右边
# ax.axis["right"].set_visible(False)
# ax.axis["top"].set_visible(False)
#方法二：可以一起写
ax.axis["top",'right'].set_visible(False)
# 方法三：利用 for in
# for n in ["bottom", "top", "right"]:
#  ax.axis[n].set_visible(False)




x = np.arange(-2*np.pi, 2*np.pi, 0.01)
def pi_formatter(x, pos):
    """ 
    将数值转换为以pi/4为单位的刻度文本 
    """
    m = np.round(x / (np.pi / 4))
    n = 4
    if m % 2 == 0: m, n = m / 2, n / 2
    if m % 2 == 0: m, n = m / 2, n / 2
    if m == 0:
        return "0"
    if m == 1 and n == 1:
        return "$\pi$"
    if n == 1:
        return r"$%d \pi$" % m
    if m == 1:
        return r"$\frac{\pi}{%d}$" % n
    return r"$\frac{%d \pi}{%d}$" % (m, n)


# 设置两个坐标轴的范围
plt.ylim(-3 , 3)
plt.xlim(-2*np.pi, np.max(x))

# 设置图的底边距
plt.subplots_adjust(bottom=0.15)

plt.grid()  # 开启网格

# 主刻度为pi/4
ax.xaxis.set_major_locator(MultipleLocator(np.pi / 4))

# 主刻度文本用pi_formatter函数计算
ax.xaxis.set_major_formatter(FuncFormatter(pi_formatter))

# 副刻度为pi/20
ax.xaxis.set_minor_locator(MultipleLocator(np.pi / 20))

# 设置刻度文本的大小
for tick in ax.xaxis.get_major_ticks():
    tick.label1.set_fontsize(16)

"""设置刻度
ax.set_ylim(-3, 3)
ax.set_yticks([-1,-0.5,0,0.5,1])
ax.set_xlim([-5, 8])
"""

# ax.set_xticks([-5,5,1])

#设置网格样式
ax.grid(True, linestyle='-.')

'''

ax.plot(x, 1/np.sin(x),color='lightskyblue', label="$csc(x)$")
ax.plot(x, np.sin(x),color='red', label="$sin(x)$")

ax.plot(x, np.cos(x),color='orange', label="$cos(x)$")
ax.plot(x, 1/np.cos(x),color='green', label="$sec(x)$")


ax.plot(x, np.sin(x)/np.cos(x),color='orange', label="$tan(x)$")
ax.plot(x, np.cos(x)/np.sin(x),color='skyblue', label="$cot(x)$")

'''


ax.plot(x, x,color='black', label="$y=x$")

x3 = np.arange(-np.pi/2, np.pi/2, 0.01)
ax.plot(x, np.sin(x),color='red', label="$sin(x)$")
ax.plot(x3, np.sin(x3),color='green', label="$sin(x),x∈[-π/2,π/2]$")
ax.plot(np.sin(x3), x3 ,color='blue', label="$arcsin(x)$")

x2 = np.arange(0, np.pi, 0.01)
ax.plot(x, np.cos(x),color='green', label="$cos(x)$")
ax.plot(x2, np.cos(x2),color='red', label="$cos(x),x∈[0,π]$")
ax.plot(np.cos(x2), x2 ,color='brown', label="$arccos(x)$")
'''
x4=np.arange(-np.pi/2, np.pi/2, 0.01)
ax.plot(x, np.tan(x),color='red', label="$tan(x)$")
ax.plot(x4, np.tan(x4),color='green', label="$tan(x),x∈(-π/2,π/2)$")
ax.plot(np.tan(x4), x4 ,color='blue', label="$arctan(x)$")
'''
plt.legend()
plt.show()
# 存为图像
# fig.savefig('test.png')