支持向量机算法与实现
文章目录
- 1 算法思想
- 2 算法步骤
- 2.1 线性可分支持向量机
- 2.2 SVM的二次凸函数和约束条件
- 2.3 非线性类问题——核技巧(kernel trick)
- 3 算法实现
1 算法思想
支持向量机(support vector machines) 是找到一个超平面(hyperplane)将数据划分为一类与其他类的一种二类分类模型,分离间隔最大而区别于感知机。
适用于:
- 数据可直接分为两类(采用error-correcting output codes 方法区分多类);
- 高维不能线性可分的数据;
- 简单分类。
支持向量机类别:
- 线性可分支持向量机(linear support vector machine in linearly separable case)——硬间隔最大化(hard margin maximization)
- 线性支持向量机(linear support vector machine)——软间隔最大化(soft margin maximization)
- 非线性支持向量机(non-linear support vector machine)——核技巧(kernel trick)
2 算法步骤
2.1 线性可分支持向量机
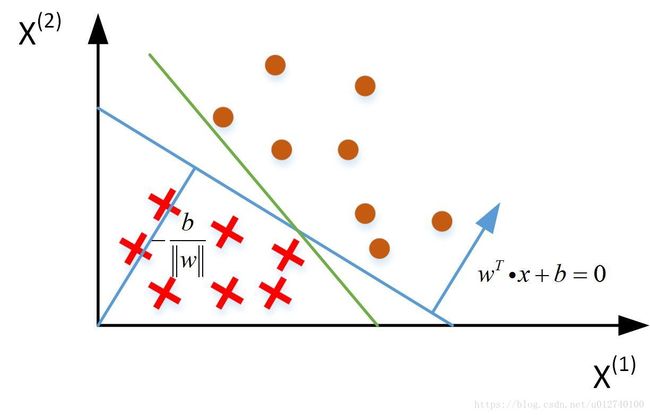
由线性分类器可知:一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为:
w T x + b = 0 w^Tx+b=0 wTx+b=0
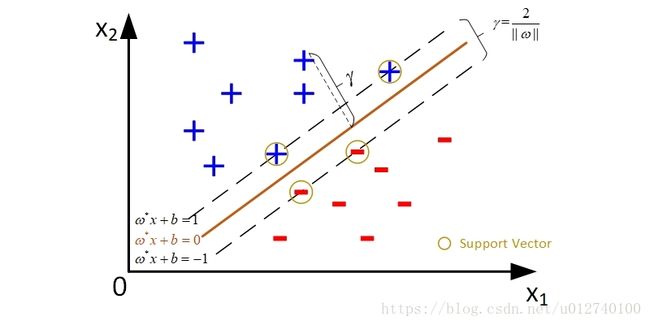
分离超平面: w ∗ ⋅ x + b ∗ = 0 w^*\cdot x+b^*=0 w∗⋅x+b∗=0
分类决策函数:
f ( x ) = s i g n ( w ∗ ⋅ x + b ∗ ) = > { H 1 : w 0 + w 1 x 1 + w 2 x 2 ≥ 1 for y i = + 1 , H 2 : w 0 + w 1 x 1 + w 2 x 2 ≤ 1 for y i = − 1. = > y i ( w 0 + w 1 x 1 + w 2 x 2 ) ≥ 1 f(x)=\mathrm{sign}(w^*\cdot x+b^*) => \left\{ \begin{array}{rl} H_1: w_0+w_1x_1+w_2x_2 \geq 1 & \text{for } y_i=+1,\\ H_2: w_0+w_1x_1+w_2x_2 \leq 1 & \text{for } y_i=-1.\\ \end{array} \right.\\ \qquad =>y_i(w_0+w_1x_1+w_2x_2) \geq 1 f(x)=sign(w∗⋅x+b∗)=>{H1:w0+w1x1+w2x2≥1H2:w0+w1x1+w2x2≤1for yi=+1,for yi=−1.=>yi(w0+w1x1+w2x2)≥1
函数间隔(functional margin): γ ^ = min i = 1 , . . . , N γ ^ i \hat{\gamma}=\min \limits_{i=1,...,N} \hat{\gamma}_i γ^=i=1,...,Nminγ^i
对于样本点 ( x i , y i ) (x_i,y_i) (xi,yi) , γ ^ i = y i ( w ⋅ x i + b ) \hat{\gamma}_i=y_i(w \cdot x_i+b ) γ^i=yi(w⋅xi+b)。
几何间隔(geometric margin): γ = min i = 1 , . . . , N γ i = γ ^ ∥ w ∥ \gamma=\min \limits_{i=1,...,N}\gamma_i=\frac{\hat{\gamma}}{\parallel w \parallel} γ=i=1,...,Nminγi=∥w∥γ^
对于样本点 ( x i , y i ) (x_i,y_i) (xi,yi) , γ i = y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) = γ ^ i ∥ w ∥ \gamma_i=y_i(\frac{w}{\parallel w \parallel} \cdot x_i+ \frac{b}{\parallel w \parallel})=\frac{\hat{\gamma}_i}{\parallel w \parallel} γi=yi(∥w∥w⋅xi+∥w∥b)=∥w∥γ^i
支持向量:
欲找到具有最大间隔的划分超平面,也就是是 γ \gamma γ 最大,即:
max w , b 2 ∥ w ∥ s . t . y i ( w T ⋅ x i + b ) ≥ 1 , i = 1 , 2 , . . . , m . \max \limits_{w,b} \ \ \frac{2}{\parallel w \parallel} \\ s.t. \ \ y_i(w^T \cdot x_i+b) \ge 1, \ i=1,2,...,m. w,bmax ∥w∥2s.t. yi(wT⋅xi+b)≥1, i=1,2,...,m.
最大间隔分类器就是我们求取的分类超平面, 等于 max ( 最 大 间 隔 ) \max(最大间隔) max(最大间隔), 而函数间隔假设为1,就可得到最大间隔超平面: max 1 ∥ w ∥ \max \frac{1}{\parallel w \parallel} max∥w∥1, 而约束条件是因为函数间隔是所有样本点的间隔函数中最小值。
2.2 SVM的二次凸函数和约束条件
支持向量机的学习策略是间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming).
仅需最大化 ∥ w ∥ − 1 \parallel w \parallel^{-1} ∥w∥−1,这等价于最小化 ∥ w ∥ 2 \parallel w \parallel^{2} ∥w∥2。于是,上式可重写为:
(1) min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T ⋅ x i + b ) ≥ 1 , i = 1 , 2 , . . . , m . \min \limits_{w,b} \ \ \frac{1}{2}\parallel w \parallel^2 \qquad s.t. \ \ y_i(w^T \cdot x_i+b) \ge 1, \ i=1,2,...,m. \tag{1} w,bmin 21∥w∥2s.t. yi(wT⋅xi+b)≥1, i=1,2,...,m.(1)
这是支持向量机的基本型,其本身为一个凸二次规划问题。
使用拉格朗日乘子法可得到其“对偶问题”(dual problem),其拉格朗日函数可写为:
(2) L ( ω , b , α ) = 1 2 ∥ ω ∥ 2 + ∑ i = 1 m α i ( 1 − y i ( ω T x i + b ) ) L(\omega ,b, \alpha )=\frac{1}{2}\left \| \omega \right \|^2+\sum \limits_{i=1}^m \alpha _i(1-y_i(\omega ^T x_i+b)) \tag{2} L(ω,b,α)=21∥ω∥2+i=1∑mαi(1−yi(ωTxi+b))(2)
其中 α i \alpha_i αi是拉格朗日乘子。
利用对偶性的结论, 对 L ( ω , b , α ) L(\omega,b,\alpha) L(ω,b,α)关于 ω \omega ω和 b b b求偏导数:
(3) ∂ L ∂ ω = 0 ⇒ ω = ∑ i = 1 n α i x i y i ∂ L ∂ b = 0 ⇒ ∑ i = 1 n α i y i = 0 \frac{\partial L}{\partial \omega}=0 \Rightarrow \omega = \sum \limits_{i=1}^n \alpha _i x_i y_i \\ \frac{\partial L}{\partial b}=0 \Rightarrow \sum \limits_{i=1}^n \alpha _i y_i = 0 \tag{3} ∂ω∂L=0⇒ω=i=1∑nαixiyi∂b∂L=0⇒i=1∑nαiyi=0(3)
将上式带入式(2)中,可得式(1)的对偶问题:
(4) max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 , i = 1 , 2 , . . . , m \max \limits_{\alpha }\sum \limits_{i=1}^m \alpha _i - \frac{1}{2}\sum \limits_{i=1}^m \sum \limits_{j=1}^m \alpha _i\alpha _j y_i y_j x_i^T x_j \\ s.t. \ \sum \limits_{i=1}^m \alpha _i y_i=0, \ \alpha _i \ge 0, i=1,2,...,m \tag{4} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t. i=1∑mαiyi=0, αi≥0,i=1,2,...,m(4)
实际任务中,求解式(4)会造成很大的开销,**SMO(Sequential Minimal Optimization)**是一种求解的高效算法。
SMO 算法是支持向量机学习的一种快速算法,其特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题,并对子问题进行解析求解,直到所有变量满足 KKT 条件为止。
SMO的基本思路类似动态规划, 也是一种启发式算法,它将原优化问题分解为多个小优化问题来求解,并且对这些小优化问题进行顺序求解得到的结果作为作为整体的结果。
解出 α \alpha α 后,求出 ω \omega ω 与 b b b 即可得到模型
f ( x ) = ω T x + b = ∑ i = 1 m α i y i x i T x + b f(x) = \omega ^T x+b = \sum \limits_{i=1}^m \alpha _i y_i x_i^Tx+b f(x)=ωTx+b=i=1∑mαiyixiTx+b
因式(1)中有不等式约束,上述过程需满足KKT(Karush-Kuhn-Tucker)条件,即要求:
{ α i ≥ 0 ; y i f ( x i ) − 1 ≥ 0 ; α i ( y i f ( x i ) − 1 ) = 0. \left\{ \begin{array}{rl} & \alpha _i\ge 0 ; \\ & y_if(x_i)-1 \ge 0; \\ & \alpha _i(y_if(x_i)-1)=0. \end{array} \right. ⎩⎨⎧αi≥0;yif(xi)−1≥0;αi(yif(xi)−1)=0.
2.3 非线性类问题——核技巧(kernel trick)
先来看一个视频,直观感受一下:SVM with polynomial 可视化
对于原始样本空间不是线性可分的情况,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
令 ϕ ( x ) \phi(x) ϕ(x) 表示将 x x x 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为:
f ( x ) = ω T ϕ ( x ) + b f(x) = \omega ^T \phi(x)+b f(x)=ωTϕ(x)+b
类似式(1),有:
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T ϕ ( x i ) + b ) ≥ 1 , i = 1 , 2 , . . . , m . \min \limits_{w,b} \ \ \frac{1}{2}\parallel w \parallel^2 \qquad s.t. \ \ y_i(w^T \phi(x_i) +b) \ge 1, \ i=1,2,...,m. w,bmin 21∥w∥2s.t. yi(wTϕ(xi)+b)≥1, i=1,2,...,m.
其对偶问题是:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i ) T ϕ ( x j ) s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 , i = 1 , 2 , . . . , m \max \limits_{\alpha }\sum \limits_{i=1}^m \alpha _i - \frac{1}{2}\sum \limits_{i=1}^m \sum \limits_{j=1}^m \alpha _i\alpha _j y_i y_j \phi(x_i)^T \phi(x_j) \\ s.t. \ \sum \limits_{i=1}^m \alpha _i y_i=0, \ \alpha _i \ge 0, i=1,2,...,m αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xi)Tϕ(xj)s.t. i=1∑mαiyi=0, αi≥0,i=1,2,...,m
若遇到高维或无穷维问题,求解 ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T \phi(x_j) ϕ(xi)Tϕ(xj) 会很困难,而利用核函数 κ ( ⋅ , ⋅ ) \kappa(\cdot,\cdot) κ(⋅,⋅) ,可避免这个问题:
κ ( x i , x j ) = ⟨ ϕ ( x i ) , ϕ ( x j ) ⟩ = ϕ ( x i ) T ϕ ( x j ) \kappa(x_i,x_j)=\left \langle \phi(x_i),\phi(x_j) \right \rangle=\phi(x_i)^T \phi(x_j) κ(xi,xj)=⟨ϕ(xi),ϕ(xj)⟩=ϕ(xi)Tϕ(xj)
求解后即可得到:
f ( x ) = ω T ϕ ( x ) + b = ∑ i = 1 m α i y i ϕ ( x i ) T ϕ ( x j ) + b = ∑ i = 1 m α i y i κ ( x , x i ) + b f(x) = \omega ^T \phi(x)+b = \sum \limits_{i=1}^m \alpha _i y_i \phi(x_i)^T \phi(x_j)+b = \sum \limits_{i=1}^m \alpha _i y_i \kappa(x,x_i) + b f(x)=ωTϕ(x)+b=i=1∑mαiyiϕ(xi)Tϕ(xj)+b=i=1∑mαiyiκ(x,xi)+b
常用核函数
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i T x j \kappa(x_i,x_j)=x_i^Tx_j κ(xi,xj)=xiTxj | |
| 多项式核 | κ ( x i , x j ) = ( x i T x j ) d \kappa(x_i,x_j)=(x_i^Tx_j)^d κ(xi,xj)=(xiTxj)d | d ≥ 1 d \ge1 d≥1 为多项式的次数 |
| 高斯核 | κ ( x i , x j ) = exp ( − ∥ x i − x j ∥ 2 2 σ 2 ) \kappa(x_i,x_j)= \exp (-\frac{\left \| x_i - x_j \right \|^2}{2 \sigma^2}) κ(xi,xj)=exp(−2σ2∥xi−xj∥2) | σ > 0 \sigma>0 σ>0 为高斯核的带宽(width) |
| 拉普拉斯核 | κ ( x i , x j ) = exp ( − ∥ x i − x j ∥ σ ) \kappa(x_i,x_j)=\exp (-\frac{\left \| x_i -x_j\right \|}{\sigma}) κ(xi,xj)=exp(−σ∥xi−xj∥) | σ > 0 \sigma>0 σ>0 |
| Sigmoid 核 | κ ( x i , x j ) = tanh ( β x i T x j + θ ) \kappa(x_i,x_j)=\tanh(\beta x_i^Tx_j+\theta) κ(xi,xj)=tanh(βxiTxj+θ) | tanh \tanh tanh 为双曲正切函数, β > 0 , θ < 0 \beta>0,\theta<0 β>0,θ<0 |
3 算法实现
麦子学院:深度学习基础介绍-机器学习
# SVM算法用于人脸识别步骤
# 1. 加载名人库数据,并获取数据参数
# 2. 将数据划分为训练集与测试集
# 3. 以数据样本做PCA降维
# 4. 建立SVM模型
# 5. 模型评估及可视化
from __future__ import print_function
from time import time # 用于每一步的计时
import logging # 打印程序进展信息
import matplotlib.pyplot as plt # 绘图
from sklearn.model_selection import train_test_split # 训练集测试集分开
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import RandomizedPCA
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.svm import SVC
print(__doc__)
# Display progress logs on stdout 在标准输出上显示进度日志
logging.basicConfig(level=logging.INFO, format=' %(asctime)s %(message)s')
##########################################################################
# Download the data, if not already on disk and load it as numpy arrays
# 如果磁盘上没有的话下载数据,并将其以向量格式加载
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4) # 下载名人数据集,lfw_people类似于字典结构
# introspect the images arrays to find the shapes (for plotting)
# 内省图像数组以找到形状(用于绘图)
n_samples, h, w =lfw_people.images.shape # 返回样本数
# for machine learning we use the 2 data directly (as relative pixel)
# positions info is ignored by this model
# 对于机器学习我们直接使用2个数据(作为相对像素)
# 此模型会忽略位置信息
X = lfw_people.data # 提取特征属性,每一行是一个实例,每一列是一个特征值
n_features = X.shape[1] # 获取维度,返回列数
# the label to predict is the id of the person
y = lfw_people.target # 返回对应数据集的标记
target_names = lfw_people.target_names # 返回类别名字
n_classes = target_names.shape[0] # 获得人脸识别数量
print("Total dataset size:")
print("n_samples: %d" % n_samples) # 打印实例个数
print("n_features: %d" % n_features) # 打印特征向量个数
print("n_classes: %d" % n_classes) # 打印人脸识别数量(类)
#########################################################################
# Split into a training set and a test set using a stratified k fold
# split into a training and testing set 划分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25)
###########################数据降维######################################
# Compute a PCA (eigenfaces) on the face dataset (treated as unlabeled
# datadet): unsupervised feature extrction / dimensionality reduction
n_components = 150 # 主成元素数量
print("Extrcting the top %d eigenfaces from %d faces"
% (n_components, X_train.shape[0]))
t0 = time()
pca = RandomizedPCA(n_components=n_components, whiten=True).fit(X_train) # 调用随机PCA方法,用X_train矩阵进行建模
print("done in %0.3fs" % (time() - t0))
eigenfaces = pca.components_.reshape((n_components, h, w)) # 人脸识别中提取特征值
print("Projecting the input data on the eigenfaces orthonoemal basis")
t0 = time()
X_train_pca = pca.transform(X_train) # 通过PCA将X_train转化为一个低维矩阵
X_test_pca = pca.transform(X_test) # 通过PCA将X_test 转化为一个低维矩阵
print("done in %0.3fs" % (time() - t0))
#########################################################################
# Train a SVM classification model 建立SVM模型
print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C':[1e3, 5e3, 1e4, 5e4, 1e5],
'gamma':[0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], } # C:penalty 惩罚项,gamma:针对核函数特征点使用比例
clf = GridSearchCV(SVC(kernel='rbf', class_weight=None), param_grid) # 遍历各种组合,rbf针对图像
clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_) # 打印最优组合
###########################评估+可视化##########################################
# Quantitative evaluation of the model quality on the test set
print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca) # 预测新数据
print("done in %0.3fs" % (time() - t0))
print(classification_report(y_test, y_pred, target_names=target_names)) # 真实标签与预测标签作比较
print(confusion_matrix(y_test, y_pred, labels=range(n_classes))) # 建立矩阵,对角线为预测正确
###############################################################################
# Qualitative evaluation of the predictions using matplotlib
def plot_gallery(images, titles, h, w, n_row=3, n_col=4): # 绘图
"""Helper function to plot a gallery of portraits"""
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row)) # 建立一个图
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
# plot the result of the prediction on a portion of the test set
def title(y_pred, y_test, target_names, i): # 将预测与实际标签打印出来
pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
return 'predicted: %s\n true: %s' % (pred_name, true_name)
prediction_titles = [title(y_pred, y_test, target_names, i)
for i in range(y_pred.shape[0])]
plt.figure(1)
plot_gallery(X_test, prediction_titles, h, w)
# plot the gallery of the most significative eigenfaces 绘制提取出的特征值的图
plt.figure(2)
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)
plt.show()
输出:
| 输入图像 | 输出图像 |
|---|---|
 |
 |
precision recall f1-score support
Ariel Sharon 0.52 0.61 0.56 18
Colin Powell 0.75 0.84 0.80 58
Donald Rumsfeld 0.82 0.70 0.75 33
George W Bush 0.88 0.87 0.88 133
Gerhard Schroeder 0.76 0.73 0.75 26
Hugo Chavez 0.95 0.75 0.84 24
Tony Blair 0.78 0.83 0.81 30
avg / total 0.82 0.81 0.81 322
[[ 11 4 0 2 1 0 0]
[ 1 49 2 4 0 0 2]
[ 3 2 23 5 0 0 0]
[ 4 6 2 116 2 1 2]
[ 0 1 1 2 19 0 3]
[ 1 3 0 1 1 18 0]
[ 1 0 0 2 2 0 25]]
参考资料:
[1] 周志华. 机器学习 : = Machine learning[M]. 清华大学出版社, 2016.
[2] 李航. 统计学习方法[M]. 清华大学出版社, 2012.
[3] 麦子学院:深度学习基础介绍-机器学习:http://www.maiziedu.com/course/373/
[4] 知乎:支持向量机(SVM)是什么意思?