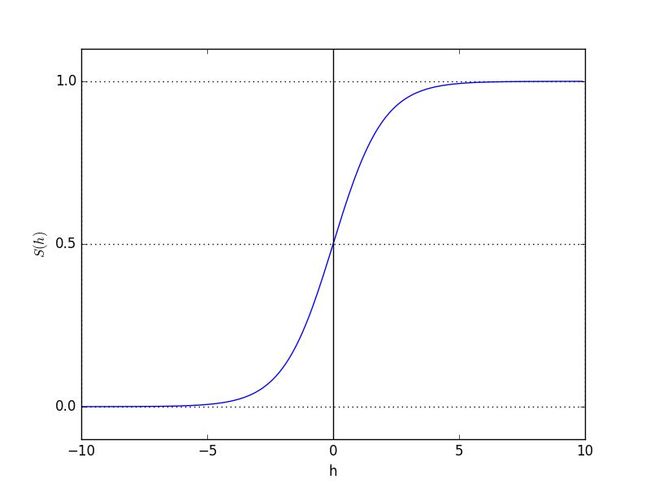
Sigmod函数
logist回归首先是一种分类方法,作为一种分类方法,它具有一个先验概率分布:伯努利分布。因此Sigmod函数具有同指数族分布一样的形式。
![][equtation1]
[equtation1]: http://latex.codecogs.com/svg.latex?\sigma=\frac{1}{1+{e^{-z}}}
复习:指数组分布有哪些?
- 伯努利分布(Bernoulli);
- 多项式分布(Multinomial);
- 泊松分布(Poisson);
- 伽马分布(gamma)与指数分布(exponential):对有间隔的正数进行建模,比如公交车的到站时间问题;
- β 分布:对小数建模;
- Dirichlet 分布:对概率分布进建模;
- Wishart 分布:协方差矩阵的分布;
- 高斯分布(Gaussian);
上面这些分布都可以化为Sigmod函数的形式,关于这些分布的问题,可以被归为广义线性模型。
观察图像可知,Sigmod函数看起来表现为一个阶跃函数的形式,sigmoid函数是一个良好的阈值函数。具有如下优点:
- 连续,光滑
- 严格单调
- 关于(0,0.5)中心对称
- 对阈值函数f(x)的近似得很良好
1, x > 0
/
f(x)=
\
0, x < 0
- 其导数f'(x)=f(x)*[1-f(x)],可以节约计算时间
我们可以据此给每个特征都乘上一个回归系数,然后把所有结果相加,将这个总和带入z。
![][equtation1]
[equtation1]: http://latex.codecogs.com/svg.latex?\sigma=\frac{1}{1+{e^{-z}}}
其中:
![][equtation2]
[equtation2]: http://latex.codecogs.com/svg.latex?z=w_{0}x_{0}+w_{1}x_{1}+\cdots+w_{n}x_{n}
以向量形式表达就是:
![][equtation3]
[equtation3]: http://latex.codecogs.com/svg.latex?z=w^{T}x
于是我们可以找到一个最佳参数w,尽可能得使分类趋于理想的结果。这种通过训练数据找到分类界面的方法非常类似于线性回归,因此它也被叫做logistc回归。
神经网络中的激活函数
如何确定这个界面,也就是找到w这组最佳系数,方法同线性回归类似,有最小二乘、梯度上升等方法,前者不再赘述,这里只说梯度上升(下降)法。
梯度上升法
首先要声明的是,梯度上升和梯度下降都是一回事,只是公式中的假发需要改为减法,原理都是沿着梯度找局部最优。原理在线性回归中已经写出来过,就不再赘述了,这里只介绍算法。
伪代码如下:
每个回归系数初始化为1
重复R次:
计算整个数据集的梯度
是有alpha*gradient更新回归系数的向量
返回回归系数
代码实例:
MLR已经替我们把数据已经洗好了,首先预览一下:
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
可以看到第一列是x1,第二列为x2,最后一列是类别。
总之代码如下:
# -*-coding:utf-8 -*-
from numpy import *
#数据载入函数
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
#Sigmoid函数
def sigmoid(inX):
return 1.0/(1+exp(-inX))
#梯度下降函数
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #搞成NumPy矩阵
labelMat = mat(classLabels).transpose()
m,n = shape(dataMatrix) #m行n列
alpha = 0.001 #定义步长
maxCycles = 500 #迭代次数
weights = ones((n,1)) #初始化w,一个全是1的列向量
for k in range(maxCycles): #循环固定次数
h = sigmoid(dataMatrix*weights)
#h是一个列向量,维度等于样本个数,该数据有100个
error = (labelMat - h) #算个差值
weights = weights + alpha * dataMatrix.transpose()* error
#按照差值的方向调整系数
return weights
if __name__ == '__main__':
dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
print weights
返回值也可以看一下:
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
当然我们没有忘记可视化是很重要的,于是我们试着画个图看看:
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
if __name__ == '__main__':
dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
print weights
plotBestFit(weights.getA())
#getA()是np矩阵方法,作为ndarray返回自己
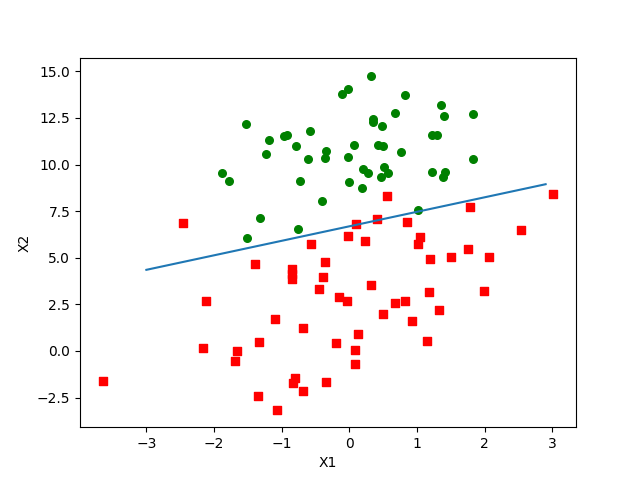
得到下图:
这个方法好是挺好的,但因为用了300次乘法,所以不太适用于较大数据,所以我们再来搞个随机梯度看看。
随机梯度上升(Stochastic Gradient)
首先,单纯的梯度上升在每次更新w时都需要遍历整个数据集,小数据尚可,对于大数据没什么可行性,对于这种算法我们把它叫做批处理。
相对应的,还有一种算法我们每次更新仅用一个样本点,这种方法叫做在线学习。
伪代码:
所有回归系数初始化为1
对数据集中每个样本
计算该样本的梯度
使用alpha*gradient更新回归系数值
返回回归系数值
代码如下:
def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #初始化w,一个全是1的行向量
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
if __name__ == '__main__':
weights2 = stocGradAscent0(array(dataArr), labelMat)
print weights2
plotBestFit(weights2)
看看返回的w,好像跟第一个相差很大啊。
[ 1.01702007 0.85914348 -0.36579921]
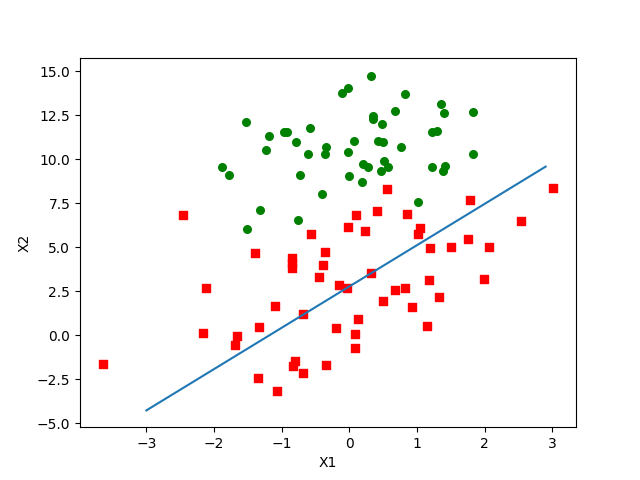
画的图也完全不能接受啊,肯定是哪里出了问题。
仔细思考一下,这个算法到底哪里出了问题?原来是步长的问题!!
步长过小,收敛太慢;步长太小,收敛不到局部最优解。
所以我们需要对算法改进一下,得到有一个动态步长。
#默认迭代次数是150次,可以通过参数修改
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix)
weights = ones(n) #initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4/(1.0+j+i)+0.0001 #随着迭代步长减小,但由于常数项不会太小
randIndex = int(random.uniform(0,len(dataIndex)))#从而保证后面的数据也有一定影响力
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
#每次从列表中随机选一个值,然后删掉
return weights
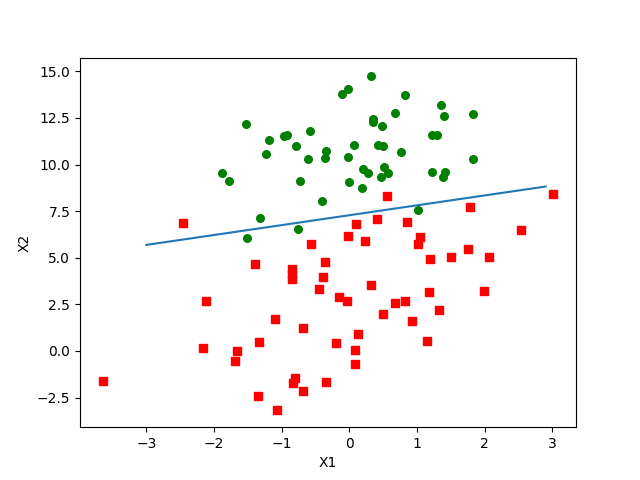
最后得到的结果是:
[ 13.10360032 0.65123109 -1.75151716]
好像还能接受。