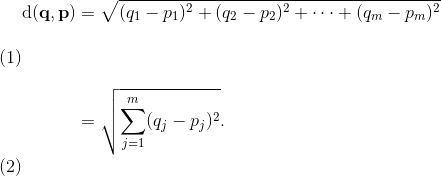SciPyCon 2018 sklearn 教程(下)
原文:SciPy 2018 Scikit-learn Tutorial
译者:飞龙
协议:CC BY-NC-SA 4.0
自豪地采用谷歌翻译
十三、交叉验证和得分方法
在前面的章节和笔记本中,我们将数据集分为两部分:训练集和测试集。 我们使用训练集来拟合我们的模型,并且我们使用测试集来评估其泛化能力 - 它对新的,没见过的数据的表现情况。
然而,(标记的)数据通常是宝贵的,这种方法让我们只将约 3/4 的数据用于行训练。 另一方面,我们只会尝试将我们的 1/4 数据应用于测试。 使用更多数据来构建模型,并且获得更加鲁棒的泛化能力估计,常用方法是交叉验证。 在交叉验证中,数据被重复拆分为非重叠的训练和测试集,并为每对建立单独的模型。 然后聚合测试集的得分来获得更鲁棒的估计。
进行交叉验证的最常用方法是k折交叉验证,其中数据首先被分成k(通常是 5 或 10)个相等大小的折叠,然后对于每次迭代,使用k折中的一个作为测试数据,其余作为训练数据:
这样,每个数据点只在测试集中一次,我们可以使用第k个数据之外的所有数据进行训练。 让我们应用这种技术,在鸢尾花数据集上评估KNeighborsClassifier算法:
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
iris = load_iris()
X, y = iris.data, iris.target
classifier = KNeighborsClassifier()
鸢尾花中的标签是有序的,这意味着如果我们像上面那样拆分数据,第一个折叠只有标签 0,而最后一个只有标签 2:
y
为了在评估中避免这个问题,我们首先将我们的数据打乱:
import numpy as np
rng = np.random.RandomState(0)
permutation = rng.permutation(len(X))
X, y = X[permutation], y[permutation]
print(y)
现在实现交叉验证很简单:
k = 5
n_samples = len(X)
fold_size = n_samples // k
scores = []
masks = []
for fold in range(k):
# 为此折叠中的测试集生成一个布尔掩码
test_mask = np.zeros(n_samples, dtype=bool)
test_mask[fold * fold_size : (fold + 1) * fold_size] = True
# 为可视化存储掩码
masks.append(test_mask)
# 使用此掩码创建训练和测试集
X_test, y_test = X[test_mask], y[test_mask]
X_train, y_train = X[~test_mask], y[~test_mask]
# 拟合分类器
classifier.fit(X_train, y_train)
# 计算得分并记录
scores.append(classifier.score(X_test, y_test))
让我们检查一下我们的测试掩码是否正确:
import matplotlib.pyplot as plt
%matplotlib inline
plt.matshow(masks, cmap='gray_r')
现在让我们看一下我们计算出的得分:
print(scores)
print(np.mean(scores))
正如你所看到的,得分广泛分布于 90% 正确到 100% 正确。 如果我们只进行一次分割,我们可能会得到任何答案。
由于交叉验证是机器学习中常见的模式,有个函数执行上面的操作,带有更多灵活性和更少代码。sklearn.model_selection模块具有交叉验证相关的所有函数。 最简单的函数是cross_val_score,它接受估计器和数据集,并将为你完成所有拆分:
from sklearn.model_selection import cross_val_score
scores = cross_val_score(classifier, X, y)
print('Scores on each CV fold: %s' % scores)
print('Mean score: %0.3f' % np.mean(scores))
如你所见,该函数默认使用三个折叠。 你可以使用cv参数更改折叠数:
cross_val_score(classifier, X, y, cv=5)
交叉验证模块中还有辅助对象,它们将为你生成各种不同交叉验证方法的索引,包括 k-fold:
from sklearn.model_selection import KFold, StratifiedKFold, ShuffleSplit
默认情况下,cross_val_score将StratifiedKFold用于分类,这可确保数据集中的类比例反映在每个折叠中。 如果你有一个二分类数据集,其中 90% 的数据点属于类 0,那么这意味着在每个折叠中,90% 的数据点将属于类 0。如果你只是使用KFold交叉验证,你可能会生成一个只包含类 0 的分割。每当你进行分类时,通常最好使用StratifiedKFold。
StratifiedKFold也消除了我们打乱鸢尾花的需要。 让我们看看在未打乱的鸢尾花数据集上,它生成什么类型的折叠。 每个交叉验证类都是训练和测试索引的集合的生成器:
cv = StratifiedKFold(n_splits=5)
for train, test in cv.split(iris.data, iris.target):
print(test)
正如你所看到的,在每个折叠中,在开始,中间,和结束位置,都有一些样本。 这样,保留了类别比例。 让我们观察一下split:
def plot_cv(cv, features, labels):
masks = []
for train, test in cv.split(features, labels):
mask = np.zeros(len(labels), dtype=bool)
mask[test] = 1
masks.append(mask)
plt.matshow(masks, cmap='gray_r')
plot_cv(StratifiedKFold(n_splits=5), iris.data, iris.target)
为了比较,仍旧是标准KFold,忽略标签:
plot_cv(KFold(n_splits=5), iris.data, iris.target)
请记住,增加折叠数量会为你提供更大的训练数据集,但会导致更多重复,因此评估速度会变慢:
plot_cv(KFold(n_splits=10), iris.data, iris.target)
另一个有用的交叉验证生成器是ShuffleSplit。 该生成器简单地重复分割数据的随机部分。 这允许用户独立指定重复次数和训练集大小:
plot_cv(ShuffleSplit(n_splits=5, test_size=.2), iris.data, iris.target)
如果你想要更鲁棒的估计,你可以增加分割数量:
plot_cv(ShuffleSplit(n_splits=20, test_size=.2), iris.data, iris.target)
你可以使用cross_val_score方法来使用所有这些交叉验证生成器:
cv = ShuffleSplit(n_splits=5, test_size=.2)
cross_val_score(classifier, X, y, cv=cv)
练习
在鸢尾花数据集上,使用
KFold类进行三折交叉验证,而不打乱数据。你能解释一下结果吗?
# %load solutions/13_cross_validation.py
十四、参数选择、验证和测试
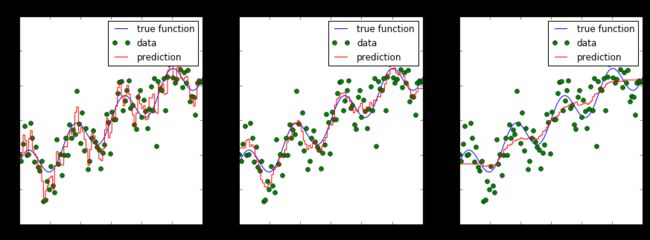
大多数模型的参数会影响他们可以学习的模型的复杂程度。回忆使用KNeighborsRegressor的时候。 如果我们改变我们考虑的邻居数量,我们会得到更平滑的预测:
在上图中,我们看到n_neighbors的三个不同值。对于n_neighbors = 2,数据过拟合,模型过于灵活,可以适应训练数据中的噪声。对于n_neighbors = 20,模型不够灵活,无法合理建模数据中的变化。
在中间,对于n_neighbors = 5,我们找到了一个很好的中点。它非常适合数据,并且不会受到任何一个图中所见的,过拟合或欠拟合问题的影响。我们想要的是一种定量识别过拟合和欠拟合的方法,并优化超参数(这种情况是多项式次数d)来确定最佳算法。
我们要权衡过多记录训练数据的特殊性和噪声,或者没有建模足够的可变性。这是一个需要在基本上每个机器学习应用中做出的权衡,并且是一个核心概念,称为偏差 - 方差 - 权衡或“过拟合与欠拟合”。
超参数、过拟合和欠拟合
遗憾的是,没有找到最佳位置的一般规则,因此机器学习实践者必须通过尝试几个超参数设置,来找到模型复杂性和泛化的最佳权衡。 超参数是机器学习算法的内部旋钮或可调参数(与算法从训练数据中学习的模型参数相反 - 例如,线性回归模型的权重系数);K 近邻中的k的数量是这样的超参数。
最常见的是,这种“超参数调整”是使用暴力搜索完成的,例如在多个n_neighbors值上:
from sklearn.model_selection import cross_val_score, KFold
from sklearn.neighbors import KNeighborsRegressor
# 生成玩具数据集
x = np.linspace(-3, 3, 100)
rng = np.random.RandomState(42)
y = np.sin(4 * x) + x + rng.normal(size=len(x))
X = x[:, np.newaxis]
cv = KFold(shuffle=True)
# 对每个参数设置执行交叉验证
for n_neighbors in [1, 3, 5, 10, 20]:
scores = cross_val_score(KNeighborsRegressor(n_neighbors=n_neighbors), X, y, cv=cv)
print("n_neighbors: %d, average score: %f" % (n_neighbors, np.mean(scores)))
scikit-learn 中有一个函数,称为validation_plot,用于重现上面的卡通图。 它根据训练和验证误差(使用交叉验证)绘制一个参数,例如邻居的数量:
from sklearn.model_selection import validation_curve
n_neighbors = [1, 3, 5, 10, 20, 50]
train_scores, test_scores = validation_curve(KNeighborsRegressor(), X, y, param_name="n_neighbors",
param_range=n_neighbors, cv=cv)
plt.plot(n_neighbors, train_scores.mean(axis=1), label="train accuracy")
plt.plot(n_neighbors, test_scores.mean(axis=1), label="test accuracy")
plt.ylabel('Accuracy')
plt.xlabel('Number of neighbors')
plt.xlim([50, 0])
plt.legend(loc="best");
请注意,许多邻居意味着“平滑”或“简单”的模型,因此绘图使用还原的x轴。
如果多个参数很重要,例如 SVM 中的参数C和gamma(稍后会详细介绍),则尝试所有可能的组合:
from sklearn.model_selection import cross_val_score, KFold
from sklearn.svm import SVR
# 对每个参数设置执行交叉验证
for C in [0.001, 0.01, 0.1, 1, 10]:
for gamma in [0.001, 0.01, 0.1, 1]:
scores = cross_val_score(SVR(C=C, gamma=gamma), X, y, cv=cv)
print("C: %f, gamma: %f, average score: %f" % (C, gamma, np.mean(scores)))
由于这是一种非常常见的模式,因此在 scikit-learn 中有一个内置类GridSearchCV。 GridSearchCV接受描述应该尝试的参数的字典,和一个要训练的模型。
参数网格被定义为字典,其中键是参数,值是要测试的设置。
要检查不同折叠的训练得分,请将参数return_train_score设置为True。
from sklearn.model_selection import GridSearchCV
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10], 'gamma': [0.001, 0.01, 0.1, 1]}
grid = GridSearchCV(SVR(), param_grid=param_grid, cv=cv, verbose=3, return_train_score=True)
GridSearchCV的一大优点是它是一个元估计器。 它需要像上面的 SVR 这样的估计器,并创建一个新的估计器,其行为完全相同 - 在这种情况下,就像一个回归器。 所以我们可以调用它的fit来训练:
grid.fit(X, y)
fit所做的比我们上面做的复杂得多。 首先,它使用交叉验证运行相同的循环,来找到最佳参数组合。 一旦它具有最佳组合,它在所有传给fit的数据上再次执行fit(无交叉验证),来使用最佳参数设置构建单个新模型。
然后,与所有模型一样,我们可以使用predict或score:
grid.predict(X)
你可以在best_params_属性中检查GridSearchCV找到的最佳参数,以及best_score_属性中的最佳得分:
print(grid.best_score_)
print(grid.best_params_)
但是,你可以通过访问cv_results_属性来调查每组参数值的表现和更多信息。 cv_results_属性是一个字典,其中每个键都是字符串,每个值都是数组。 因此,它可以用于制作pandas DataFrame。
type(grid.cv_results_)
print(grid.cv_results_.keys())
import pandas as pd
cv_results = pd.DataFrame(grid.cv_results_)
cv_results.head()
cv_results_tiny = cv_results[['param_C', 'param_gamma', 'mean_test_score']]
cv_results_tiny.sort_values(by='mean_test_score', ascending=False).head()
但是,将这个得分用于评估存在问题。 你可能会犯所谓的多假设检验错误。 如果你尝试了很多参数设置,其中一些参数设置只是偶然表现很好,而你获得的得分可能无法反映你的模型对新的没见过的数据的表现。 因此,在执行网格搜索之前拆分单独的测试集是很好的。 这种模式可以看作是训练-验证-测试分割,在机器学习中很常见:
我们可以非常容易地实现,通过使用train_test_split分割一些测试数据,在训练集上训练GridSearchCV,并将score方法应用于测试集:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10], 'gamma': [0.001, 0.01, 0.1, 1]}
cv = KFold(n_splits=10, shuffle=True)
grid = GridSearchCV(SVR(), param_grid=param_grid, cv=cv)
grid.fit(X_train, y_train)
grid.score(X_test, y_test)
我们还可以查看所选的参数:
grid.best_params_
一些实践者采用更简单的方案,将数据简单地分为三个部分,即训练,验证和测试。 如果你的训练集非常大,或者使用交叉验证训练许多模型是不可行的,因为训练模型需要很长时间,这是一种可能的替代方案。 你可以使用 scikit-learn 执行此操作,例如通过拆分测试集,然后将GridSearchCV与ShuffleSplit交叉验证应用于单次迭代:
from sklearn.model_selection import train_test_split, ShuffleSplit
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10], 'gamma': [0.001, 0.01, 0.1, 1]}
single_split_cv = ShuffleSplit(n_splits=1)
grid = GridSearchCV(SVR(), param_grid=param_grid, cv=single_split_cv, verbose=3)
grid.fit(X_train, y_train)
grid.score(X_test, y_test)
这要快得多,但可能会产生更糟糕的超参数,从而产生更糟糕的结果。
clf = GridSearchCV(SVR(), param_grid=param_grid)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
练习
应用网格搜索来查找
KNeighborsClassifier中邻居数量的最佳设置,并将其应用于数字数据集。
十五、估计器流水线
在本节中,我们将研究如何链接不同的估计器。
简单示例:估计器之前的特征提取和选择
特征提取:向量化器
对于某些类型的数据,例如文本数据,必须应用特征提取步骤将其转换为数值特征。 为了说明,我们加载我们之前使用的 SMS 垃圾邮件数据集。
import os
with open(os.path.join("datasets", "smsspam", "SMSSpamCollection")) as f:
lines = [line.strip().split("\t") for line in f.readlines()]
text = [x[1] for x in lines]
y = [x[0] == "ham" for x in lines]
from sklearn.model_selection import train_test_split
text_train, text_test, y_train, y_test = train_test_split(text, y)
以前,我们手动应用了特征提取,如下所示:
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model import LogisticRegression
vectorizer = TfidfVectorizer()
vectorizer.fit(text_train)
X_train = vectorizer.transform(text_train)
X_test = vectorizer.transform(text_test)
clf = LogisticRegression()
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
我们学习转换然后将其应用于测试数据的情况,在机器学习中非常常见。 因此 scikit-learn 有一个快捷方式,称为流水线:
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(TfidfVectorizer(), LogisticRegression())
pipeline.fit(text_train, y_train)
pipeline.score(text_test, y_test)
如你所见,这使代码更短,更容易处理。 在背后,与上面完全相同。 当在水流上调用fit时,它将依次调用每个步骤的fit。
在第一步的fit之后,它将使用第一步的transform方法来创建新的表示。 然后将其用于下一步的fit,依此类推。 最后,在最后一步,只调用fit。
如果我们调用score,那么每一步都只会调用transform - 毕竟这可能是测试集! 然后,在最后一步,使用新的表示调用score。 predict也是如此。
流水线的构建不仅简化了代码,而且对于模型选择也很重要。 假设我们想要网格搜索C来调整上面的 Logistic 回归。
让我们假设我们这样做:
# This illustrates a common mistake. Don't use this code!
from sklearn.model_selection import GridSearchCV
vectorizer = TfidfVectorizer()
vectorizer.fit(text_train)
X_train = vectorizer.transform(text_train)
X_test = vectorizer.transform(text_test)
clf = LogisticRegression()
grid = GridSearchCV(clf, param_grid={'C': [.1, 1, 10, 100]}, cv=5)
grid.fit(X_train, y_train)
我们哪里做错了?
在这里,我们使用X_train上的交叉验证进行了网格搜索。 然而,当应用TfidfVectorizer时,它看到了所有的X_train,而不仅仅是训练折叠! 因此,它可以使用测试折叠中单词频率的知识。 这被称为测试集的“污染”,并且使泛化性能或错误选择的参数的估计过于乐观。 我们可以通过流水线解决这个问题:
from sklearn.model_selection import GridSearchCV
pipeline = make_pipeline(TfidfVectorizer(),
LogisticRegression())
grid = GridSearchCV(pipeline,
param_grid={'logisticregression__C': [.1, 1, 10, 100]}, cv=5)
grid.fit(text_train, y_train)
grid.score(text_test, y_test)
请注意,我们需要告诉流水线我们要在哪一步设置参数C。我们可以使用特殊的__语法来完成此操作。 __之前的名称只是类的名称,__之后的部分是我们想要使用网格搜索设置的参数。
使用流水线的另一个好处是,我们现在还可以使用GridSearchCV搜索特征提取的参数:
from sklearn.model_selection import GridSearchCV
pipeline = make_pipeline(TfidfVectorizer(), LogisticRegression())
params = {'logisticregression__C': [.1, 1, 10, 100],
"tfidfvectorizer__ngram_range": [(1, 1), (1, 2), (2, 2)]}
grid = GridSearchCV(pipeline, param_grid=params, cv=5)
grid.fit(text_train, y_train)
print(grid.best_params_)
grid.score(text_test, y_test)
练习
使用
StandardScaler和RidgeRegression创建流水线,并将其应用于波士顿住房数据集(使用sklearn.datasets.load_boston加载)。 尝试添加sklearn.preprocessing.PolynomialFeatures变换器作为第二个预处理步骤,并网格搜索多项式的次数(尝试 1,2 和 3)。
# %load solutions/15A_ridge_grid.py
十六、模型评估、得分指标和处理不平衡类别
在之前的笔记本中,我们已经详细介绍了如何评估模型,以及如何选择最佳模型。 到目前为止,我们假设我们得到了表现的度量,它度量模型的质量。 但是,应该使用什么度量标准并不总是显而易见的。 scikit-learn 中的默认分数,对于分类是准确率,即正确分类的样本的比例,对于回归是 r2 得分,是确定系数。
在许多情况下,这些是合理的默认选择;但是,根据我们的任务,这些并不总是最终或推荐的选择。
让我们更详细地看一下分类,回到手写数字分类的应用。 那么,如何训练分类器并使用不同的方式进行评估呢? Scikit-learn 在 sklearn.metrics 模块中有许多有用的方法,可以帮助我们完成这项任务:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
np.set_printoptions(precision=2)
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
digits = load_digits()
X, y = digits.data, digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y,
random_state=1,
stratify=y,
test_size=0.25)
classifier = LinearSVC(random_state=1).fit(X_train, y_train)
y_test_pred = classifier.predict(X_test)
print("Accuracy: {}".format(classifier.score(X_test, y_test)))
在这里,我们正确预测了 95.3% 的样本。 对于多类问题,通常很有趣的是,知道哪些类很难预测,哪些类很容易,或哪些类混淆了。 获取错误分类的更多信息的一种方法,是confusion_matrix,它为每个真正的类显示给定预测结果的频率。
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_test_pred)
绘图有时更可读:
plt.matshow(confusion_matrix(y_test, y_test_pred), cmap="Blues")
plt.colorbar(shrink=0.8)
plt.xticks(range(10))
plt.yticks(range(10))
plt.xlabel("Predicted label")
plt.ylabel("True label");
我们可以看到大多数条目都在对角线上,这意味着我们正确地预测了几乎所有样本。 非对角线的条目向我们显示许多 8 被归类为 1,并且 9 很可能与许多其他类混淆。
另一个有用的函数是classification_report,它为所有类提供精确率,召回率,f 得分和支持度。 精确率是一个类有多少预测实际上是那个类。 TP,FP,TN,FN 分别代表“真正例”,“假正例”,“真负例”和“假负例”:
Precision = TP / (TP + FP)
召回率是有多少真正例被复原:
Recall = TP / (TP + FN)
F1 得分是二者的调和均值:
F1 = 2 x (precision x recall) / (precision + recall)
上述所有这些值的值都在闭区间[0,1]中,其中 1 表示完美得分。
from sklearn.metrics import classification_report
print(classification_report(y_test, y_test_pred))
这些指标有助于实践中经常出现的两种特殊情况:
- 不平衡类别,即一个类可能比另一个类更频繁。
- 非对称成本,即一种错误比另一种更“昂贵”。
首先我们来看看第一个。 假设我们有 1:9 的不平衡类别,这是相当温和的(想想广告点击预测,只有 0.001% 的广告可能会被点击):
np.bincount(y) / y.shape[0]
作为一个玩具示例,假设我们想要划分数字三和所有其他数字:
X, y = digits.data, digits.target == 3
现在我们在分类器上运行交叉验证,看看它有多好:
我们的分类器准确率为 90%。 这样好吗? 还是不好? 请记住,90% 的数据“不是三”。 因此,让我们看看虚拟分类器的表现如何,它始终预测最频繁的类:
from sklearn.dummy import DummyClassifier
cross_val_score(DummyClassifier("most_frequent"), X, y)
也是 90%(正如预期的那样)! 所以有一种可能,我们的分类器不是很好,它并不比一个甚至不看数据的简单策略更好。 不过,这个判断太快了。 准确性根本不是评估不平衡数据集的分类器的好方法!
np.bincount(y) / y.shape[0]
ROC 曲线
更好的衡量标准是使用所谓的 ROC(受试者工作特性)曲线。 ROC 曲线处理分类器的不确定性输出,比如我们上面训练的 SVC 的“决策函数”。 它不是在 0 处截断并查看分类结果,而是查看每个可能的截断值并记录有多少真正例预测,以及有多少假正例预测。
下图比较了在“三和其它”任务上,我们的分类器的三个参数设置的 roc 曲线。
from sklearn.metrics import roc_curve, roc_auc_score
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
for gamma in [.05, 0.1, 0.5]:
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate (recall)")
svm = SVC(gamma=gamma).fit(X_train, y_train)
decision_function = svm.decision_function(X_test)
fpr, tpr, _ = roc_curve(y_test, decision_function)
acc = svm.score(X_test, y_test)
auc = roc_auc_score(y_test, svm.decision_function(X_test))
label = "gamma: %0.3f, acc:%.2f auc:%.2f" % (gamma, acc, auc)
plt.plot(fpr, tpr, label=label, linewidth=3)
plt.legend(loc="best");
由于决策阈值非常小,假正例很低,但假负例也很少,但是阈值非常高的话,真正例率和假负例率都很高。所以一般来说,曲线将从左下角到右上角。对角线反映了机会表现,而目标是尽可能在左上角。这意味着与任何负样本相比,为所有正样本提供更高的decision_function值。
在这个意义上,该曲线仅考虑正样本和负样本的排名,而不是实际值。从图例中的曲线和准确率值可以看出,即使所有分类器具有相同的准确率,89%,甚至低于虚拟分类器,其中一个具有完美的 roc 曲线,而其中一个表现出机会水平。
对于网格搜索和交叉验证,我们通常希望将模型评估压缩为单个数字。使用 roc 曲线的一个好方法是使用曲线下面积(AUC)。我们可以通过指定scoring ="roc_auc"在cross_val_score中使用它:
from sklearn.model_selection import cross_val_score
cross_val_score(SVC(gamma='auto'), X, y, scoring="roc_auc", cv=5)
内建和自定义的得分函数
还有更多可用的评分方法,可用于不同类型的任务。 你可以在SCORERS字典中找到它们。 唯一的文档解释了所有这些。
from sklearn.metrics.scorer import SCORERS
print(SCORERS.keys())
你也可以定义自己的得分指标。 你可以提供一个可调用对象作为scoring参数,而不是字符串,即具有__call__方法对象或函数。 它需要接受模型,测试集特征X_test和测试集标签y_test,并返回一个浮点数。 更高的浮点意味着更好的模型。
让我们重新实现标准准确率得分:
def my_accuracy_scoring(est, X, y):
return np.mean(est.predict(X) == y)
cross_val_score(SVC(), X, y, scoring=my_accuracy_scoring)
练习
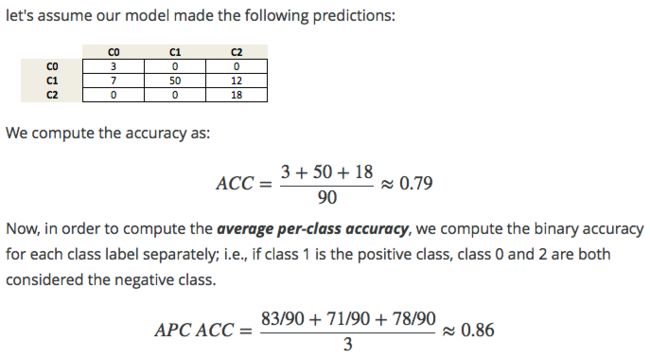
在前面的章节中,我们通常使用准确率度量来评估分类器的表现。 我们还没有谈到的相关措施是平均每类准确率(APCA)。 我们记得,准确性定义为:
ACC = (TP + TN) / n其中
n是样本总数。 这可以推广为:ACC = T / N其中
T是多类设置中所有正确预测的数量。给定以下“真实”类标签和预测类标签数组,你是否可以实现一个函数,使用准确率度量来计算平均每类准确率,如下所示?
y_true = np.array([0, 0, 0, 1, 1, 1, 1, 1, 2, 2])
y_pred = np.array([0, 1, 1, 0, 1, 1, 2, 2, 2, 2])
confusion_matrix(y_true, y_pred)
# %load solutions/16A_avg_per_class_acc.py
十七、深入:线性模型
线性模型在可用的数据很少时非常有用,或者对于文本分类中的非常大的特征空间很有用。 此外,它们是正则化的良好研究案例。
用于回归的线性模型
用于回归的所有线性模型学习系数参数coef_和偏移intercept_,来使用线性特征组合做出预测:
y_pred = x_test[0] * coef_[0] + ... + x_test[n_features-1] * coef_[n_features-1] + intercept_
回归的线性模型之间的差异在于,除了很好地拟合训练数据之外,对系数施加什么样的限制或惩罚,作为正则化。 最标准的线性模型是“普通最小二乘回归”,通常简称为“线性回归”。 它没有对coef_施加任何额外限制,因此当特征数量很大时,它会变得行为异常,并且模型会过拟合。
让我们生成一个简单的模拟,以查看这些模型的行为。
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
X, y, true_coefficient = make_regression(n_samples=200, n_features=30, n_informative=10, noise=100, coef=True, random_state=5)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=5, train_size=60, test_size=140)
print(X_train.shape)
print(y_train.shape)
线性回归
from sklearn.linear_model import LinearRegression
linear_regression = LinearRegression().fit(X_train, y_train)
print("R^2 on training set: %f" % linear_regression.score(X_train, y_train))
print("R^2 on test set: %f" % linear_regression.score(X_test, y_test))
from sklearn.metrics import r2_score
print(r2_score(np.dot(X, true_coefficient), y))
plt.figure(figsize=(10, 5))
coefficient_sorting = np.argsort(true_coefficient)[::-1]
plt.plot(true_coefficient[coefficient_sorting], "o", label="true")
plt.plot(linear_regression.coef_[coefficient_sorting], "o", label="linear regression")
plt.legend()
from sklearn.model_selection import learning_curve
def plot_learning_curve(est, X, y):
training_set_size, train_scores, test_scores = learning_curve(est, X, y, train_sizes=np.linspace(.1, 1, 20))
estimator_name = est.__class__.__name__
line = plt.plot(training_set_size, train_scores.mean(axis=1), '--', label="training scores " + estimator_name)
plt.plot(training_set_size, test_scores.mean(axis=1), '-', label="test scores " + estimator_name, c=line[0].get_color())
plt.xlabel('Training set size')
plt.legend(loc='best')
plt.ylim(-0.1, 1.1)
plt.figure()
plot_learning_curve(LinearRegression(), X, y)
岭回归(L2 惩罚)
岭估计器是普通LinearRegression的简单正则化(称为 l2 惩罚)。 特别是,它具有的优点是,在计算上不比普通的最小二乘估计更昂贵。
正则化的总数通过Ridge的alpha参数设置。
from sklearn.linear_model import Ridge
ridge_models = {}
training_scores = []
test_scores = []
for alpha in [100, 10, 1, .01]:
ridge = Ridge(alpha=alpha).fit(X_train, y_train)
training_scores.append(ridge.score(X_train, y_train))
test_scores.append(ridge.score(X_test, y_test))
ridge_models[alpha] = ridge
plt.figure()
plt.plot(training_scores, label="training scores")
plt.plot(test_scores, label="test scores")
plt.xticks(range(4), [100, 10, 1, .01])
plt.xlabel('alpha')
plt.legend(loc="best")
plt.figure(figsize=(10, 5))
plt.plot(true_coefficient[coefficient_sorting], "o", label="true", c='b')
for i, alpha in enumerate([100, 10, 1, .01]):
plt.plot(ridge_models[alpha].coef_[coefficient_sorting], "o", label="alpha = %.2f" % alpha, c=plt.cm.viridis(i / 3.))
plt.legend(loc="best")
调整alpha对表现至关重要。
plt.figure()
plot_learning_curve(LinearRegression(), X, y)
plot_learning_curve(Ridge(alpha=10), X, y)
Lasso(L1 惩罚)
Lasso估计器可用于对系数施加稀疏性。 换句话说,如果我们认为许多特征不相关,那么我们会更喜欢它。 这是通过所谓的 l1 惩罚来完成的。
from sklearn.linear_model import Lasso
lasso_models = {}
training_scores = []
test_scores = []
for alpha in [30, 10, 1, .01]:
lasso = Lasso(alpha=alpha).fit(X_train, y_train)
training_scores.append(lasso.score(X_train, y_train))
test_scores.append(lasso.score(X_test, y_test))
lasso_models[alpha] = lasso
plt.figure()
plt.plot(training_scores, label="training scores")
plt.plot(test_scores, label="test scores")
plt.xticks(range(4), [30, 10, 1, .01])
plt.legend(loc="best")
plt.figure(figsize=(10, 5))
plt.plot(true_coefficient[coefficient_sorting], "o", label="true", c='b')
for i, alpha in enumerate([30, 10, 1, .01]):
plt.plot(lasso_models[alpha].coef_[coefficient_sorting], "o", label="alpha = %.2f" % alpha, c=plt.cm.viridis(i / 3.))
plt.legend(loc="best")
plt.figure(figsize=(10, 5))
plot_learning_curve(LinearRegression(), X, y)
plot_learning_curve(Ridge(alpha=10), X, y)
plot_learning_curve(Lasso(alpha=10), X, y)
你也可以使用ElasticNet,而不是选择Ridge或Lasso,它使用两种形式的正则化,并提供一个参数来指定它们之间的权重。ElasticNet通常在这些模型中表现最佳。
用于分类的线性模型
用于分类的所有线性模型学习系数参数coef_和偏移intercept_,来使用线性特征组合做出预测:
y_pred = x_test[0] * coef_[0] + ... + x_test[n_features-1] * coef_[n_features-1] + intercept_ > 0
如你所见,这与回归非常相似,只是应用了零处的阈值。
同样,用于分类的线性模型之间的区别是,对coef_和intercept_施加什么类型的正则化,但是在如何测量训练集的拟合(所谓的损失函数)方面也存在微小差异。
线性分类的两种最常见的模型是LinearSVC实现的线性 SVM,和LogisticRegression。
线性分类器的正则化的良好直觉是,使用高正则化,如果大多数点被正确分类就足够了。 但使用较少的正则化,每个数据点的重要性也越来越高。这里使用具有不同C值的线性 SVM 来说明。
LinearSVC中C的影响
在LinearSVC中,C参数控制模型中的正则化。
较低的C产生更多的正则化和更简单的模型,而较高的C产生较少的正则化和来自各个数据点的更多影响。
from figures import plot_linear_svc_regularization
plot_linear_svc_regularization()
与Ridge/Lasso划分类似,你可以将penalty参数设置为'l1'来强制系数的稀疏性(类似于Lasso)或'l2'来鼓励更小的系数(类似于Ridge)。
多类线性分类
from sklearn.datasets import make_blobs
plt.figure()
X, y = make_blobs(random_state=42)
plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=plt.cm.tab10(y))
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
print(linear_svm.coef_.shape)
print(linear_svm.intercept_.shape)
plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=plt.cm.tab10(y))
line = np.linspace(-15, 15)
for coef, intercept in zip(linear_svm.coef_, linear_svm.intercept_):
plt.plot(line, -(line * coef[0] + intercept) / coef[1])
plt.ylim(-10, 15)
plt.xlim(-10, 8);
点以一对多(OVR)的方式分类(又名 OVA),我们将测试点分配给模型对测试点具有最高置信度的类(在 SVM 情况下,与分隔超平面的距离最大)。
练习
使用
LogisticRegression来分类数字数据集,并网格搜索C参数。
当你增加或减少alpha时,你认为上面的学习曲线如何变化? 尝试更改岭和Lasso中的alpha参数,看看你的直觉是否正确。
from sklearn.datasets import load_digits
from sklearn.linear_model import LogisticRegression
digits = load_digits()
X_digits, y_digits = digits.data, digits.target
# split the dataset, apply grid-search
# %load solutions/17A_logreg_grid.py
# %load solutions/17B_learning_curve_alpha.py
十八、深入:决策树与森林
在这里,我们将探索一类基于决策树的算法。 最基本决策树非常直观。 它们编码一系列if和else选项,类似于一个人如何做出决定。 但是,从数据中完全可以了解要问的问题以及如何处理每个答案。
例如,如果你想创建一个识别自然界中发现的动物的指南,你可能会问以下一系列问题:
- 动物是大于还是小于一米?
- 较大:动物有角吗?
- 是的:角长是否超过十厘米?
- 不是:动物有项圈吗?
- 较大:动物有角吗?
- 较小:动物有两条腿还是四条腿?
- 二:动物有翅膀吗?
- 四:动物有浓密的尾巴吗?
等等。 这种问题的二元分裂是决策树的本质。
基于树的模型的主要好处之一是它们几乎不需要数据预处理。 它们可以处理不同类型的变量(连续和离散),并且对特征的缩放不变。
另一个好处是基于树的模型被称为“非参数”,这意味着他们没有一套固定的参数需要学习。 相反,如果给出更多数据,树模型可以变得越来越灵活。 换句话说,自由参数的数量随着样本量而增长并且不是固定的,例如在线性模型中。
决策树回归
决策树是一种简单的二元分类树,类似于最近邻分类。 它可以这样使用:
from figures import make_dataset
x, y = make_dataset()
X = x.reshape(-1, 1)
plt.figure()
plt.xlabel('Feature X')
plt.ylabel('Target y')
plt.scatter(X, y);
from sklearn.tree import DecisionTreeRegressor
reg = DecisionTreeRegressor(max_depth=5)
reg.fit(X, y)
X_fit = np.linspace(-3, 3, 1000).reshape((-1, 1))
y_fit_1 = reg.predict(X_fit)
plt.figure()
plt.plot(X_fit.ravel(), y_fit_1, color='tab:blue', label="prediction")
plt.plot(X.ravel(), y, 'C7.', label="training data")
plt.legend(loc="best");
单个决策树允许我们以非参数方式估计标签,但显然存在一些问题。 在某些地区,该模型表现出高偏差并且对数据欠拟合。 (请见不遵循数据轮廓的长扁形线条),而在其他区域,模型表现高方差并且过拟合数据(反映为受单点噪声影响的窄峰形)。
决策树分类
决策树分类原理非常相似,通过将叶子中的多数类分配给叶子中的所有点:
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from figures import plot_2d_separator
from figures import cm2
X, y = make_blobs(centers=[[0, 0], [1, 1]], random_state=61526, n_samples=100)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
clf = DecisionTreeClassifier(max_depth=5)
clf.fit(X_train, y_train)
plt.figure()
plot_2d_separator(clf, X, fill=True)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm2, s=60, alpha=.7, edgecolor='k')
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm2, s=60, edgecolor='k');
有许多参数可以控制树的复杂性,但最容易理解的是最大深度。这限制了树可以对输入空间进行划分的精确度,或者在决定样本所在的类之前,可以询问多少if-else问题。
此参数对于调整树和基于树的模型非常重要。下面的交互式图表显示了该模型的欠拟合和过拟合。 max_depth为 1 显然是一个欠拟合的模型,而 7 或 8 的深度明显过拟合。对于该数据集,树可以生长的最大深度是 8,此时每个叶仅包含来自单个类的样本。这被称为所有叶子都是“纯的”。
在下面的交互式图中,区域被指定为蓝色和红色,来表明该区域的预测类。颜色的阴影表示该类的预测概率(较暗为较高概率),而黄色区域表示任一类的预测概率相等。
from figures import plot_tree
max_depth = 3
plot_tree(max_depth=max_depth)
决策树训练快,易于理解,并且经常产生可解释的模型。 但是,单个树通常倾向于过拟合训练数据。 使用上面的滑块,你可能会注意到,即使在类之间有良好的分隔之前,模型也会开始过拟合。
因此,在实践中,更常见的是组合多个树来产生更好泛化的模型。 组合树的最常用方法是随机森林和梯度提升树。
随机森林
随机森林只是许多树,建立在数据的不同随机子集(带放回抽样)上,并对于每个分裂,使用特征的不同随机子集(无放回抽样)。 这使得树彼此不同,并使它们过拟合不同的方面。 然后,他们的预测被平均,产生更平稳的估计,更少过拟合。
from figures import plot_forest
max_depth = 3
plot_forest(max_depth=max_depth)
通过交叉验证选择最优估计
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_digits
from sklearn.ensemble import RandomForestClassifier
digits = load_digits()
X, y = digits.data, digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
rf = RandomForestClassifier(n_estimators=200)
parameters = {'max_features':['sqrt', 'log2', 10],
'max_depth':[5, 7, 9]}
clf_grid = GridSearchCV(rf, parameters, n_jobs=-1)
clf_grid.fit(X_train, y_train)
clf_grid.score(X_train, y_train)
clf_grid.score(X_test, y_test)
另一个选项:梯度提升
可能有用的另一种集合方法是提升:在这里,我们构建了一个由 200 个估计器组成的链,它迭代地改进了先前估计器的结果,而不是查看(比方说)200 个并行估计器。 我们的想法是,通过顺序应用非常快速,简单的模型,我们可以获得比任何单个部分更好的总模型误差。
from sklearn.ensemble import GradientBoostingRegressor
clf = GradientBoostingRegressor(n_estimators=100, max_depth=5, learning_rate=.2)
clf.fit(X_train, y_train)
print(clf.score(X_train, y_train))
print(clf.score(X_test, y_test))
练习:梯度提升的交叉验证
使用网格搜索在数字数据集上优化梯度提升树
learning_rate和max_depth。
from sklearn.datasets import load_digits
from sklearn.ensemble import GradientBoostingClassifier
digits = load_digits()
X_digits, y_digits = digits.data, digits.target
# split the dataset, apply grid-search
# %load solutions/18_gbc_grid.py
特征的重要性
RandomForest和GradientBoosting对象在拟合之后都会提供feature_importances_属性。 此属性是这些模型最强大的功能之一。 它们基本上量化了在不同树的节点中,每个特征对表现的贡献程度。
X, y = X_digits[y_digits < 2], y_digits[y_digits < 2]
rf = RandomForestClassifier(n_estimators=300, n_jobs=1)
rf.fit(X, y)
print(rf.feature_importances_) # one value per feature
plt.figure()
plt.imshow(rf.feature_importances_.reshape(8, 8), cmap=plt.cm.viridis, interpolation='nearest')
十九、自动特征选择
我们经常收集许多可能与监督预测任务相关的特征,但我们不知道它们中的哪一个实际上是预测性的。 为了提高可解释性,有时还提高泛化表现,我们可以使用自动特征选择来选择原始特征的子集。 有几种可用的特征选择方法,我们将按照复杂性的升序来解释。
对于给定的监督模型,最佳特征选择策略是尝试每个可能的特征子集,并使用该子集评估泛化表现。 但是,特征子集是指数级,因此这种详尽的搜索通常是不可行的。 下面讨论的策略可以被认为是这种不可行计算的替代。
单变量统计
选择要素的最简单方法是使用单变量统计,即通过单独查看每个特征并运行统计检验,来查看它是否与目标相关。 这种检验也称为方差分析(ANOVA)。
我们创建了一个人造数据集,其中包含乳腺癌数据和另外 50 个完全随机的特征。
from sklearn.datasets import load_breast_cancer, load_digits
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
# get deterministic random numbers
rng = np.random.RandomState(42)
noise = rng.normal(size=(len(cancer.data), 50))
# add noise features to the data
# the first 30 features are from the dataset, the next 50 are noise
X_w_noise = np.hstack([cancer.data, noise])
X_train, X_test, y_train, y_test = train_test_split(X_w_noise, cancer.target,
random_state=0, test_size=.5)
我们必须在统计检验的 p 值上定义一个阈值,来决定要保留多少特征。 在 scikit-learn 中实现了几种策略,一种直接的策略是SelectPercentile,它选择原始特征的百分位数(下面我们选择 50%):
from sklearn.feature_selection import SelectPercentile
# use f_classif (the default) and SelectPercentile to select 50% of features:
select = SelectPercentile(percentile=50)
select.fit(X_train, y_train)
# transform training set:
X_train_selected = select.transform(X_train)
print(X_train.shape)
print(X_train_selected.shape)
我们还可以直接使用检验统计量,来查看每个特征的相关性。 由于乳腺癌数据集是一项分类任务,我们使用f_classif,F 检验用于分类。 下面我们绘制 p 值,与 80 个特征中的每一个相关(30 个原始特征和 50 个噪声特征)。 低 p 值表示信息性特征。
from sklearn.feature_selection import f_classif, f_regression, chi2
F, p = f_classif(X_train, y_train)
plt.figure()
plt.plot(p, 'o')
显然,前 30 个特征中的大多数具有非常小的 p 值。
回到SelectPercentile转换器,我们可以使用get_support方法获得所选特征:
mask = select.get_support()
print(mask)
# 展示掩码。黑色是真,白色是假
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
几乎所有最初的 30 个特征都被还原了。 我们还可以通过在数据上训练监督模型,来分析特征选择的效果。 仅在训练集上学习特征选择非常重要!
from sklearn.linear_model import LogisticRegression
# 转换测试数据
X_test_selected = select.transform(X_test)
lr = LogisticRegression()
lr.fit(X_train, y_train)
print("Score with all features: %f" % lr.score(X_test, y_test))
lr.fit(X_train_selected, y_train)
print("Score with only selected features: %f" % lr.score(X_test_selected, y_test))
基于模型的特征选择
用于特征选择的稍微复杂的方法,是使用监督机器学习模型,并基于模型认为它们的重要性来选择特征。 这要求模型提供某种方法,按重要性对特征进行排名。 这适用于所有基于树的模型(实现get_feature_importances)和所有线性模型,系数可用于确定特征对结果的影响程度。
任何这些模型都可以制作成变换器,通过使用SelectFromModel类包装它,用于特征选择:
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier
select = SelectFromModel(RandomForestClassifier(n_estimators=100, random_state=42), threshold="median")
select.fit(X_train, y_train)
X_train_rf = select.transform(X_train)
print(X_train.shape)
print(X_train_rf.shape)
mask = select.get_support()
# 展示掩码。黑色是真,白色是假
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
X_test_rf = select.transform(X_test)
LogisticRegression().fit(X_train_rf, y_train).score(X_test_rf, y_test)
此方法构建单个模型(在本例中为随机森林)并使用此模型中的特征重要性。 我们可以通过在数据子集上训练多个模型,来进行更精细的搜索。 一种特殊的策略是递归特征消除:
递归特征消除
递归特征消除在整个特征集上构建模型,类似于上述方法,选择模型认为最重要的特征子集。 但是,通常只会从数据集中删除单个要素,并使用其余要素构建新模型。 重复删除特征和模型构建的过程,直到只剩下预定数量的特征:
from sklearn.feature_selection import RFE
select = RFE(RandomForestClassifier(n_estimators=100, random_state=42), n_features_to_select=40)
select.fit(X_train, y_train)
# 可视化所选特征
mask = select.get_support()
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
X_train_rfe = select.transform(X_train)
X_test_rfe = select.transform(X_test)
LogisticRegression().fit(X_train_rfe, y_train).score(X_test_rfe, y_test)
select.score(X_test, y_test)
练习
创建“XOR”数据集,如下面的第一个单元格:
添加随机特征,并使用随机森林,在还原原始特征时,比较单变量选择与基于模型的选择。
import numpy as np
rng = np.random.RandomState(1)
# 在 [0,1] 范围内生成 400 个随机整数
X = rng.randint(0, 2, (200, 2))
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0) # XOR creation
plt.scatter(X[:, 0], X[:, 1], c=plt.cm.tab10(y))
# %load solutions/19_univariate_vs_mb_selection.py
二十、无监督学习:层次和基于密度的聚类算法
在第八章中,我们介绍了一种必不可少且广泛使用的聚类算法 K-means。 K-means 的一个优点是它非常容易实现,并且与其他聚类算法相比,它在计算上也非常有效。 然而,我们已经看到 K-Means 的一个缺点是它只有在数据可以分组为球形时才能正常工作。 此外,我们必须事先指定簇的数量k - 如果我们没有我们期望找到多少个簇的先验知识,这可能是一个问题。
在本笔记本中,我们将介绍两种可选的聚类方法,层次聚类和基于密度的聚类。
层次聚类
层次聚类的一个很好的特性是,我们可以将结果可视化为树状图,即层次树。 使用可视化,我们可以通过设置“深度”阈值来决定我们希望数据集的簇有多“深”。 或者换句话说,我们不需要预先决定簇的数量。
聚合和分裂的层次聚类
此外,我们可以区分两种主要的层次聚类方法:分裂聚类和聚合聚类。 在聚合聚类中,我们从数据集中的单个样本开始,并迭代地将其与其他样本合并以形成簇 - 我们可以将其视为构建簇的树状图的自底向上的方法。
然而,在分裂聚类中,我们从作为一个簇的整个数据集开始,并且我们迭代地将其拆分成更小的子簇 - 自顶向下的方法。
在这个笔记本中,我们将使用聚合聚类。
单个和完整链接
现在,下一个问题是我们如何测量样本之间的相似性。 一种方法是我们已经在 K-Means 算法中使用的,熟悉的欧几里德距离度量。 作为回顾,两个m维向量p和q之间的距离可以计算为:
然而,这是两个个样本之间的距离。 现在,我们如何计算样本子集之间的相似性,以便在构建树状图时决定合并哪些簇? 即,我们的目标是迭代地合并最相似的一对簇,直到只剩下一个大簇。 有许多不同的方法,例如单个和完整链接。
在单个链接中,我们在每两个簇中选取一对最相似的样本(例如,基于欧几里德距离),并将具有最相似的两个成员的两个簇合并为一个新的更大的簇。
在完整链接中,我们比较每两个簇的两个最不相似的成员,并且我们合并两个簇,其中两个最不相似的成员之间的距离最小。
译者注:还有比较两个簇形心的方法,算是一种折中。
为了看到实际的聚合层次聚类方法,让我们加载熟悉的鸢尾花数据集 - 我们假装不知道真正的类标签,并想要找出它包含多少不同的物种:
from sklearn.datasets import load_iris
from figures import cm3
iris = load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
n_samples, n_features = X.shape
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cm3)
首先,我们从一些探索性聚类开始,使用 SciPy 的linkage和dendrogram函数来可视化簇的树状图:
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
clusters = linkage(X,
metric='euclidean',
method='complete')
dendr = dendrogram(clusters)
plt.ylabel('Euclidean Distance')
接下来,让我们使用来自 scikit-learn 的AgglomerativeClustering估计器,并将数据集划分为 3 个簇。你能猜出它会重现的树状图中有哪 3 个簇吗?
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3,
affinity='euclidean',
linkage='complete')
prediction = ac.fit_predict(X)
print('Cluster labels: %s\n' % prediction)
plt.scatter(X[:, 0], X[:, 1], c=prediction, cmap=cm3)
基于密度的聚类 - DBSCAN
另一种有用的聚类方法是“具有噪声的基于密度的聚类方法”(DBSCAN)。 本质上,我们可以将 DBSCAN 视为一种算法,该算法根据密集的点区域将数据集划分为子分组。
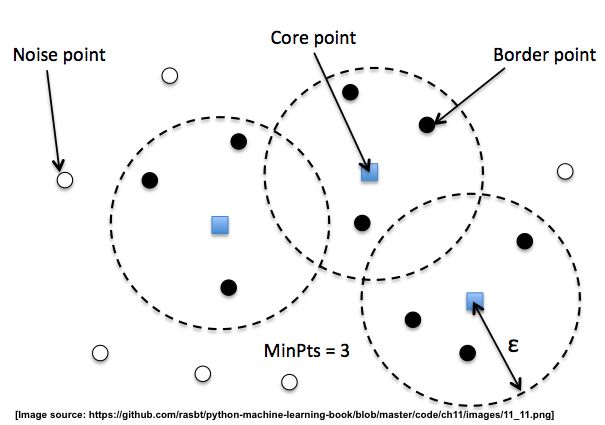
在 DBSCAN 中,我们区分了 3 种不同的“点”:
- 核心点:核心点是一个点,在其半径
epsilon内,至少具有最小数量(MinPts)的其他点。 - 边界点:边界点是一个点,它不是核心点,因为它的邻域中没有足够的
MinPts,但位于核心点的半径epsilon内。 - 噪点:所有其他的点,既不是核心点也不是边界点。
DBSCAN 的一个很好的特性是我们不必预先指定多少个簇。 但是,它需要设置其他超参数,例如MinPts的值和半径epsilon。
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=400,
noise=0.1,
random_state=1)
plt.scatter(X[:,0], X[:,1])
plt.show()
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2,
min_samples=10,
metric='euclidean')
prediction = db.fit_predict(X)
print("Predicted labels:\n", prediction)
plt.scatter(X[:, 0], X[:, 1], c=prediction, cmap=cm3)
练习
使用以下玩具数据集,两个同心圆,尝试我们到目前为止使用的三种不同的聚类算法:
KMeans,AgglomerativeClustering和DBSCAN。 哪种聚类算法能够最好地再现或发现隐藏的结构(假装我们不知道y)? 你能解释为什么这个特殊的算法是一个不错的选择,而另外两个“失败”了?
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1500,
factor=.4,
noise=.05)
plt.scatter(X[:, 0], X[:, 1], c=y);
# %load solutions/20_clustering_comparison.py
二十一、无监督学习:非线性降维
流形学习
PCA 的一个弱点是它无法检测到非线性特征。 已经开发了一组称为流形学习的算法,来解决这个缺陷。流形学习中使用的规范数据集是 S 曲线:
from sklearn.datasets import make_s_curve
X, y = make_s_curve(n_samples=1000)
from mpl_toolkits.mplot3d import Axes3D
ax = plt.axes(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], X[:, 2], c=y)
ax.view_init(10, -60);
这是一个嵌入三维的二维数据集,但它以某种方式嵌入,PCA 无法发现底层数据方向:
from sklearn.decomposition import PCA
X_pca = PCA(n_components=2).fit_transform(X)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y);
然而,sklearn.manifold子模块中可用的流形学习算法能够还原底层的二维流形:
from sklearn.manifold import Isomap
iso = Isomap(n_neighbors=15, n_components=2)
X_iso = iso.fit_transform(X)
plt.scatter(X_iso[:, 0], X_iso[:, 1], c=y);
数字数据上的流形学习
我们可以将流形学习技术应用于更高维度的数据集,例如我们之前看到的数字数据:
from sklearn.datasets import load_digits
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5),
subplot_kw={'xticks':(), 'yticks': ()})
for ax, img in zip(axes.ravel(), digits.images):
ax.imshow(img, interpolation="none", cmap="gray")
我们可以使用线性技术(例如 PCA)可视化数据集。 我们看到这已经提供了一些数据的直觉:
# 构建 PCA 模型
pca = PCA(n_components=2)
pca.fit(digits.data)
# 将数字数据转换为前两个主成分
digits_pca = pca.transform(digits.data)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525",
"#A83683", "#4E655E", "#853541", "#3A3120","#535D8E"]
plt.figure(figsize=(10, 10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max() + 1)
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max() + 1)
for i in range(len(digits.data)):
# 实际上将数字绘制为文本而不是使用散点图
plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("first principal component")
plt.ylabel("second principal component");
但是,使用更强大的非线性技术可以提供更好的可视化效果。 在这里,我们使用 t-SNE 流形学习方法:
from sklearn.manifold import TSNE
tsne = TSNE(random_state=42)
# 使用 fit_transform 而不是 fit,因为 TSNE 没有 fit 方法
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
# 实际上将数字绘制为文本而不是使用散点图
plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
t-SNE 比其他流形学习算法运行时间更长,但结果非常惊人。 请记住,此算法纯粹是无监督的,并且不知道类标签。 它仍然能够很好地分离类别(尽管类 4 和 类 9 已被分成多个分组)。
练习
将 isomap 应用于数字数据集的结果与 PCA 和 t-SNE 的结果进行比较。 你认为哪个结果看起来最好?
鉴于 t-SNE 很好地将类别分开,人们可能会试图将这个处理过程用于分类。 尝试在使用 t-SNE 转换的数字数据上,训练 K 最近邻分类器,并与没有任何转换的数据集上的准确性比较。
# %load solutions/21A_isomap_digits.py
# %load solutions/21B_tsne_classification.py
二十二、无监督学习:异常检测
常检测是一种机器学习任务,包括发现所谓的异常值。
“异常值是一种数据集中的观测值,似乎与该组数据的其余部分不一致。”-- Johnson 1992
“异常值是一种观测值,与其他观测值有很大差异,引起人们怀疑它是由不同的机制产生的。”-- Outlier/Anomaly Hawkins 1980
异常检测设定的类型
- 监督 AD
- 标签可用于正常和异常数据
- 类似于稀有类挖掘/不平衡分类
- 半监督 AD(新奇检测)
- 只有正常的数据可供训练
- 该算法仅学习正常数据
- 无监督 AD(异常值检测)
- 没有标签,训练集 = 正常 + 异常数据
- 假设:异常非常罕见
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
让我们首先熟悉不同的无监督异常检测方法和算法。 为了可视化不同算法的输出,我们考虑包含二维高斯混合的玩具数据集。
生成数据集
from sklearn.datasets import make_blobs
X, y = make_blobs(n_features=2, centers=3, n_samples=500,
random_state=42)
X.shape
plt.figure()
plt.scatter(X[:, 0], X[:, 1])
plt.show()
使用密度估计的异常检测
from sklearn.neighbors.kde import KernelDensity
# 用高斯核密度估计器估算密度
kde = KernelDensity(kernel='gaussian')
kde = kde.fit(X)
kde
kde_X = kde.score_samples(X)
print(kde_X.shape) # 包含数据的对数似然。 越小样本越罕见
from scipy.stats.mstats import mquantiles
alpha_set = 0.95
tau_kde = mquantiles(kde_X, 1. - alpha_set)
n_samples, n_features = X.shape
X_range = np.zeros((n_features, 2))
X_range[:, 0] = np.min(X, axis=0) - 1.
X_range[:, 1] = np.max(X, axis=0) + 1.
h = 0.1 # step size of the mesh
x_min, x_max = X_range[0]
y_min, y_max = X_range[1]
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
grid = np.c_[xx.ravel(), yy.ravel()]
Z_kde = kde.score_samples(grid)
Z_kde = Z_kde.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_kde, levels=tau_kde, colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={tau_kde[0]: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.show()
单类 SVM
基于密度的估计的问题在于,当数据的维数增加时,它们往往变得低效。 这就是所谓的维度灾难,尤其会影响密度估算算法。 在这种情况下可以使用单类 SVM 算法。
from sklearn.svm import OneClassSVM
nu = 0.05 # theory says it should be an upper bound of the fraction of outliers
ocsvm = OneClassSVM(kernel='rbf', gamma=0.05, nu=nu)
ocsvm.fit(X)
X_outliers = X[ocsvm.predict(X) == -1]
Z_ocsvm = ocsvm.decision_function(grid)
Z_ocsvm = Z_ocsvm.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_ocsvm, levels=[0], colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={0: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_outliers[:, 0], X_outliers[:, 1], color='red')
plt.show()
支持向量 - 离群点
所谓的单类 SVM 的支持向量形成离群点。
X_SV = X[ocsvm.support_]
n_SV = len(X_SV)
n_outliers = len(X_outliers)
print('{0:.2f} <= {1:.2f} <= {2:.2f}?'.format(1./n_samples*n_outliers, nu, 1./n_samples*n_SV))
只有支持向量涉及单类 SVM 的决策函数。
- 绘制单类 SVM 决策函数的级别集,就像我们对真实密度所做的那样。
- 突出支持向量。
plt.figure()
plt.contourf(xx, yy, Z_ocsvm, 10, cmap=plt.cm.Blues_r)
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.scatter(X_SV[:, 0], X_SV[:, 1], color='orange')
plt.show()
练习
更改`gamma``参数并查看它对决策函数平滑度的影响。
# %load solutions/22_A-anomaly_ocsvm_gamma.py
隔离森林
隔离森林是一种基于树的异常检测算法。 该算法构建了许多随机树,其基本原理是,如果样本被隔离,在非常少量的随机分割之后,它应该单独存在于叶子中。 隔离森林根据样本最终所在的树的深度建立异常得分。
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(n_estimators=300, contamination=0.10)
iforest = iforest.fit(X)
Z_iforest = iforest.decision_function(grid)
Z_iforest = Z_iforest.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_iforest,
levels=[iforest.threshold_],
colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15,
fmt={iforest.threshold_: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.show()
练习
以图形方式说明树的数量对决策函数平滑度的影响。
# %load solutions/22_B-anomaly_iforest_n_trees.py
数字数据集上的图解
我们现在将应用IsolationForest算法来查找以非常规方式编写的数字。
from sklearn.datasets import load_digits
digits = load_digits()
数字数据集包括8×8的数字图像。
images = digits.images
labels = digits.target
images.shape
i = 102
plt.figure(figsize=(2, 2))
plt.title('{0}'.format(labels[i]))
plt.axis('off')
plt.imshow(images[i], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
要将图像用作训练集,我们需要将图像展开。
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
data.shape
X = data
y = digits.target
X.shape
让我们关注数字 5。
X_5 = X[y == 5]
X_5.shape
fig, axes = plt.subplots(1, 5, figsize=(10, 4))
for ax, x in zip(axes, X_5[:5]):
img = x.reshape(8, 8)
ax.imshow(img, cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
- 让我们使用
IsolationForest来查找前 5% 最异常的图像。 - 让我们绘制他们吧!
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(contamination=0.05)
iforest = iforest.fit(X_5)
使用iforest.decision_function计算“异常”的级别。越低就越异常。
iforest_X = iforest.decision_function(X_5)
plt.hist(iforest_X);
让我们绘制最强的正常值。
X_strong_inliers = X_5[np.argsort(iforest_X)[-10:]]
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
for i, ax in zip(range(len(X_strong_inliers)), axes.ravel()):
ax.imshow(X_strong_inliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
让我们绘制最强的异常值。
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
X_outliers = X_5[iforest.predict(X_5) == -1]
for i, ax in zip(range(len(X_outliers)), axes.ravel()):
ax.imshow(X_outliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
练习
用所有其他数字重新运行相同的分析。
# %load solutions/22_C-anomaly_digits.py
二十三、核外学习 - 用于语义分析的大规模文本分类
可扩展性问题
sklearn.feature_extraction.text.CountVectorizer和sklearn.feature_extraction.text.TfidfVectorizer类受到许多可伸缩性问题的困扰,这些问题都源于vocabulary_属性(Python 字典)的内部使用,它用于将 unicode 字符串特征名称映射为整数特征索引。
主要的可扩展性问题是:
- 文本向量化程序的内存使用情况:所有特征的字符串表示形式都加载到内存中
- 文本特征提取的并行化问题:
vocabulary_是一个共享状态:复杂的同步和开销 - 不可能进行在线或核外/流式学习:
vocabulary_需要从数据中学习:在遍历一次整个数据集之前无法知道其大小
为了更好地理解这个问题,让我们看一下vocabulary_属性的工作原理。 在fit的时候,语料库的标记由整数索引唯一标识,并且该映射存储在词汇表中:
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(min_df=1)
vectorizer.fit([
"The cat sat on the mat.",
])
vectorizer.vocabulary_
在transform的时候,使用词汇表来构建出现矩阵:
X = vectorizer.transform([
"The cat sat on the mat.",
"This cat is a nice cat.",
]).toarray()
print(len(vectorizer.vocabulary_))
print(vectorizer.get_feature_names())
print(X)
让我们用稍大的语料库重新拟合:
vectorizer = CountVectorizer(min_df=1)
vectorizer.fit([
"The cat sat on the mat.",
"The quick brown fox jumps over the lazy dog.",
])
vectorizer.vocabulary_
vocabulary_随着训练语料库的大小而(以对数方式)增长。 请注意,我们无法在 2 个文本文档上并行构建词汇表,因为它们共享一些单词,因此需要某种共享数据结构或同步障碍,这对于设定来说很复杂,特别是如果我们想要将处理过程分发给集群的时候。
有了这个新的词汇表,输出空间的维度现在变大了:
X = vectorizer.transform([
"The cat sat on the mat.",
"This cat is a nice cat.",
]).toarray()
print(len(vectorizer.vocabulary_))
print(vectorizer.get_feature_names())
print(X)
IMDB 电影数据集
为了说明基于词汇的向量化器的可扩展性问题,让我们为经典文本分类任务加载更真实的数据集:文本文档的情感分析。目标是从互联网电影数据库(IMDb)中区分出积极的电影评论。
在接下来的章节中,使用了 Maas 等人收集的来自 IMDb 的电影评论的大型子集。
A. L. Maas, R. E. Daly, P. T. Pham, D. Huang, A. Y. Ng, and C. Potts. Learning Word Vectors for Sentiment Analysis. In the proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 142–150, Portland, Oregon, USA, June 2011. Association for Computational Linguistics.
该数据集包含 50,000 个电影评论,分为 25,000 个培训样本和 25,000 个测试样本。评论标记为负面(neg)或正面(pos)。此外,正面意味着电影在 IMDb 上收到> 6星;负面意味着电影收到<5星。
假设../fetch_data.py脚本成功运行,以下文件应该可用:
import os
train_path = os.path.join('datasets', 'IMDb', 'aclImdb', 'train')
test_path = os.path.join('datasets', 'IMDb', 'aclImdb', 'test')
现在,让我们通过 scikit-learn 的load_files函数,将它们加载到我们的活动会话中:
from sklearn.datasets import load_files
train = load_files(container_path=(train_path),
categories=['pos', 'neg'])
test = load_files(container_path=(test_path),
categories=['pos', 'neg'])
注
由于电影数据集由 50,000 个单独的文本文件组成,因此执行上面的代码片段可能需要约 20 秒或更长时间。
load_files函数将数据集加载到sklearn.datasets.base.Bunch对象中,这些对象是 Python 字典:
train.keys()
特别是,我们只对data和target数组感兴趣。
import numpy as np
for label, data in zip(('TRAINING', 'TEST'), (train, test)):
print('\n\n%s' % label)
print('Number of documents:', len(data['data']))
print('\n1st document:\n', data['data'][0])
print('\n1st label:', data['target'][0])
print('\nClass names:', data['target_names'])
print('Class count:',
np.unique(data['target']), ' -> ',
np.bincount(data['target']))
正如我们在上面所看到的,target数组由整数 0 和 1 组成,其中 0 代表负面,1 代表正面。
哈希技巧
回忆一下,使用基于词汇表的向量化器的词袋表示:
要解决基于词汇表的向量化器的局限性,可以使用散列技巧。 我们可以使用散列函数和模运算,而不是在 Python 字典中构建和存储特征名称到特征索引的显式映射:
对于哈希技巧的原始论文的更多信息和参考,请见以下网站,以及特定于语言的描述请见这里。
from sklearn.utils.murmurhash import murmurhash3_bytes_u32
# encode for python 3 compatibility
for word in "the cat sat on the mat".encode("utf-8").split():
print("{0} => {1}".format(
word, murmurhash3_bytes_u32(word, 0) % 2 ** 20))
这种映射完全是无状态的,并且输出空间的维度预先明确固定(这里我们使用2 ** 20的模,这意味着大约 1M 的维度)。 这使得有可能解决基于词汇表的向量化器的局限性,既可用于并行化,也可用于在线/核外学习。
HashingVectorizer类是CountVectorizer(或use_idf=False的TfidfVectorizer类)的替代品,它在内部使用 murmurhash 哈希函数:
from sklearn.feature_extraction.text import HashingVectorizer
h_vectorizer = HashingVectorizer(encoding='latin-1')
h_vectorizer
它共享相同的“预处理器”,“分词器”和“分析器”基础结构:
analyzer = h_vectorizer.build_analyzer()
analyzer('This is a test sentence.')
我们可以将数据集向量化为scipy稀疏矩阵,就像我们使用CountVectorizer或TfidfVectorizer一样,除了我们可以直接调用transform方法:没有必要拟合,因为HashingVectorizer是无状态变换器:
docs_train, y_train = train['data'], train['target']
docs_valid, y_valid = test['data'][:12500], test['target'][:12500]
docs_test, y_test = test['data'][12500:], test['target'][12500:]
默认情况下,输出的维度事先固定为n_features = 2 ** 20(接近 1M 个特征),来最大限度地减少大多数分类问题的碰撞率,同时具有合理大小的线性模型(coef_属性中的 1M 权重):
h_vectorizer.transform(docs_train)
现在,让我们将HashingVectorizer的计算效率与CountVectorizer进行比较:
h_vec = HashingVectorizer(encoding='latin-1')
%timeit -n 1 -r 3 h_vec.fit(docs_train, y_train)
count_vec = CountVectorizer(encoding='latin-1')
%timeit -n 1 -r 3 count_vec.fit(docs_train, y_train)
我们可以看到,在这种情况下,HashingVectorizer比Countvectorizer快得多。
最后,让我们在 IMDb 训练子集上训练一个LogisticRegression分类器:
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
h_pipeline = Pipeline([
('vec', HashingVectorizer(encoding='latin-1')),
('clf', LogisticRegression(random_state=1)),
])
h_pipeline.fit(docs_train, y_train)
print('Train accuracy', h_pipeline.score(docs_train, y_train))
print('Validation accuracy', h_pipeline.score(docs_valid, y_valid))
import gc
del count_vec
del h_pipeline
gc.collect()
核外学习
核外学习是在不放不进内存或 RAM 的数据集上训练机器学习模型的任务。 这需要以下条件:
具有固定输出维度的特征提取层
提前知道所有类别的列表(在这种情况下,我们只有正面和负面的评论)
支持增量学习的机器学习算法(scikit-learn 中的partial_fit方法)。
在以下部分中,我们将建立一个简单的批量训练函数来迭代地训练SGDClassifier。
但首先,让我们将文件名加载到 Python 列表中:
train_path = os.path.join('datasets', 'IMDb', 'aclImdb', 'train')
train_pos = os.path.join(train_path, 'pos')
train_neg = os.path.join(train_path, 'neg')
fnames = [os.path.join(train_pos, f) for f in os.listdir(train_pos)] +\
[os.path.join(train_neg, f) for f in os.listdir(train_neg)]
fnames[:3]
接下来,让我们创建目标标签数组:
y_train = np.zeros((len(fnames), ), dtype=int)
y_train[:12500] = 1
np.bincount(y_train)
现在,我们实现batch_train函数,如下所示:
from sklearn.base import clone
def batch_train(clf, fnames, labels, iterations=25, batchsize=1000, random_seed=1):
vec = HashingVectorizer(encoding='latin-1')
idx = np.arange(labels.shape[0])
c_clf = clone(clf)
rng = np.random.RandomState(seed=random_seed)
for i in range(iterations):
rnd_idx = rng.choice(idx, size=batchsize)
documents = []
for i in rnd_idx:
with open(fnames[i], 'r', encoding='latin-1') as f:
documents.append(f.read())
X_batch = vec.transform(documents)
batch_labels = labels[rnd_idx]
c_clf.partial_fit(X=X_batch,
y=batch_labels,
classes=[0, 1])
return c_clf
请注意,我们没有像上一节中那样使用LogisticRegression,但我们将使用具有 logistic 成本函数的SGDClassifier。 SGD代表随机梯度下降,这是一种优化算法,它逐样本迭代地优化权重系数,这允许我们一块一块地将数据馈送给分类器。
我们训练SGDClassifier;使用batch_train函数的默认设置,它将在25 * 1000 = 25000个文档上训练分类器。 (根据你的机器,这可能需要>2分钟)
from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier(loss='log', random_state=1, max_iter=1000)
sgd = batch_train(clf=sgd,
fnames=fnames,
labels=y_train)
最后,让我们评估一下它的表现:
vec = HashingVectorizer(encoding='latin-1')
sgd.score(vec.transform(docs_test), y_test)
哈希向量化器的限制
使用Hashing Vectorizer可以实现流式和并行文本分类,但也可能会引入一些问题:
- 碰撞会在数据中引入太多噪声并降低预测质量,
HashingVectorizer不提供“反向文档频率”重新加权(缺少use_idf=True选项)。- 没有反转映射,和从特征索引中查找特征名称的简单方法。
- 可以通过增加
n_features参数来控制冲突问题。
可以通过在向量化器的输出上附加TfidfTransformer实例来重新引入 IDF 加权。然而,用于特征重新加权的idf_统计量的计算,需要在能够开始训练分类器之前,额外遍历训练集至少一次:这打破了在线学习方案。
缺少逆映射(TfidfVectorizer的get_feature_names()方法)更难以解决。这将需要扩展HashingVectorizer类来添加“跟踪”模式,来记录最重要特征的映射,来提供统计调试信息。
在调试特征提取问题的同时,建议在数据集的小型子集上使用TfidfVectorizer(use_idf=False),来模拟具有get_feature_names()方法且没有冲突问题的HashingVectorizer()实例。
练习
在我们上面的
batch_train函数的实现中,我们在每次迭代中随机抽取k个训练样本作为批量,这可以被视为带放回的随机子采样。 你可以修改batch_train函数,使它无放回地迭代文档,即它在每次迭代中使用每个文档一次。
# %load solutions/23_batchtrain.py