哈夫曼树(Huffman-Tree)的构造及应用
本文以学习笔记的性质谈一谈哈夫曼树较为严谨的贪心做法。
哈夫曼树的构造
有这样一棵k叉树,它的叶子节点有权值,第i个叶子节点权值为 wi(wi>0) w i ( w i > 0 ) ,他的深度为 li l i ,要求最小化 ∑wi∗li ∑ w i ∗ l i ,这样问题的解称为k叉哈夫曼树。
为了最小化 ∑wi∗li ∑ w i ∗ l i ,那肯定要让小的数尽量深,那么我们可以想到一个贪心做法:
1、以权值建立一个小根堆,每次堆中取出最小的k个数,记他们的和为q,将q累加进ans中
2、将q重新放入堆中,在树中我们相当于将权值为q的点作为这k个点的父亲
3、把1 2 步骤重复做,直到堆中只剩一个元素(w1+w2+…+wn) 此时的ans就是答案
这里就可以有值得困惑的地方,为什么要这么做呢?
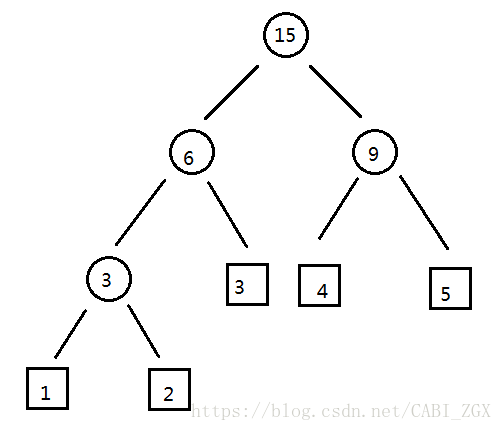
在这一棵树中我们把第4层的的1+2=3加入多叉树作为他们的父亲,那么在计算第3层的时候我们又会把1和2的影响通过3+3=6来累加进ans,相当于把1+2算了两遍,同理在第二层和第一层的计算中我们都会加入1和2的影响,那么最终他们就会被算四次,相当于他们的深度,也就是 ∑wi∗li ∑ w i ∗ l i 。
那么理解了这个之后我们发现这个在k>2的时候是错误的,原因显而易见,当我们的算法进行到最后一步的时候,假如堆内剩余的元素不足k个,也不足以单独作为根(2~k-1)之间,那么第二层的节点就会不足k个,这样的 ∑wi∗li ∑ w i ∗ l i 在n>k(即树的层数>2)的时候绝对不是最小的,因为此刻把任意一个二层以下的节点放到不满的二层ans都会变小。可以画个三叉树理解一下。
那该怎么办呢??我们发现,这个贪心不成立仅当这个树并不是一个满k叉树(是每个非叶子节点都有满k个孩子的那种),所以才有第二层的枝杈不齐的情况,那么我们把他们补成一个满k叉树呢?
没错!我们可以补上一些数使他成为一个满k叉树,那么补什么数呢?我们应该补一个尽量小的数,把叶子节点尽量顶上去(因为下面越少越好),那么因为 wi>0 w i > 0 ,所以我们就补0!
那么我们就在原来贪心算法的基础上,在一开始的堆中加入0直到堆中元素个数 n n 和树的杈数 k k 满足 (n−1)mod(k−1)=0 ( n − 1 ) m o d ( k − 1 ) = 0 。
这个式子可以适用于所有满k叉树的情况。 那么我再来解释一下这个式子如何来,我有一个感性的证明。
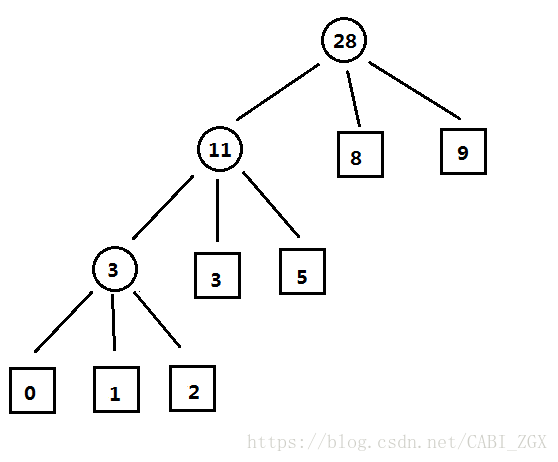
我们以这个树为例,我们想象一下,把这个0的节点代表3这个数提上去,提到第三层,然后在提上去,然后这时候0在第三层,再提上去第二层,最后提上去根。 那么这个0提上去后每层都会有2个(3-1个)孩子,这时候的叶子节点数也少了一个,那么就是(n-1)%(k-1)=0
那么上文提到的贪心算法,在 (n−1)mod(k−1) ( n − 1 ) m o d ( k − 1 ) 的时候为正确,当初始的n不满足这个性质时,我们可以通过补0的方式使得n满足这个性质。 从而在 O(n) O ( n ) 的时间里完成构造。
哈夫曼树的应用
讲完了哈夫曼树的构造,那么接下来,我们通过两道例题来了解哈夫曼树的应用:
合并果子
[NOIP2004]
描述
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有3种果子,数目依次为1,2,9。可以先将1、2堆合并,新堆数目为3,耗费体力为3。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
输入格式
输入包括两行,第一行是一个整数n(1<=n<=10000),表示果子的种类数。第二行包含n个整数,用空格分隔,第i个整数ai(1<=ai<=20000)是第i种果子的数目。
输出格式
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。输入数据保证这个值小于2^31。
思路
因为每次合并需要再次加入影响,我们需要让数量少的果子堆尽量先合并,每次可以合并两堆果子,需要求代价最小。不难发现,这样合并的过程,实际上就是一个二叉哈夫曼树。
那么我们就可以使用上文的贪心算法来求解(不用补0也可以)
code:
#include;
#include荷马史诗
[NOI2015]
描述
追逐影子的人,自己就是影子。 ——荷马
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 n 种不同的单词,从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。Allison 想要用 k 进制串 si 来替换第 i 种单词,使得其满足如下要求:
对于任意的 1≤i,j≤n,i≠j,都有:si 不是 sj 的前缀。
现在 Allison 想要知道,如何选择 si,才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的 si 的最短长度是多少?
一个字符串被称为 k 进制字符串,当且仅当它的每个字符是 0 到 k−1 之间(包括 0 和 k−1)的整数。
字符串 Str1 被称为字符串 Str2 的前缀,当且仅当:存在 1≤t≤m,使得 Str1=Str2[1..t]。其中,m 是字符串 Str2 的长度,Str2[1..t] 表示 Str2 的前 t 个字符组成的字符串。
输入格式
输入文件的第 1 行包含 2 个正整数 n,k,中间用单个空格隔开,表示共有 n 种单词,需要使用 k 进制字符串进行替换。
接下来 n 行,第 i+1 行包含 1 个非负整数 wi,表示第 i 种单词的出现次数。
输出格式
输出文件包括 2 行:
第 1 行输出 1 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 2 行输出 1 个整数,为保证最短总长度的情况下,最长字符串 si 的最短长度。
思路
相对与上一题而言,这题的哈夫曼树的模型就显得比较隐晦。
题目中最重要的一条信息是:
对于任意的 1≤i,j≤n,i≠j,都有:si 不是 sj 的前缀。
那么如果我们把所有的si插进Tire树,如果需要任意的两个单词状态节点互相不为前缀,由Tire性质可以得到所有的单词状态节点都不在非叶子节点(如果他在非叶子节点的话他表示的单词一定是他下面的点表示单词的前缀),那么这样刚好满足了哈夫曼树的性质。
那么k进制的数就代表着一个数会有k个叉(0~k-1),单词的出现次数就可以看作权值,那么我们就把问题转化为了k叉哈夫曼树问题。
这样就可以解决第一问了,但是还有第二问,我们需要让最长的si深度最小,我们只需要在重定义运算符的时候,对于权值相同的点,优先考虑深度较小(合并次数尽量小)的进行合并即可。
code:
#include q;
int main()
{
// freopen("epic.in","r",stdin);
// freopen("epic.ans","w",stdout);
int n,k;scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
ll x;scanf("%lld",&x);
node p; p.val=x; p.dep=1;
q.push(p);
}
if((n-1)%(k-1)!=0)
{
int tt=(n-1)%(k-1);
tt=k-1 - tt; n+=tt;
for(int i=1;i<=tt;i++)
{
node p; p.val=0,p.dep=1;
q.push(p);
}
}
ll ans1=0; int ans2=1;
while(n>1)
{
node tmp; ll sum=0; int mxdp=1;
for(int i=1;i<=k;i++)
{
tmp=q.top(); q.pop();
sum+=tmp.val;
mxdp=max(mxdp,tmp.dep);
}
node p; p.val=sum,p.dep=mxdp+1;
q.push(p);
ans1+=sum;
ans2=max(ans2,mxdp);
n-=k-1;
}
printf("%lld\n%d\n",ans1,ans2);
return 0;
}