集合覆盖问题-基于贪心思想的近似算法-python实现

写这篇主要是想与线性规划求解集合覆盖问题做个性能对比，基于后者的实现方法可参考博文。

本文中数据集X及集族生成规则同上一篇，这里不再介绍。整个贪心算法解决集合覆盖问题的实现代码如下。

# 集合覆盖问题-part1-贪心算法
import time
import random
from itertools import chain
import matplotlib.pyplot as plt

# 生成有限集X
X = set()
iter_ = [100,200, 500]
time_cost = []
for n in iter_:
    start_t = time.clock()
    X = random.sample(range(1, 10000), n)
    print('集合X中元素个数：', len(X))
    print('集合X：', X)

    # 生成子集
    S0 = random.sample(X, 20)
    n1 = random.randint(1, 20)
    x1 = random.randint(1, n1)

    S1 = (random.sample(set(S0), x1))+(random.sample(set(X)-set(S0), n1-x1))
    Sub_set = [S0, S1]

    for item in range(2, n):
        S_item_len = random.randint(1, 20)
        S_last_len = random.randint(1, S_item_len)

        Sub_set_item = list(chain.from_iterable(Sub_set))  # 压平嵌套列表

        if len(set(X) - set(Sub_set_item)) >= S_item_len-S_last_len:
            S_now = (random.sample(set(Sub_set_item), S_last_len))+(random.sample(set(X)-set(Sub_set_item), S_item_len-S_last_len))
            Sub_set.append(S_now)
        else:
            Sub_set.append(list(set(X)-set(Sub_set_item)))
            break
    # print(set(X)-set(list(chain.from_iterable(Sub_set))))  # 检查集合中的元素是否已被子集族全覆盖

    for j in range(n-len(Sub_set)):
        select_num = random.randint(1, 20)
        select_sub = random.sample(X, select_num)
        Sub_set.append(select_sub)
    print('子集族：', Sub_set)

    # 定义函数返回当前子集族中元素个数最多的子集索引
    def max_len_list(sub_list):
        len_sub_list = []
        for i in range(len(sub_list)):
            len_sub_list.append(len(sub_list[i]))
        len_max_list = max(len_sub_list)
        return len_sub_list.index(len_max_list)

    # 贪心算法
    final_set = []
    while len(set(X)) > len(set(list(chain.from_iterable(final_set)))):
        # 返回当前子集族中元素最多的子集，将其加到可行解中
        max_index = max_len_list(Sub_set)
        final_set.append(Sub_set[max_index])

        # 从当前子集族中删掉被加到可行解中的子集
        del Sub_set[max_index]

    print('可行解：', final_set)

    # 记录运行时间
    end_t = time.clock()
    time_iter = end_t-start_t
    print("集合覆盖问题-基于贪心思想运行时间", time_iter)
    time_cost.append(time_iter)
    print('\n')

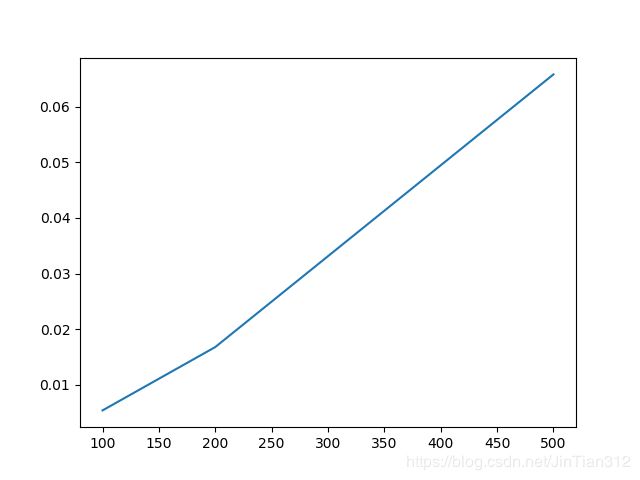
# 可视化
plt.plot(iter_, time_cost)
plt.show()

程序运行结果如下图

可以看出与线性规划求解该问题相比，基于贪心策略的近似算法在性能上有明显提高。